Non-asymptotic Optimal Prediction Error for RKHS-based Partially Functional Linear Models

Under the framework of reproducing kernel Hilbert space (RKHS), we consider the penalized least-squares of the partially functional linear models (PFLM), whose predictor contains both functional and traditional multivariate part, and the multivariate part allows a divergent number of parameters. From the non-asymptotic point of view, we focus on the rate-optimal upper and lower bounds of the prediction error. An exact upper bound for the excess prediction risk is shown in a non-asymptotic form under a more general assumption known as the effective dimension to the model, by which we also show the prediction consistency when the number of multivariate covariates $p$ slightly increases with the sample size $n$. Our new finding implies a trade-off between the number of non-functional predictors and the effective dimension of the kernel principal components to ensure the prediction consistency in the increasing-dimensional setting. The analysis in our proof hinges on the spectral condition of the sandwich operator of the covariance operator and the reproducing kernel, and on the concentration inequalities for the random elements in Hilbert space. Finally, we derive the non-asymptotic minimax lower bound under the regularity assumption of Kullback-Leibler divergence of the models.

Multimodal Image-to-Image Translation via Mutual Information Estimation and Maximization

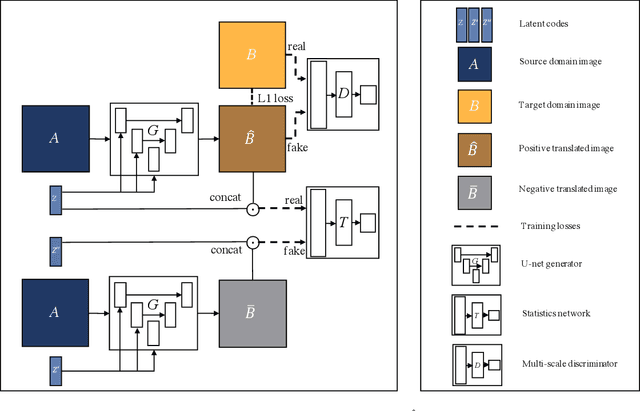
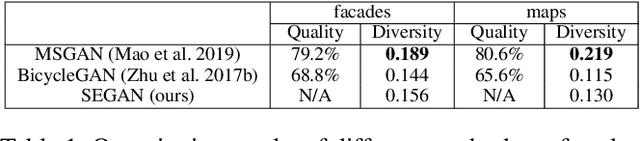
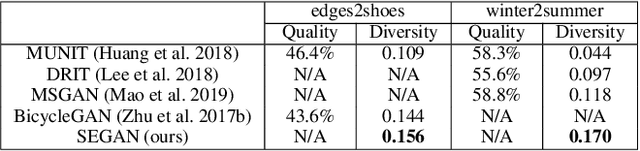
In this paper, we present a novel framework that can achieve multimodal image-to-image translation by simply encouraging the statistical dependence between the latent code and the output image in conditional generative adversarial networks. In addition, by incorporating a U-net generator into our framework, our method only needs to learn a one-sided translation model from the source image domain to the target image domain for both supervised and unsupervised multimodal image-to-image translation. Furthermore, our method also achieves disentanglement between the source domain content and the target domain style for free. We conduct experiments under supervised and unsupervised settings on various benchmark image-to-image translation datasets compared with the state-of-the-art methods, showing the effectiveness and simplicity of our method to achieve multimodal and high-quality results.

Weighted Lasso Estimates for Sparse Logistic Regression: Non-asymptotic Properties with Measurement Error

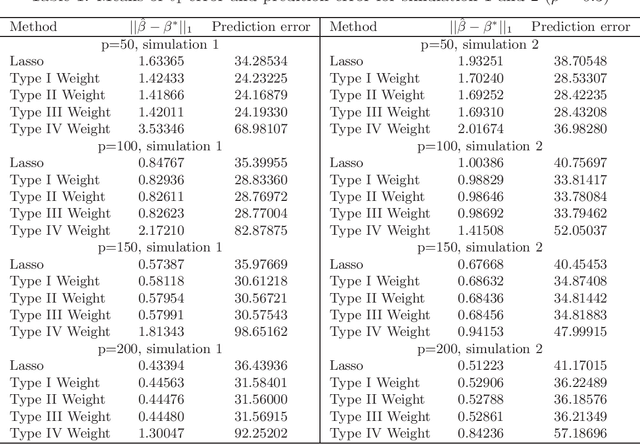
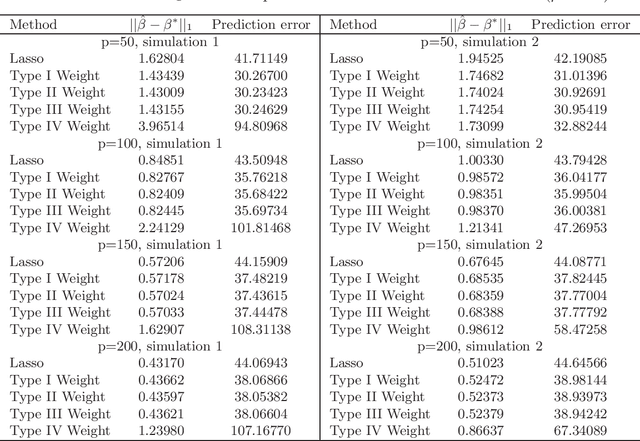
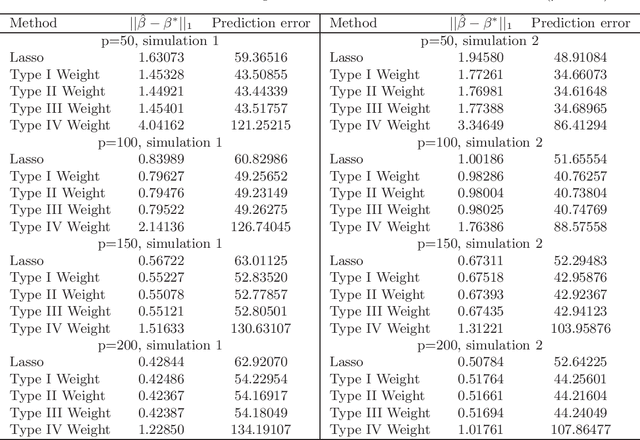
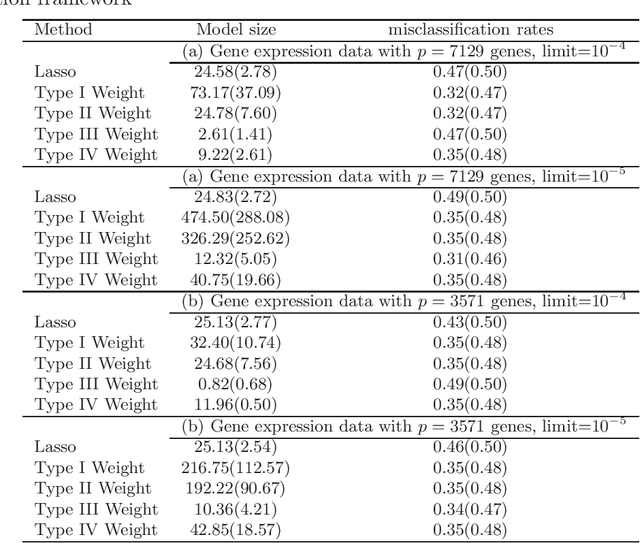
When we are interested in high-dimensional system and focus on classification performance, the $\ell_{1}$-penalized logistic regression is becoming important and popular. However, the Lasso estimates could be problematic when penalties of different coefficients are all the same and not related to the data. We proposed two types of weighted Lasso estimates depending on covariates by the McDiarmid inequality. Given sample size $n$ and dimension of covariates $p$, the finite sample behavior of our proposed methods with a diverging number of predictors is illustrated by non-asymptotic oracle inequalities such as $\ell_{1}$-estimation error and squared prediction error of the unknown parameters. We compare the performance of our methods with former weighted estimates on simulated data, then apply these methods to do real data analysis.

Optimal Distributed Subsampling for Maximum Quasi-Likelihood Estimators with Massive Data

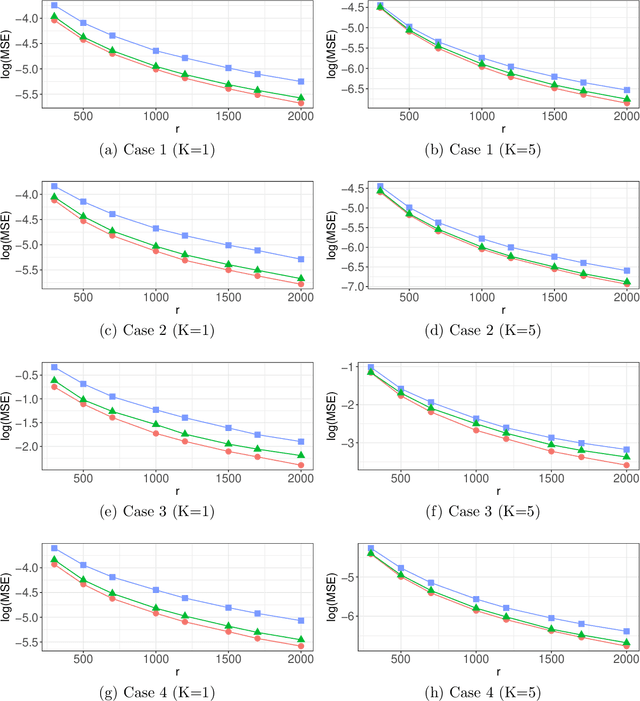
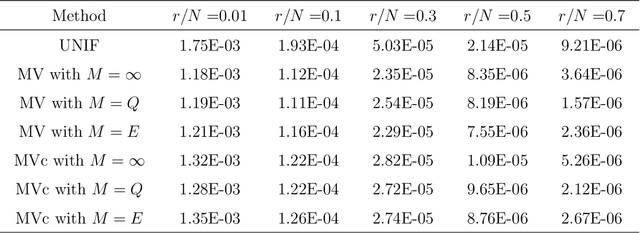
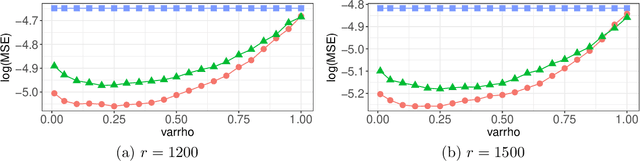
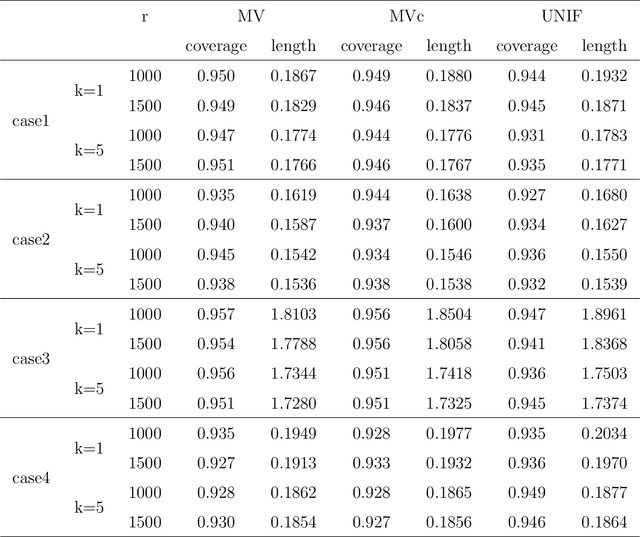
Nonuniform subsampling methods are effective to reduce computational burden and maintain estimation efficiency for massive data. Existing methods mostly focus on subsampling with replacement due to its high computational efficiency. If the data volume is so large that nonuniform subsampling probabilities cannot be calculated all at once, then subsampling with replacement is infeasible to implement. This paper solves this problem using Poisson subsampling. We first derive optimal Poisson subsampling probabilities in the context of quasi-likelihood estimation under the A- and L-optimality criteria. For a practically implementable algorithm with approximated optimal subsampling probabilities, we establish the consistency and asymptotic normality of the resultant estimators. To deal with the situation that the full data are stored in different blocks or at multiple locations, we develop a distributed subsampling framework, in which statistics are computed simultaneously on smaller partitions of the full data. Asymptotic properties of the resultant aggregated estimator are investigated. We illustrate and evaluate the proposed strategies through numerical experiments on simulated and real data sets.

Sparse Density Estimation with Measurement Errors

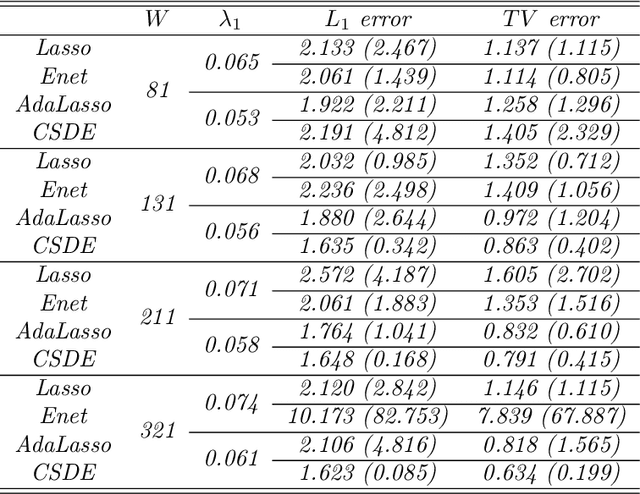
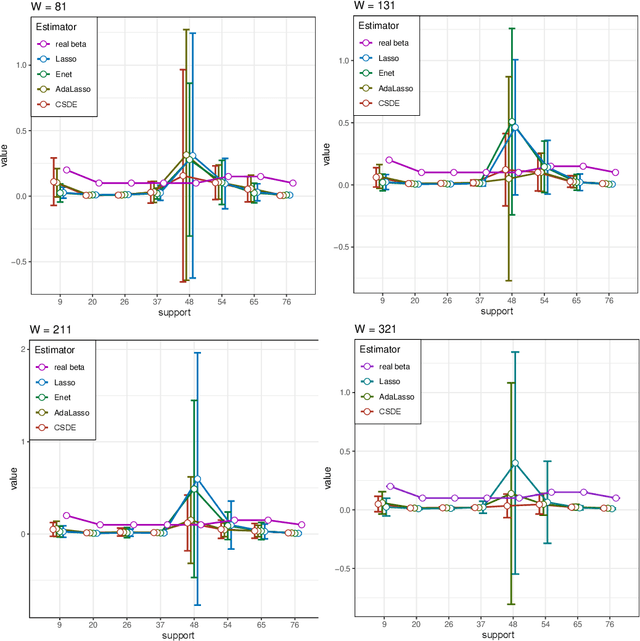
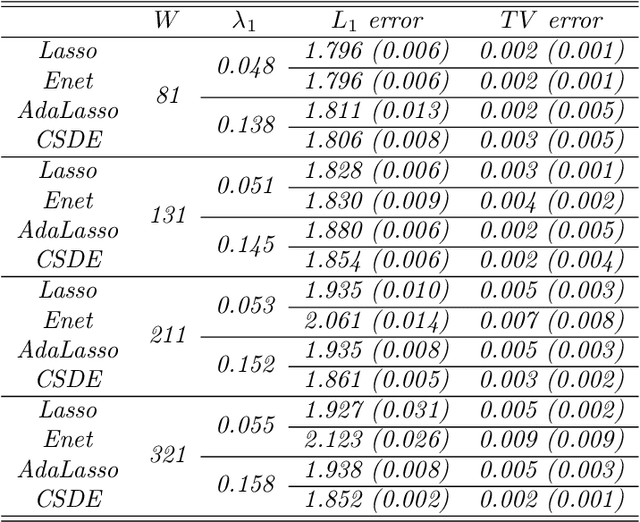
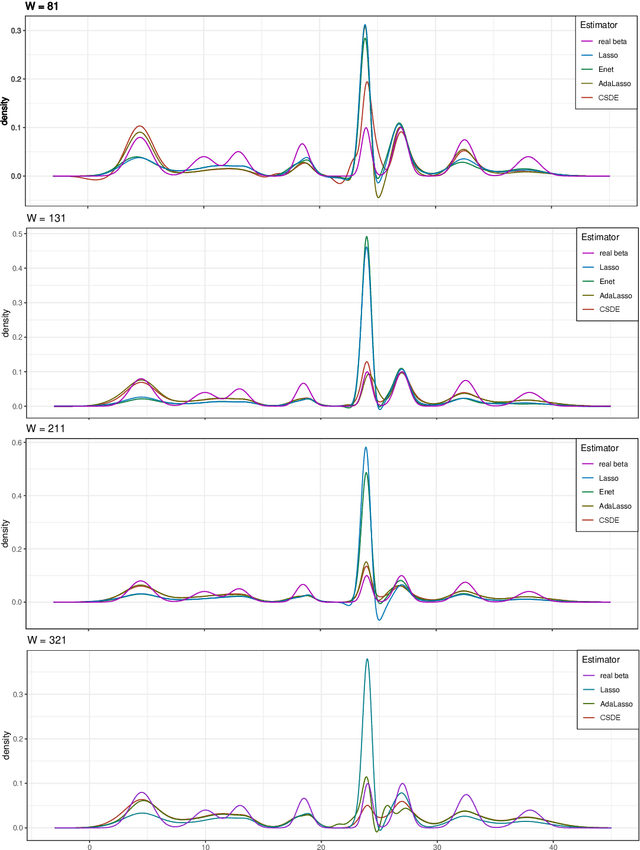
This paper aims to build an estimate of an unknown density of the data with measurement error as a linear combination of functions of a dictionary. Inspired by penalization approach, we propose the weighted Elastic-net penalized minimal $L_2$-distance method for sparse coefficients estimation, where the weights adaptively coming from sharp concentration inequalities. The optimal weighted tuning parameters are obtained by the first-order conditions holding with high-probability. Under local coherence or minimal eigenvalue assumptions, non-asymptotical oracle inequalities are derived. These theoretical results are transposed to obtain the support recovery with high-probability. Then, the issue of calibrating these procedures is studied by some numerical experiments for discrete and continuous distributions, it shows the significant improvement obtained by our procedure when compared with other conventional approaches. Finally, the application is performed for a meteorology data set. It shows that our method has potency and superiority of detecting the shape of multi-mode density compared with other conventional approaches.

Elastic-net regularized High-dimensional Negative Binomial Regression: Consistency and Weak Signals Detection

We study sparse high-dimensional negative binomial regression problem for count data regression by showing non-asymptotic merits of the Elastic-net regularized estimator. With the KKT conditions, we derive two types of non-asymptotic oracle inequalities for the elastic net estimates of negative binomial regression by utilizing Compatibility factor and Stabil Condition, respectively. Based on oracle inequalities we proposed, we firstly show the sign consistency property of the Elastic-net estimators provided that the non-zero components in sparse true vector are large than a proper choice of the weakest signal detection threshold, and the second application is that we give an oracle inequality for bounding the grouping effect with high probability, thirdly, under some assumptions of design matrix, we can recover the true variable set with high probability if the weakest signal detection threshold is large than 3 times the value of turning parameter, at last, we briefly discuss the de-biased Elastic-net estimator.