Nonuniform Negative Sampling and Log Odds Correction with Rare Events Data

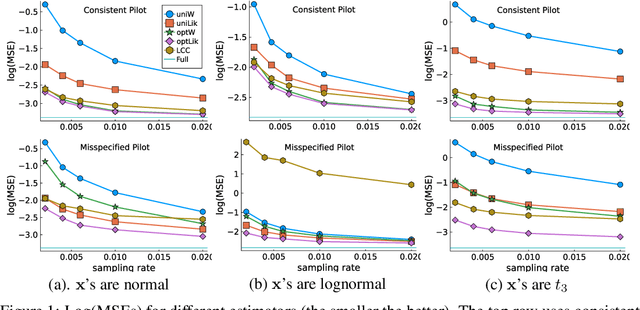
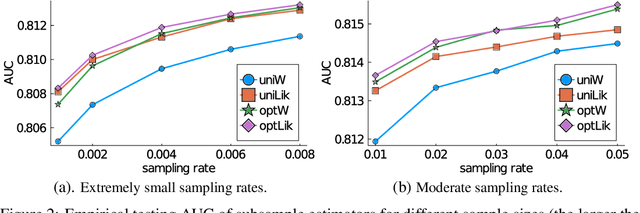
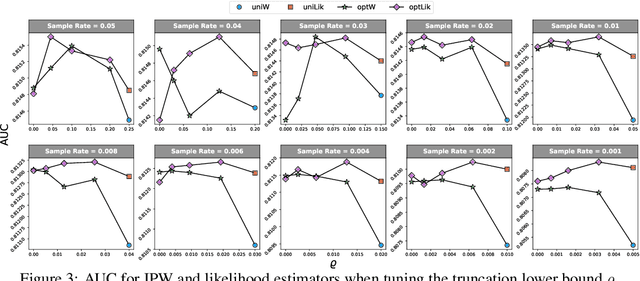
We investigate the issue of parameter estimation with nonuniform negative sampling for imbalanced data. We first prove that, with imbalanced data, the available information about unknown parameters is only tied to the relatively small number of positive instances, which justifies the usage of negative sampling. However, if the negative instances are subsampled to the same level of the positive cases, there is information loss. To maintain more information, we derive the asymptotic distribution of a general inverse probability weighted (IPW) estimator and obtain the optimal sampling probability that minimizes its variance. To further improve the estimation efficiency over the IPW method, we propose a likelihood-based estimator by correcting log odds for the sampled data and prove that the improved estimator has the smallest asymptotic variance among a large class of estimators. It is also more robust to pilot misspecification. We validate our approach on simulated data as well as a real click-through rate dataset with more than 0.3 trillion instances, collected over a period of a month. Both theoretical and empirical results demonstrate the effectiveness of our method.

Maximum sampled conditional likelihood for informative subsampling

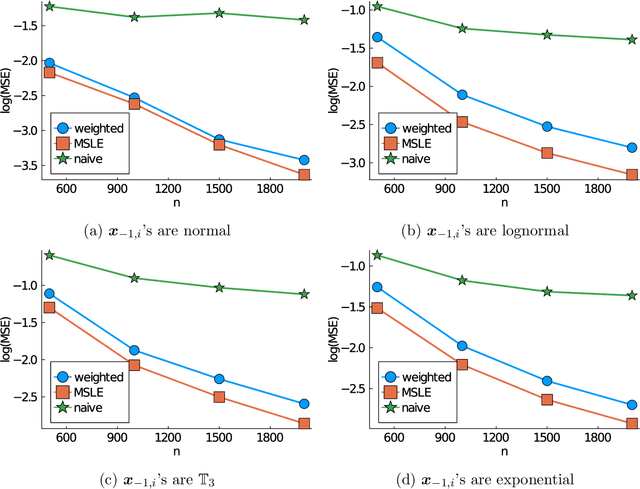
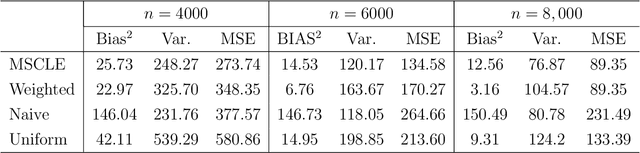
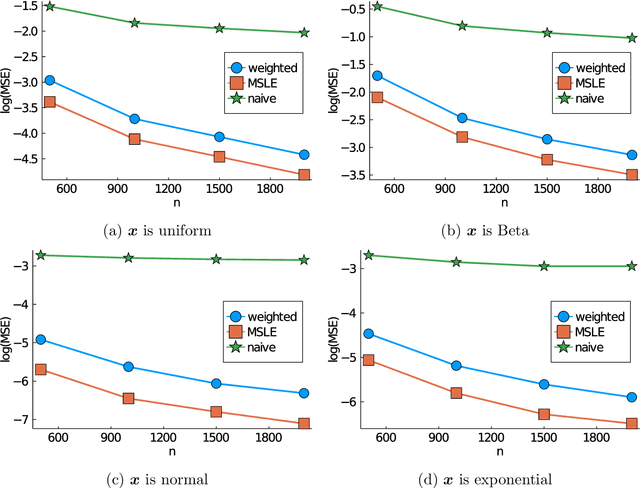
Subsampling is a computationally effective approach to extract information from massive data sets when computing resources are limited. After a subsample is taken from the full data, most available methods use an inverse probability weighted objective function to estimate the model parameters. This type of weighted estimator does not fully utilize information in the selected subsample. In this paper, we propose to use the maximum sampled conditional likelihood estimator (MSCLE) based on the sampled data. We established the asymptotic normality of the MSCLE and prove that its asymptotic variance covariance matrix is the smallest among a class of asymptotically unbiased estimators, including the inverse probability weighted estimator. We further discuss the asymptotic results with the L-optimal subsampling probabilities and illustrate the estimation procedure with generalized linear models. Numerical experiments are provided to evaluate the practical performance of the proposed method.

Reproducible Science with LaTeX

This paper proposes a procedure to execute external source codes from a LaTeX document and include the calculation outputs in the resulting Portable Document Format (pdf) file automatically. It integrates programming tools into the LaTeX writing tool to facilitate the production of reproducible research. In our proposed approach to a LaTeX-based scientific notebook the user can easily invoke any programming language or a command-line program when compiling the LaTeX document, while using their favorite LaTeX editor in the writing process. The required LaTeX setup, a new Python package, and the defined preamble are discussed in detail, and working examples using R, Julia, and MatLab to reproduce existing research are provided to illustrate the proposed procedure. We also demonstrate how to include system setting information in a paper by invoking shell scripts when compiling the document.

Logistic Regression for Massive Data with Rare Events

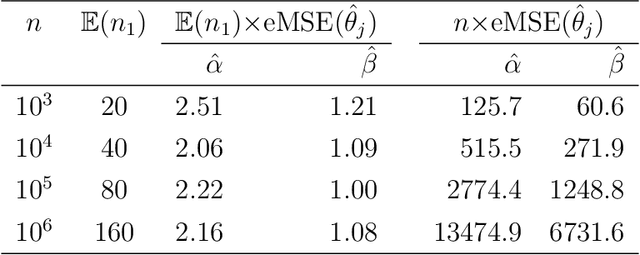
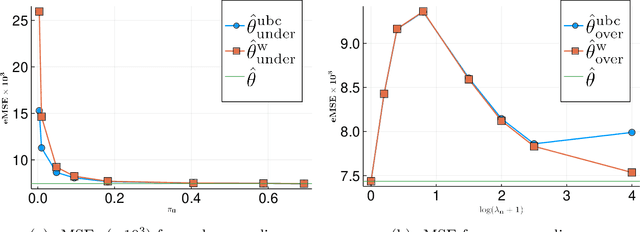
This paper studies binary logistic regression for rare events data, or imbalanced data, where the number of events (observations in one class, often called cases) is significantly smaller than the number of nonevents (observations in the other class, often called controls). We first derive the asymptotic distribution of the maximum likelihood estimator (MLE) of the unknown parameter, which shows that the asymptotic variance convergences to zero in a rate of the inverse of the number of the events instead of the inverse of the full data sample size. This indicates that the available information in rare events data is at the scale of the number of events instead of the full data sample size. Furthermore, we prove that under-sampling a small proportion of the nonevents, the resulting under-sampled estimator may have identical asymptotic distribution to the full data MLE. This demonstrates the advantage of under-sampling nonevents for rare events data, because this procedure may significantly reduce the computation and/or data collection costs. Another common practice in analyzing rare events data is to over-sample (replicate) the events, which has a higher computational cost. We show that this procedure may even result in efficiency loss in terms of parameter estimation.

Optimal Distributed Subsampling for Maximum Quasi-Likelihood Estimators with Massive Data

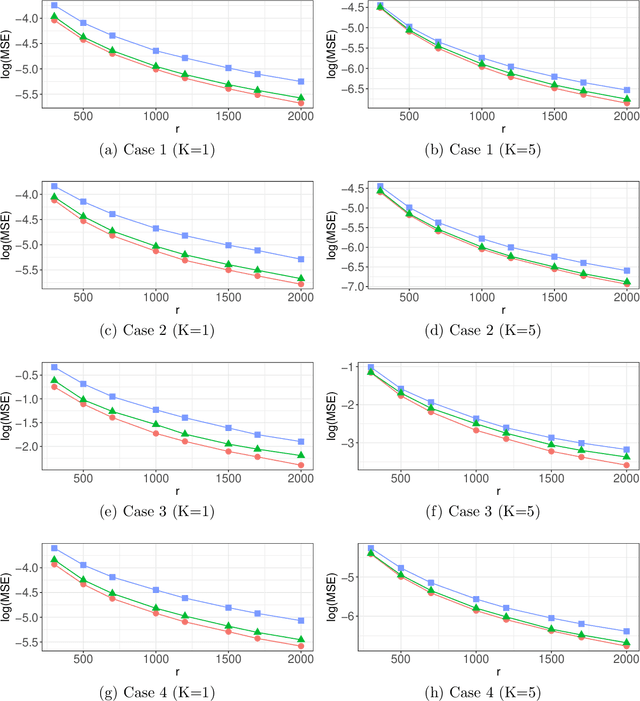
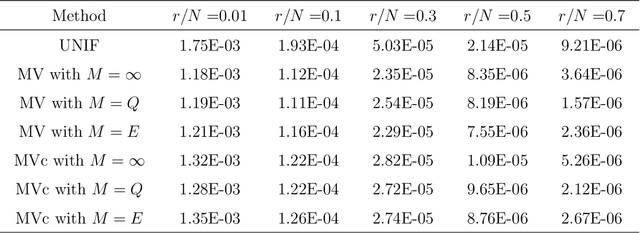
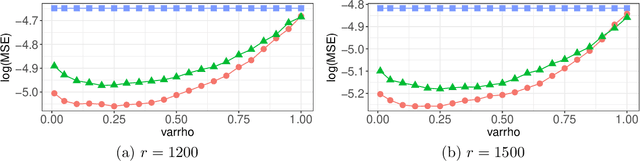
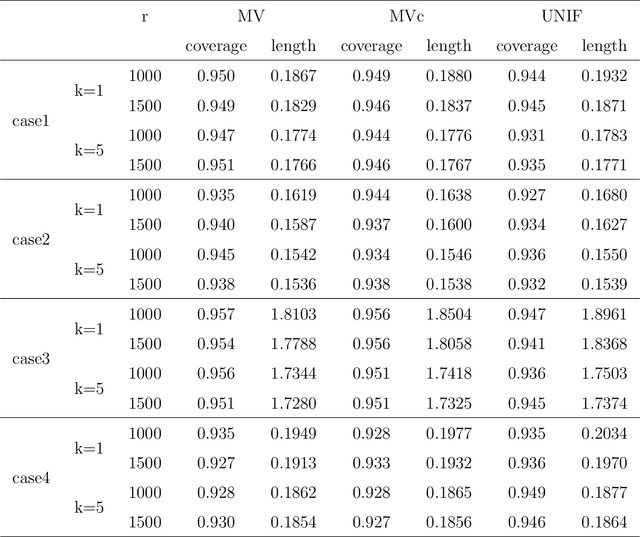
Nonuniform subsampling methods are effective to reduce computational burden and maintain estimation efficiency for massive data. Existing methods mostly focus on subsampling with replacement due to its high computational efficiency. If the data volume is so large that nonuniform subsampling probabilities cannot be calculated all at once, then subsampling with replacement is infeasible to implement. This paper solves this problem using Poisson subsampling. We first derive optimal Poisson subsampling probabilities in the context of quasi-likelihood estimation under the A- and L-optimality criteria. For a practically implementable algorithm with approximated optimal subsampling probabilities, we establish the consistency and asymptotic normality of the resultant estimators. To deal with the situation that the full data are stored in different blocks or at multiple locations, we develop a distributed subsampling framework, in which statistics are computed simultaneously on smaller partitions of the full data. Asymptotic properties of the resultant aggregated estimator are investigated. We illustrate and evaluate the proposed strategies through numerical experiments on simulated and real data sets.

Optimal Subsampling for Large Sample Logistic Regression

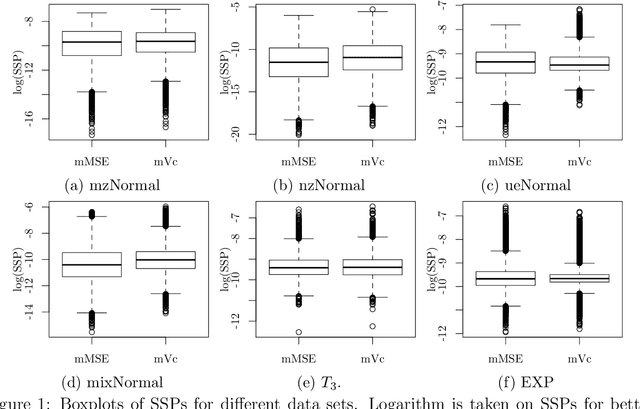
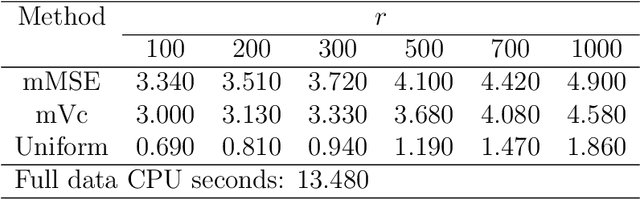
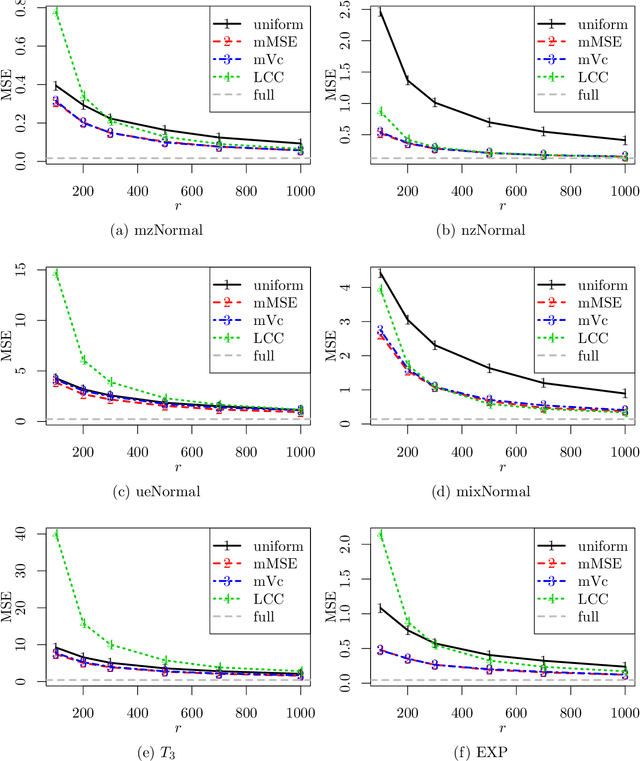
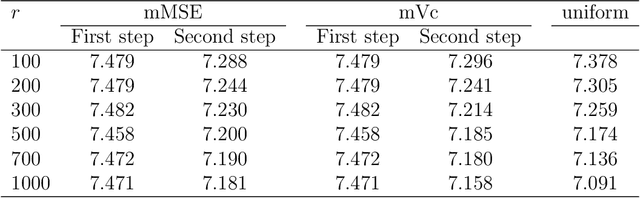
For massive data, the family of subsampling algorithms is popular to downsize the data volume and reduce computational burden. Existing studies focus on approximating the ordinary least squares estimate in linear regression, where statistical leverage scores are often used to define subsampling probabilities. In this paper, we propose fast subsampling algorithms to efficiently approximate the maximum likelihood estimate in logistic regression. We first establish consistency and asymptotic normality of the estimator from a general subsampling algorithm, and then derive optimal subsampling probabilities that minimize the asymptotic mean squared error of the resultant estimator. An alternative minimization criterion is also proposed to further reduce the computational cost. The optimal subsampling probabilities depend on the full data estimate, so we develop a two-step algorithm to approximate the optimal subsampling procedure. This algorithm is computationally efficient and has a significant reduction in computing time compared to the full data approach. Consistency and asymptotic normality of the estimator from a two-step algorithm are also established. Synthetic and real data sets are used to evaluate the practical performance of the proposed method.