Unleashing High-Quality Image Generation in Diffusion Sampling Using Second-Order Levenberg-Marquardt-Langevin

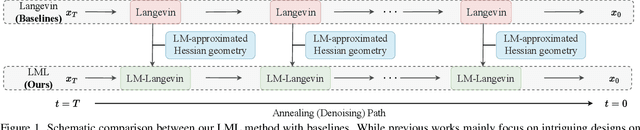
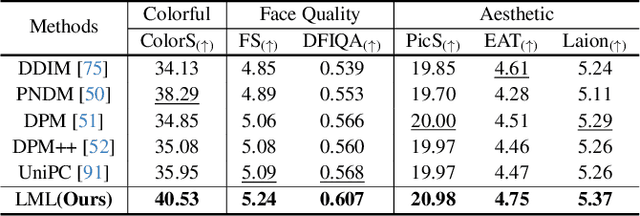
The diffusion models (DMs) have demonstrated the remarkable capability of generating images via learning the noised score function of data distribution. Current DM sampling techniques typically rely on first-order Langevin dynamics at each noise level, with efforts concentrated on refining inter-level denoising strategies. While leveraging additional second-order Hessian geometry to enhance the sampling quality of Langevin is a common practice in Markov chain Monte Carlo (MCMC), the naive attempts to utilize Hessian geometry in high-dimensional DMs lead to quadratic-complexity computational costs, rendering them non-scalable. In this work, we introduce a novel Levenberg-Marquardt-Langevin (LML) method that approximates the diffusion Hessian geometry in a training-free manner, drawing inspiration from the celebrated Levenberg-Marquardt optimization algorithm. Our approach introduces two key innovations: (1) A low-rank approximation of the diffusion Hessian, leveraging the DMs' inherent structure and circumventing explicit quadratic-complexity computations; (2) A damping mechanism to stabilize the approximated Hessian. This LML approximated Hessian geometry enables the diffusion sampling to execute more accurate steps and improve the image generation quality. We further conduct a theoretical analysis to substantiate the approximation error bound of low-rank approximation and the convergence property of the damping mechanism. Extensive experiments across multiple pretrained DMs validate that the LML method significantly improves image generation quality, with negligible computational overhead.

Efficiently Access Diffusion Fisher: Within the Outer Product Span Space

Recent Diffusion models (DMs) advancements have explored incorporating the second-order diffusion Fisher information (DF), defined as the negative Hessian of log density, into various downstream tasks and theoretical analysis. However, current practices typically approximate the diffusion Fisher by applying auto-differentiation to the learned score network. This black-box method, though straightforward, lacks any accuracy guarantee and is time-consuming. In this paper, we show that the diffusion Fisher actually resides within a space spanned by the outer products of score and initial data. Based on the outer-product structure, we develop two efficient approximation algorithms to access the trace and matrix-vector multiplication of DF, respectively. These algorithms bypass the auto-differentiation operations with time-efficient vector-product calculations. Furthermore, we establish the approximation error bounds for the proposed algorithms. Experiments in likelihood evaluation and adjoint optimization demonstrate the superior accuracy and reduced computational cost of our proposed algorithms. Additionally, based on the novel outer-product formulation of DF, we design the first numerical verification experiment for the optimal transport property of the general PF-ODE deduced map.

BELM: Bidirectional Explicit Linear Multi-step Sampler for Exact Inversion in Diffusion Models

The inversion of diffusion model sampling, which aims to find the corresponding initial noise of a sample, plays a critical role in various tasks. Recently, several heuristic exact inversion samplers have been proposed to address the inexact inversion issue in a training-free manner. However, the theoretical properties of these heuristic samplers remain unknown and they often exhibit mediocre sampling quality. In this paper, we introduce a generic formulation, \emph{Bidirectional Explicit Linear Multi-step} (BELM) samplers, of the exact inversion samplers, which includes all previously proposed heuristic exact inversion samplers as special cases. The BELM formulation is derived from the variable-stepsize-variable-formula linear multi-step method via integrating a bidirectional explicit constraint. We highlight this bidirectional explicit constraint is the key of mathematically exact inversion. We systematically investigate the Local Truncation Error (LTE) within the BELM framework and show that the existing heuristic designs of exact inversion samplers yield sub-optimal LTE. Consequently, we propose the Optimal BELM (O-BELM) sampler through the LTE minimization approach. We conduct additional analysis to substantiate the theoretical stability and global convergence property of the proposed optimal sampler. Comprehensive experiments demonstrate our O-BELM sampler establishes the exact inversion property while achieving high-quality sampling. Additional experiments in image editing and image interpolation highlight the extensive potential of applying O-BELM in varying applications.

Tackling the Singularities at the Endpoints of Time Intervals in Diffusion Models

Most diffusion models assume that the reverse process adheres to a Gaussian distribution. However, this approximation has not been rigorously validated, especially at singularities, where t=0 and t=1. Improperly dealing with such singularities leads to an average brightness issue in applications, and limits the generation of images with extreme brightness or darkness. We primarily focus on tackling singularities from both theoretical and practical perspectives. Initially, we establish the error bounds for the reverse process approximation, and showcase its Gaussian characteristics at singularity time steps. Based on this theoretical insight, we confirm the singularity at t=1 is conditionally removable while it at t=0 is an inherent property. Upon these significant conclusions, we propose a novel plug-and-play method SingDiffusion to address the initial singular time step sampling, which not only effectively resolves the average brightness issue for a wide range of diffusion models without extra training efforts, but also enhances their generation capability in achieving notable lower FID scores.

Formulating Discrete Probability Flow Through Optimal Transport

Continuous diffusion models are commonly acknowledged to display a deterministic probability flow, whereas discrete diffusion models do not. In this paper, we aim to establish the fundamental theory for the probability flow of discrete diffusion models. Specifically, we first prove that the continuous probability flow is the Monge optimal transport map under certain conditions, and also present an equivalent evidence for discrete cases. In view of these findings, we are then able to define the discrete probability flow in line with the principles of optimal transport. Finally, drawing upon our newly established definitions, we propose a novel sampling method that surpasses previous discrete diffusion models in its ability to generate more certain outcomes. Extensive experiments on the synthetic toy dataset and the CIFAR-10 dataset have validated the effectiveness of our proposed discrete probability flow. Code is released at: https://github.com/PangzeCheung/Discrete-Probability-Flow.