Harnessing Adaptive Topology Representations for Zero-Shot Graph Question Answering

Large Multimodal Models (LMMs) have shown generalized zero-shot capabilities in diverse domain question-answering (QA) tasks, including graph QA that involves complex graph topologies. However, most current approaches use only a single type of graph representation, namely Topology Representation Form (TRF), such as prompt-unified text descriptions or style-fixed visual styles. Those "one-size-fits-all" approaches fail to consider the specific preferences of different models or tasks, often leading to incorrect or overly long responses. To address this, we first analyze the characteristics and weaknesses of existing TRFs, and then design a set of TRFs, denoted by $F_{ZS}$, tailored to zero-shot graph QA. We then introduce a new metric, Graph Response Efficiency (GRE), which measures the balance between the performance and the brevity in graph QA. Built on these, we develop the DynamicTRF framework, which aims to improve both the accuracy and conciseness of graph QA. To be specific, DynamicTRF first creates a TRF Preference (TRFP) dataset that ranks TRFs based on their GRE scores, to probe the question-specific TRF preferences. Then it trains a TRF router on the TRFP dataset, to adaptively assign the best TRF from $F_{ZS}$ for each question during the inference. Extensive experiments across 7 in-domain algorithmic graph QA tasks and 2 out-of-domain downstream tasks show that DynamicTRF significantly enhances the zero-shot graph QA of LMMs in terms of accuracy

Elastic Graph Neural Networks

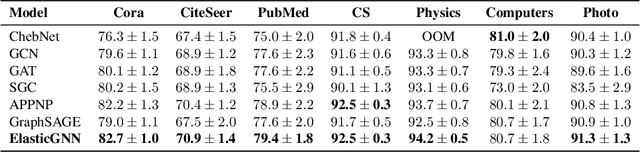
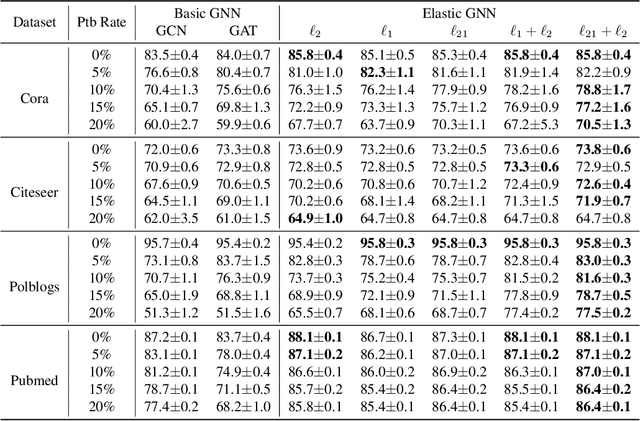
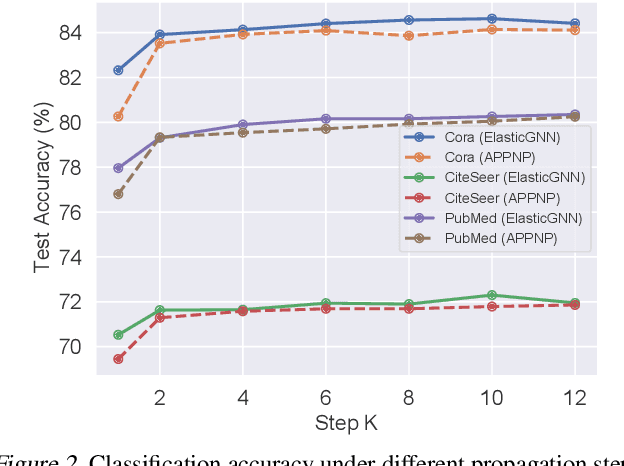
While many existing graph neural networks (GNNs) have been proven to perform $\ell_2$-based graph smoothing that enforces smoothness globally, in this work we aim to further enhance the local smoothness adaptivity of GNNs via $\ell_1$-based graph smoothing. As a result, we introduce a family of GNNs (Elastic GNNs) based on $\ell_1$ and $\ell_2$-based graph smoothing. In particular, we propose a novel and general message passing scheme into GNNs. This message passing algorithm is not only friendly to back-propagation training but also achieves the desired smoothing properties with a theoretical convergence guarantee. Experiments on semi-supervised learning tasks demonstrate that the proposed Elastic GNNs obtain better adaptivity on benchmark datasets and are significantly robust to graph adversarial attacks. The implementation of Elastic GNNs is available at \url{https://github.com/lxiaorui/ElasticGNN}.