CMPhysBench: A Benchmark for Evaluating Large Language Models in Condensed Matter Physics

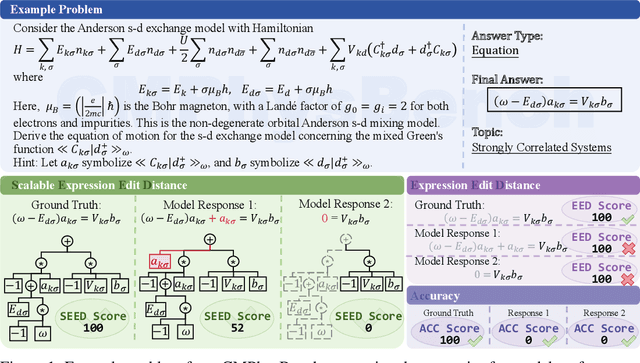
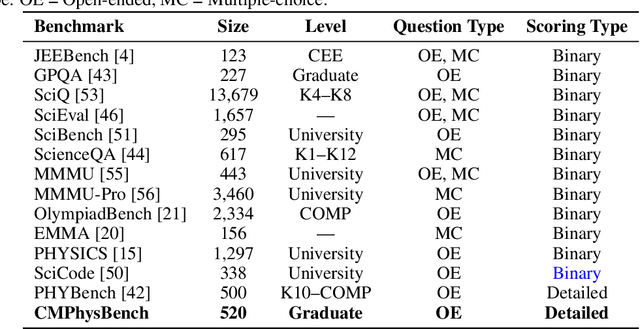
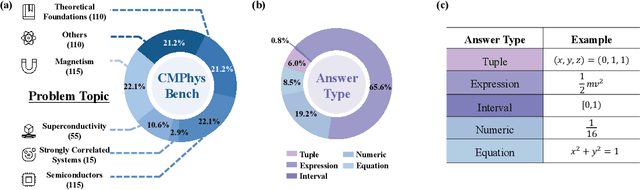
We introduce CMPhysBench, designed to assess the proficiency of Large Language Models (LLMs) in Condensed Matter Physics, as a novel Benchmark. CMPhysBench is composed of more than 520 graduate-level meticulously curated questions covering both representative subfields and foundational theoretical frameworks of condensed matter physics, such as magnetism, superconductivity, strongly correlated systems, etc. To ensure a deep understanding of the problem-solving process,we focus exclusively on calculation problems, requiring LLMs to independently generate comprehensive solutions. Meanwhile, leveraging tree-based representations of expressions, we introduce the Scalable Expression Edit Distance (SEED) score, which provides fine-grained (non-binary) partial credit and yields a more accurate assessment of similarity between prediction and ground-truth. Our results show that even the best models, Grok-4, reach only 36 average SEED score and 28% accuracy on CMPhysBench, underscoring a significant capability gap, especially for this practical and frontier domain relative to traditional physics. The code anddataset are publicly available at https://github.com/CMPhysBench/CMPhysBench.

Training-set-free two-stage deep learning for spectroscopic data de-noising

De-noising is a prominent step in the spectra post-processing procedure. Previous machine learning-based methods are fast but mostly based on supervised learning and require a training set that may be typically expensive in real experimental measurements. Unsupervised learning-based algorithms are slow and require many iterations to achieve convergence. Here, we bridge this gap by proposing a training-set-free two-stage deep learning method. We show that the fuzzy fixed input in previous methods can be improved by introducing an adaptive prior. Combined with more advanced optimization techniques, our approach can achieve five times acceleration compared to previous work. Theoretically, we study the landscape of a corresponding non-convex linear problem, and our results indicates that this problem has benign geometry for first-order algorithms to converge.