Quantifying Epistemic Uncertainty in Deep Learning

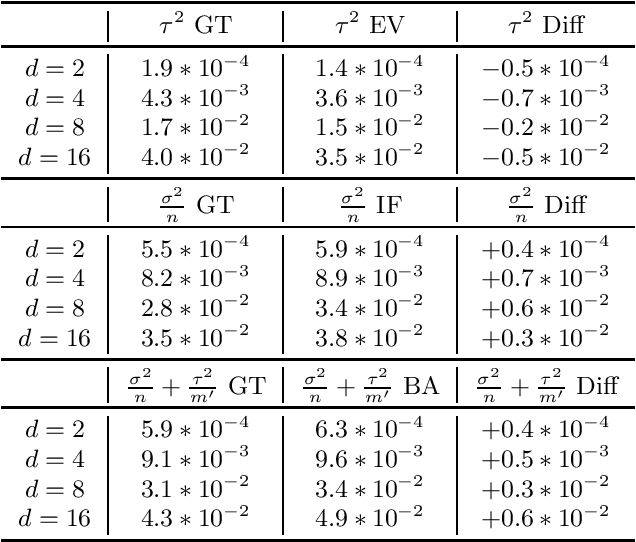
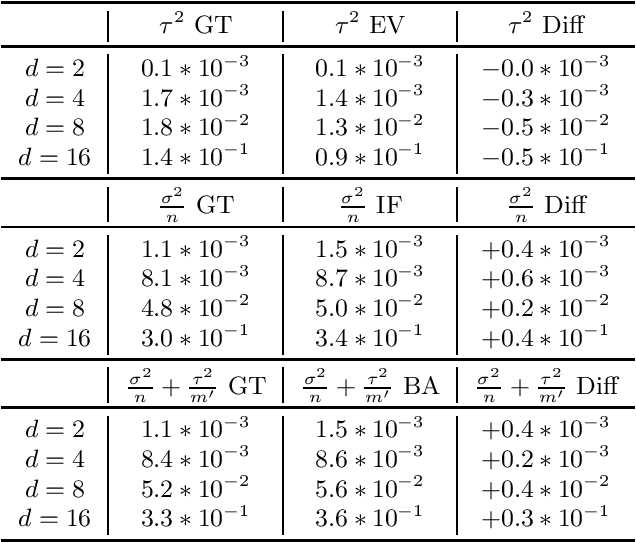
Uncertainty quantification is at the core of the reliability and robustness of machine learning. It is well-known that uncertainty consists of two different types, often referred to as aleatoric and epistemic uncertainties. In this paper, we provide a systematic study on the epistemic uncertainty in deep supervised learning. We rigorously distinguish different sources of epistemic uncertainty, including in particular procedural variability (from the training procedure) and data variability (from the training data). We use our framework to explain how deep ensemble enhances prediction by reducing procedural variability. We also propose two approaches to estimate epistemic uncertainty for a well-trained neural network in practice. One uses influence function derived from the theory of neural tangent kernel that bypasses the convexity assumption violated by modern neural networks. Another uses batching that bypasses the time-consuming Gram matrix inversion in the influence function calculation, while expending minimal re-training effort. We discuss how both approaches overcome some difficulties in applying classical statistical methods to the inference on deep learning.

Complexity-Free Generalization via Distributionally Robust Optimization

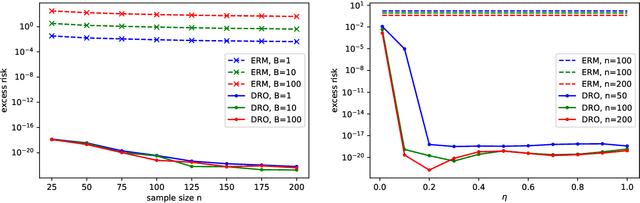
Established approaches to obtain generalization bounds in data-driven optimization and machine learning mostly build on solutions from empirical risk minimization (ERM), which depend crucially on the functional complexity of the hypothesis class. In this paper, we present an alternate route to obtain these bounds on the solution from distributionally robust optimization (DRO), a recent data-driven optimization framework based on worst-case analysis and the notion of ambiguity set to capture statistical uncertainty. In contrast to the hypothesis class complexity in ERM, our DRO bounds depend on the ambiguity set geometry and its compatibility with the true loss function. Notably, when using maximum mean discrepancy as a DRO distance metric, our analysis implies, to the best of our knowledge, the first generalization bound in the literature that depends solely on the true loss function, entirely free of any complexity measures or bounds on the hypothesis class.

Accelerated Policy Evaluation: Learning Adversarial Environments with Adaptive Importance Sampling

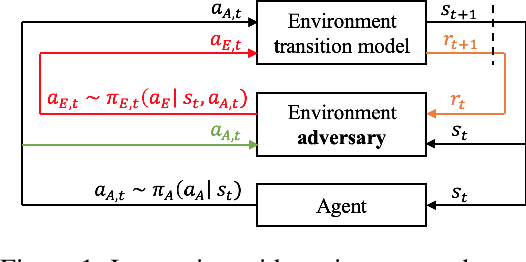
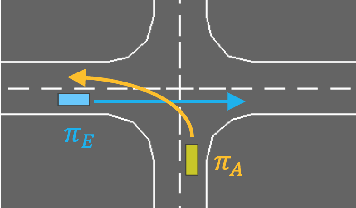
The evaluation of rare but high-stakes events remains one of the main difficulties in obtaining reliable policies from intelligent agents, especially in large or continuous state/action spaces where limited scalability enforces the use of a prohibitively large number of testing iterations. On the other hand, a biased or inaccurate policy evaluation in a safety-critical system could potentially cause unexpected catastrophic failures during deployment. In this paper, we propose the Accelerated Policy Evaluation (APE) method, which simultaneously uncovers rare events and estimates the rare event probability in Markov decision processes. The APE method treats the environment nature as an adversarial agent and learns towards, through adaptive importance sampling, the zero-variance sampling distribution for the policy evaluation. Moreover, APE is scalable to large discrete or continuous spaces by incorporating function approximators. We investigate the convergence properties of proposed algorithms under suitable regularity conditions. Our empirical studies show that APE estimates rare event probability with a smaller variance while only using orders of magnitude fewer samples compared to baseline methods in both multi-agent and single-agent environments.

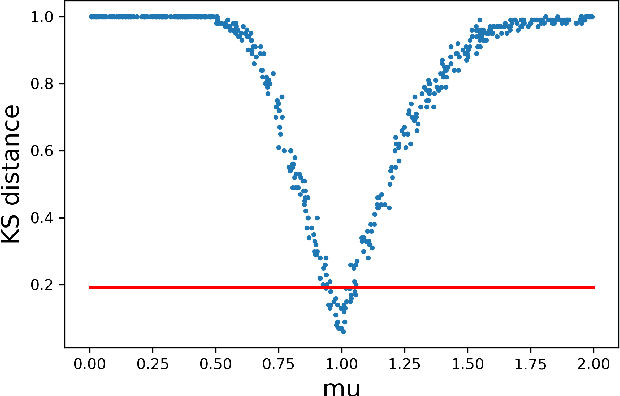
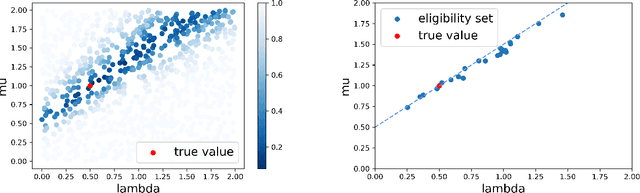
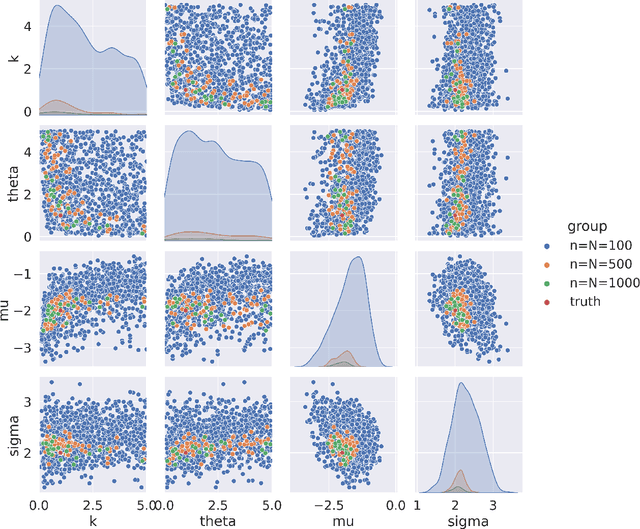
Calibrating Over-Parametrized Simulation Models: A Framework via Eligibility Set

Stochastic simulation aims to compute output performance for complex models that lack analytical tractability. To ensure accurate prediction, the model needs to be calibrated and validated against real data. Conventional methods approach these tasks by assessing the model-data match via simple hypothesis tests or distance minimization in an ad hoc fashion, but they can encounter challenges arising from non-identifiability and high dimensionality. In this paper, we investigate a framework to develop calibration schemes that satisfy rigorous frequentist statistical guarantees, via a basic notion that we call eligibility set designed to bypass non-identifiability via a set-based estimation. We investigate a feature extraction-then-aggregation approach to construct these sets that target at multivariate outputs. We demonstrate our methodology on several numerical examples, including an application to calibration of a limit order book market simulator (ABIDES).

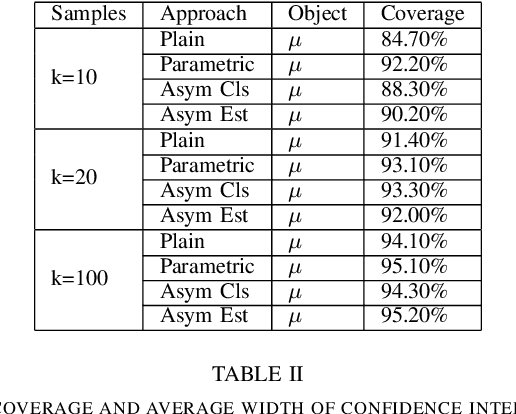
Learning Prediction Intervals for Regression: Generalization and Calibration

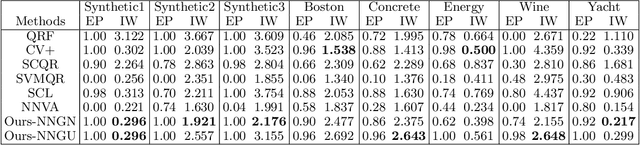
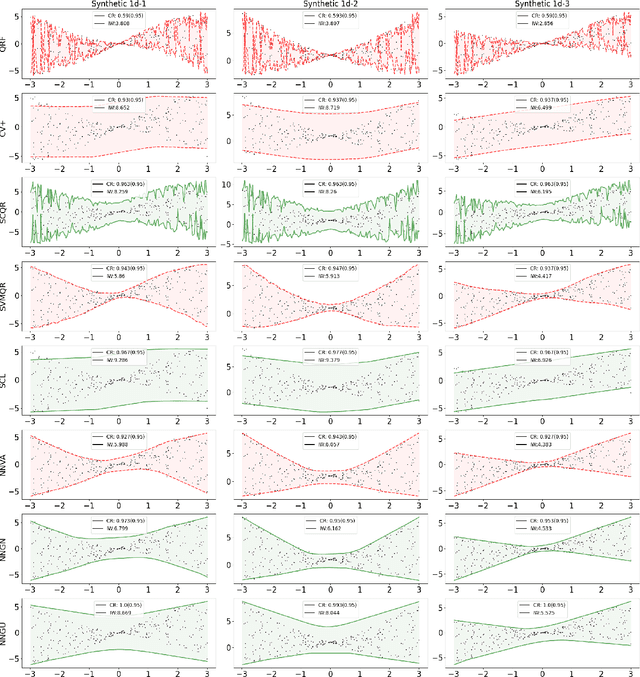
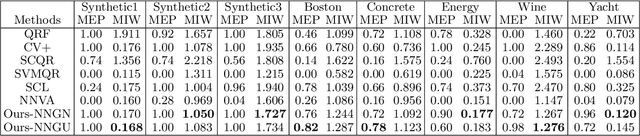
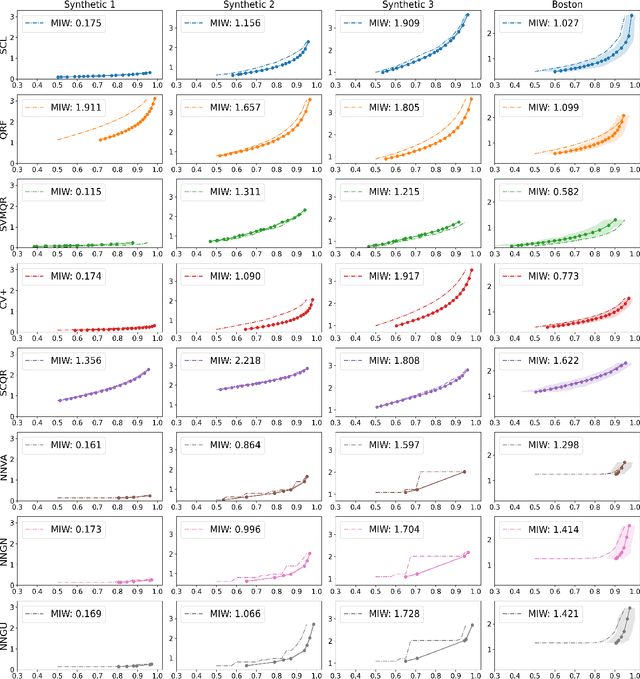
We study the generation of prediction intervals in regression for uncertainty quantification. This task can be formalized as an empirical constrained optimization problem that minimizes the average interval width while maintaining the coverage accuracy across data. We strengthen the existing literature by studying two aspects of this empirical optimization. First is a general learning theory to characterize the optimality-feasibility tradeoff that encompasses Lipschitz continuity and VC-subgraph classes, which are exemplified in regression trees and neural networks. Second is a calibration machinery and the corresponding statistical theory to optimally select the regularization parameter that manages this tradeoff, which bypasses the overfitting issues in previous approaches in coverage attainment. We empirically demonstrate the strengths of our interval generation and calibration algorithms in terms of testing performances compared to existing benchmarks.

Rare-Event Simulation for Neural Network and Random Forest Predictors

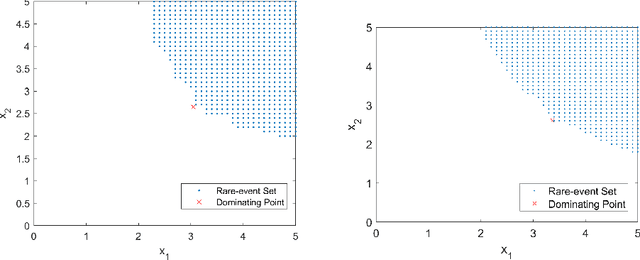
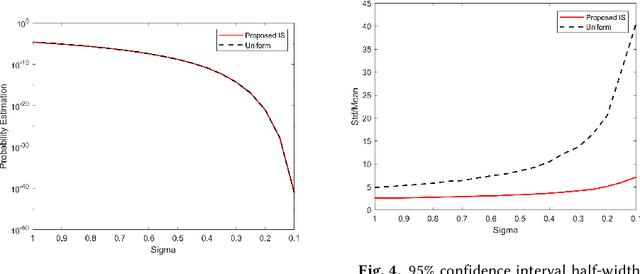
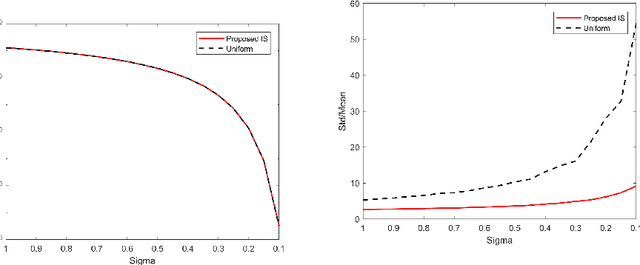
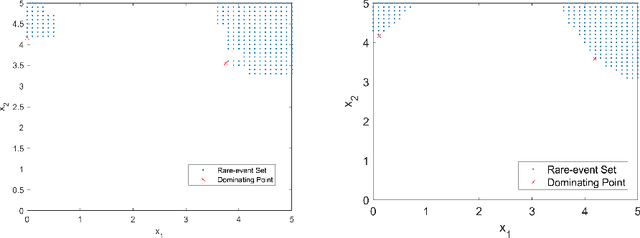
We study rare-event simulation for a class of problems where the target hitting sets of interest are defined via modern machine learning tools such as neural networks and random forests. This problem is motivated from fast emerging studies on the safety evaluation of intelligent systems, robustness quantification of learning models, and other potential applications to large-scale simulation in which machine learning tools can be used to approximate complex rare-event set boundaries. We investigate an importance sampling scheme that integrates the dominating point machinery in large deviations and sequential mixed integer programming to locate the underlying dominating points. Our approach works for a range of neural network architectures including fully connected layers, rectified linear units, normalization, pooling and convolutional layers, and random forests built from standard decision trees. We provide efficiency guarantees and numerical demonstration of our approach using a classification model in the UCI Machine Learning Repository.

Deep Probabilistic Accelerated Evaluation: A Certifiable Rare-Event Simulation Methodology for Black-Box Autonomy

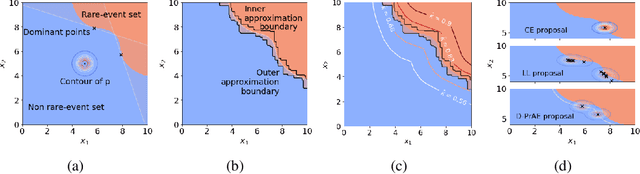
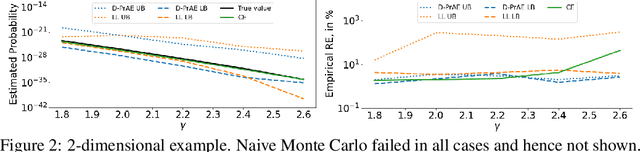
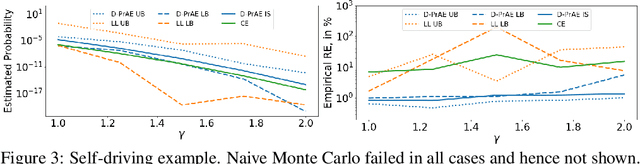
Evaluating the reliability of intelligent physical systems against rare catastrophic events poses a huge testing burden for real-world applications. Simulation provides a useful, if not unique, platform to evaluate the extremal risks of these AI-enabled systems before their deployments. Importance Sampling (IS), while proven to be powerful for rare-event simulation, faces challenges in handling these systems due to their black-box nature that fundamentally undermines its efficiency guarantee. To overcome this challenge, we propose a framework called Deep Probabilistic Accelerated Evaluation (D-PrAE) to design IS, which leverages rare-event-set learning and a new notion of efficiency certificate. D-PrAE combines the dominating point method with deep neural network classifiers to achieve superior estimation efficiency. We present theoretical guarantees and demonstrate the empirical effectiveness of D-PrAE via examples on the safety-testing of self-driving algorithms that are beyond the reach of classical variance reduction techniques.

Efficient Inference and Exploration for Reinforcement Learning

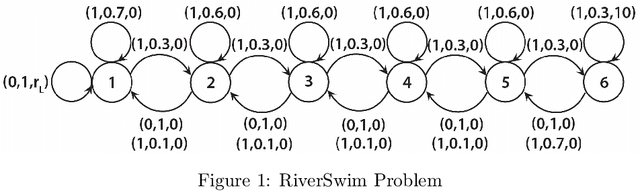
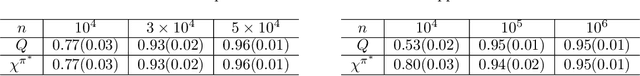
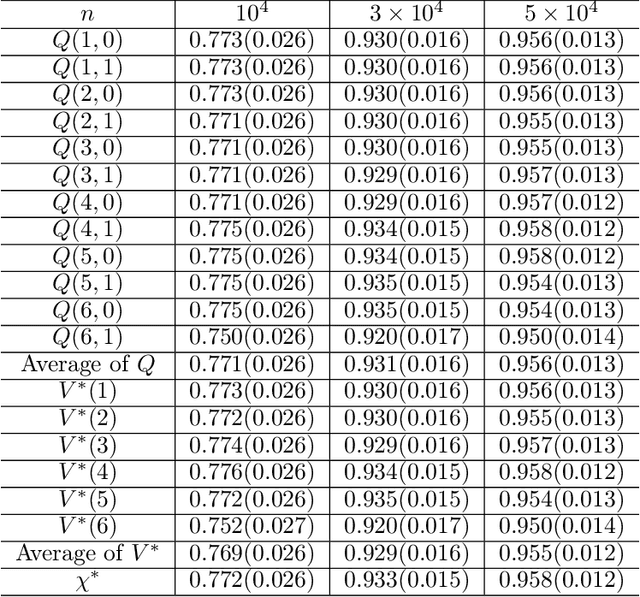
Despite an ever growing literature on reinforcement learning algorithms and applications, much less is known about their statistical inference. In this paper, we investigate the large sample behaviors of the Q-value estimates with closed-form characterizations of the asymptotic variances. This allows us to efficiently construct confidence regions for Q-value and optimal value functions, and to develop policies to minimize their estimation errors. This also leads to a policy exploration strategy that relies on estimating the relative discrepancies among the Q estimates. Numerical experiments show superior performances of our exploration strategy than other benchmark approaches.

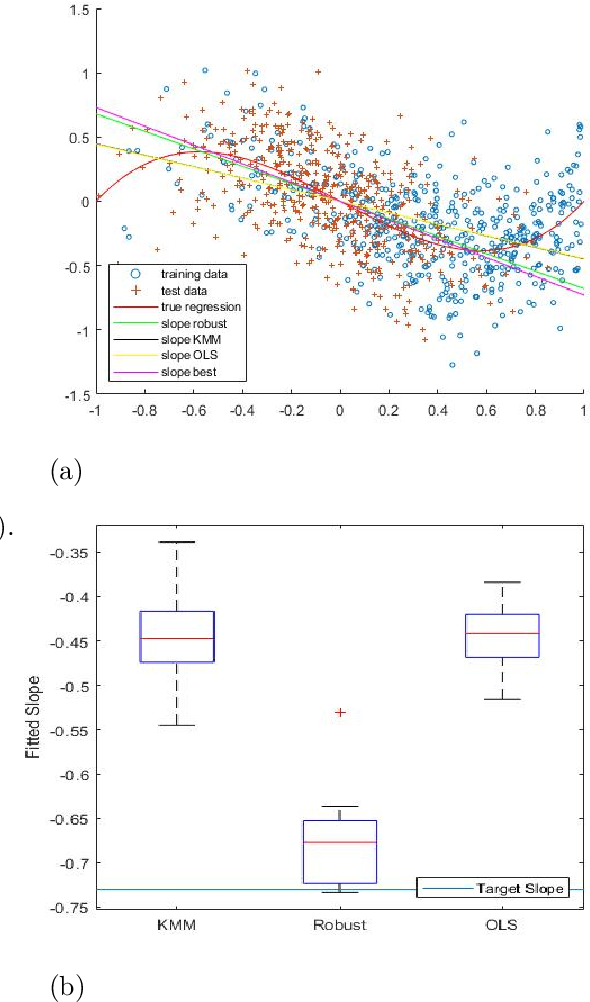
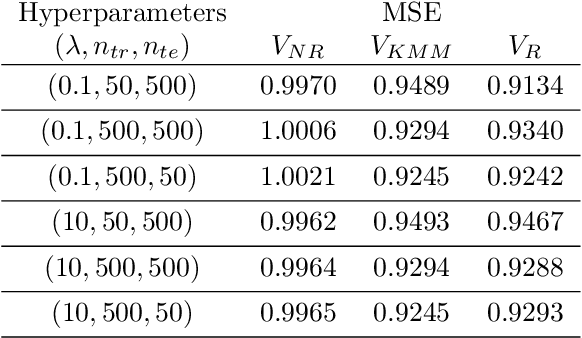
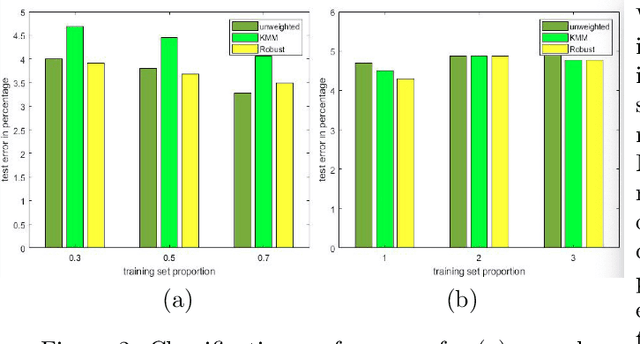
Robust Importance Weighting for Covariate Shift

In many learning problems, the training and testing data follow different distributions and a particularly common situation is the \textit{covariate shift}. To correct for sampling biases, most approaches, including the popular kernel mean matching (KMM), focus on estimating the importance weights between the two distributions. Reweighting-based methods, however, are exposed to high variance when the distributional discrepancy is large and the weights are poorly estimated. On the other hand, the alternate approach of using nonparametric regression (NR) incurs high bias when the training size is limited. In this paper, we propose and analyze a new estimator that systematically integrates the residuals of NR with KMM reweighting, based on a control-variate perspective. The proposed estimator can be shown to either strictly outperform or match the best-known existing rates for both KMM and NR, and thus is a robust combination of both estimators. The experiments shows the estimator works well in practice.

Assessing Modeling Variability in Autonomous Vehicle Accelerated Evaluation

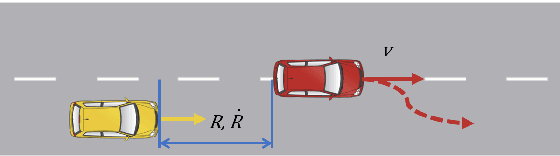
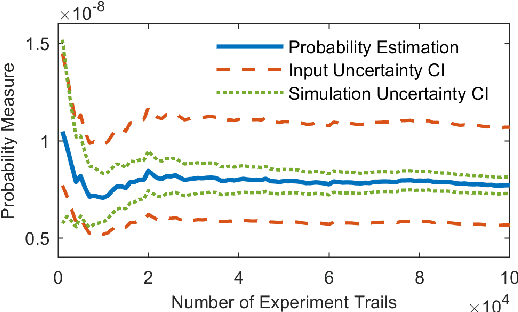
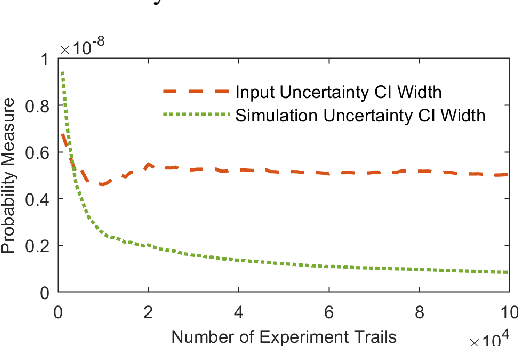
Safety evaluation of autonomous vehicles is extensively studied recently, one line of studies considers Monte Carlo based evaluation. The Monte Carlo based evaluation usually estimates the probability of safety-critical events as a safety measurement based on Monte Carlo samples. These Monte Carlo samples are generated from a stochastic model that is constructed based on real-world data. In this paper, we propose an approach to assess the potential estimation error in the evaluation procedure caused by data variability. The proposed method merges the classical bootstrap method for estimating input uncertainty with a likelihood ratio based scheme to reuse experiment results. The proposed approach is highly economical and efficient in terms of implementation costs in assessing input uncertainty for autonomous vehicle evaluation.