A New Framework for Variance-Reduced Hamiltonian Monte Carlo

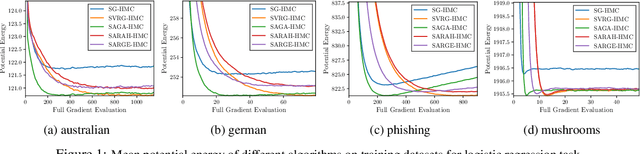
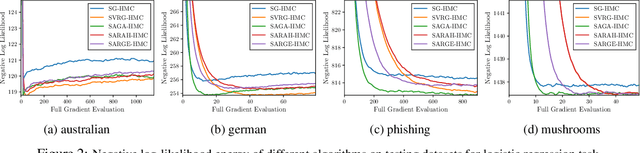
We propose a new framework of variance-reduced Hamiltonian Monte Carlo (HMC) methods for sampling from an $L$-smooth and $m$-strongly log-concave distribution, based on a unified formulation of biased and unbiased variance reduction methods. We study the convergence properties for HMC with gradient estimators which satisfy the Mean-Squared-Error-Bias (MSEB) property. We show that the unbiased gradient estimators, including SAGA and SVRG, based HMC methods achieve highest gradient efficiency with small batch size under high precision regime, and require $\tilde{O}(N + \kappa^2 d^{\frac{1}{2}} \varepsilon^{-1} + N^{\frac{2}{3}} \kappa^{\frac{4}{3}} d^{\frac{1}{3}} \varepsilon^{-\frac{2}{3}} )$ gradient complexity to achieve $\epsilon$-accuracy in 2-Wasserstein distance. Moreover, our HMC methods with biased gradient estimators, such as SARAH and SARGE, require $\tilde{O}(N+\sqrt{N} \kappa^2 d^{\frac{1}{2}} \varepsilon^{-1})$ gradient complexity, which has the same dependency on condition number $\kappa$ and dimension $d$ as full gradient method, but improves the dependency of sample size $N$ for a factor of $N^\frac{1}{2}$. Experimental results on both synthetic and real-world benchmark data show that our new framework significantly outperforms the full gradient and stochastic gradient HMC approaches. The earliest version of this paper was submitted to ICML 2020 with three weak accept but was not finally accepted.

Double Momentum SGD for Federated Learning

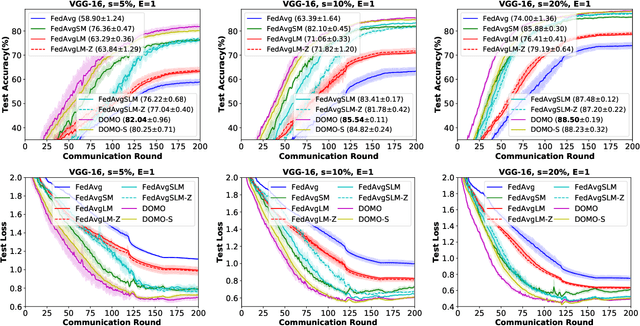
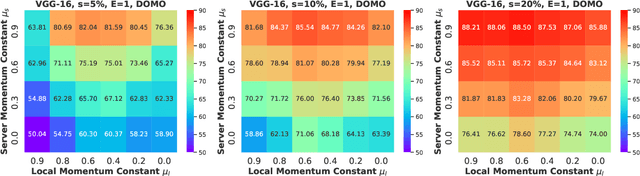
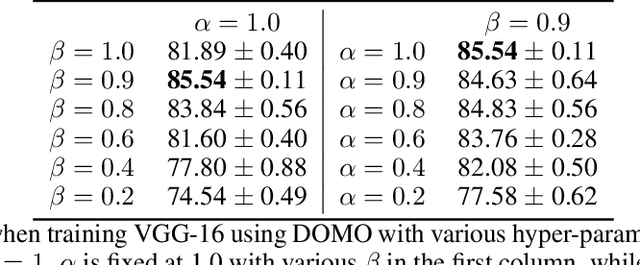
Communication efficiency is crucial in federated learning. Conducting many local training steps in clients to reduce the communication frequency between clients and the server is a common method to address this issue. However, the client drift problem arises as the non-i.i.d. data distributions in different clients can severely deteriorate the performance of federated learning. In this work, we propose a new SGD variant named as DOMO to improve the model performance in federated learning, where double momentum buffers are maintained. One momentum buffer tracks the server update direction, while the other tracks the local update direction. We introduce a novel server momentum fusion technique to coordinate the server and local momentum SGD. We also provide the first theoretical analysis involving both the server and local momentum SGD. Extensive experimental results show a better model performance of DOMO than FedAvg and existing momentum SGD variants in federated learning tasks.

H2NF-Net for Brain Tumor Segmentation using Multimodal MR Imaging: 2nd Place Solution to BraTS Challenge 2020 Segmentation Task

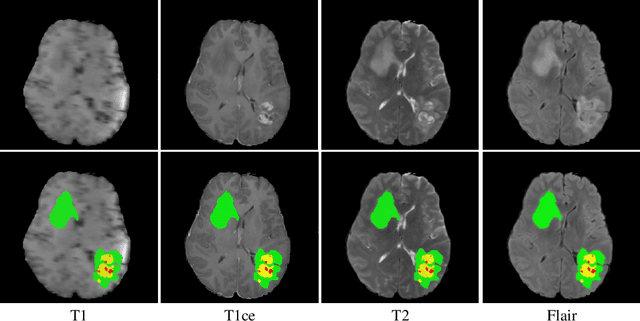
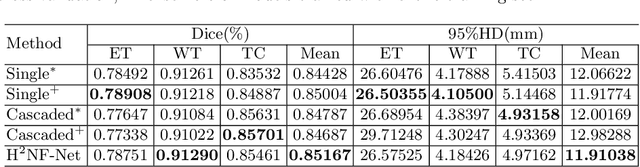
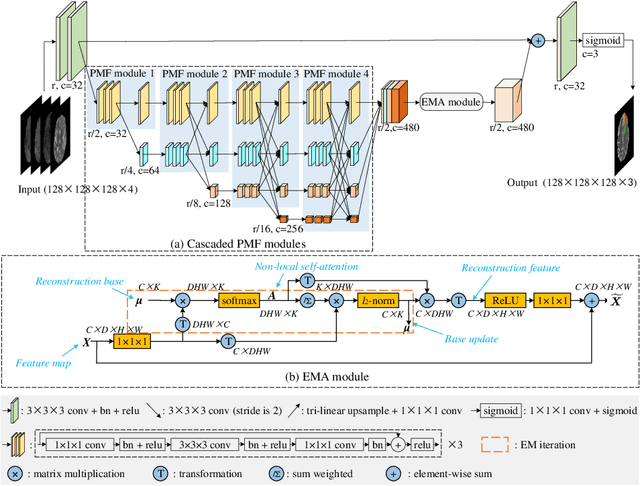
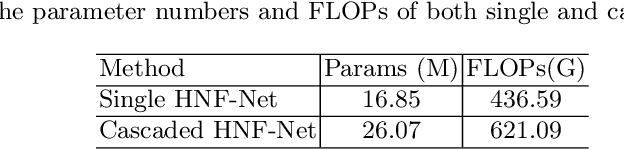
In this paper, we propose a Hybrid High-resolution and Non-local Feature Network (H2NF-Net) to segment brain tumor in multimodal MR images. Our H2NF-Net uses the single and cascaded HNF-Nets to segment different brain tumor sub-regions and combines the predictions together as the final segmentation. We trained and evaluated our model on the Multimodal Brain Tumor Segmentation Challenge (BraTS) 2020 dataset. The results on the test set show that the combination of the single and cascaded models achieved average Dice scores of 0.78751, 0.91290, and 0.85461, as well as Hausdorff distances ($95\%$) of 26.57525, 4.18426, and 4.97162 for the enhancing tumor, whole tumor, and tumor core, respectively. Our method won the second place in the BraTS 2020 challenge segmentation task out of nearly 80 participants.

CommPOOL: An Interpretable Graph Pooling Framework for Hierarchical Graph Representation Learning

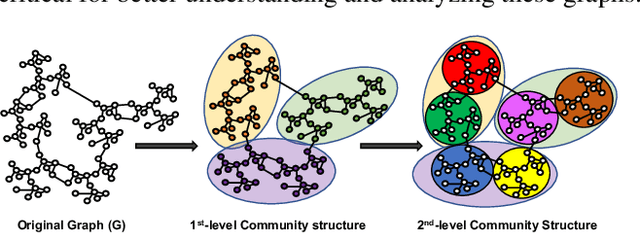
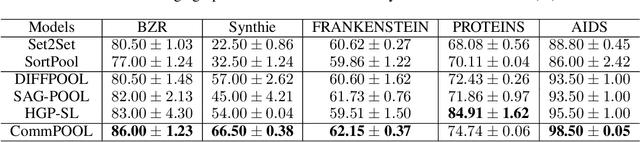
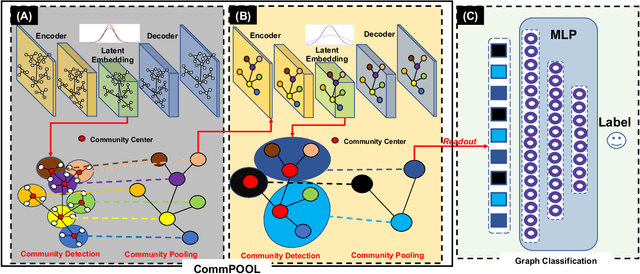
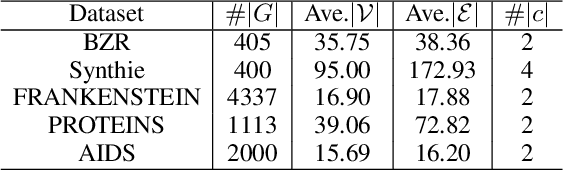
Recent years have witnessed the emergence and flourishing of hierarchical graph pooling neural networks (HGPNNs) which are effective graph representation learning approaches for graph level tasks such as graph classification. However, current HGPNNs do not take full advantage of the graph's intrinsic structures (e.g., community structure). Moreover, the pooling operations in existing HGPNNs are difficult to be interpreted. In this paper, we propose a new interpretable graph pooling framework - CommPOOL, that can capture and preserve the hierarchical community structure of graphs in the graph representation learning process. Specifically, the proposed community pooling mechanism in CommPOOL utilizes an unsupervised approach for capturing the inherent community structure of graphs in an interpretable manner. CommPOOL is a general and flexible framework for hierarchical graph representation learning that can further facilitate various graph-level tasks. Evaluations on five public benchmark datasets and one synthetic dataset demonstrate the superior performance of CommPOOL in graph representation learning for graph classification compared to the state-of-the-art baseline methods, and its effectiveness in capturing and preserving the community structure of graphs.

A Deep Drift-Diffusion Model for Image Aesthetic Score Distribution Prediction

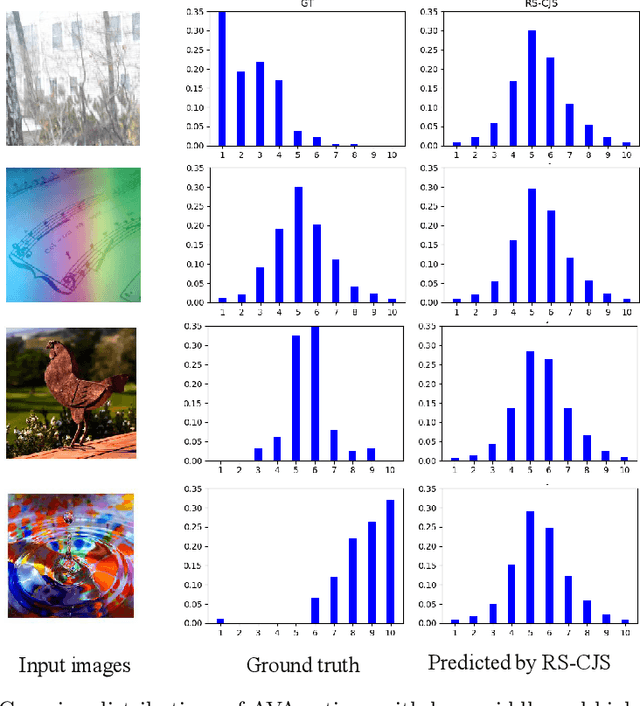
The task of aesthetic quality assessment is complicated due to its subjectivity. In recent years, the target representation of image aesthetic quality has changed from a one-dimensional binary classification label or numerical score to a multi-dimensional score distribution. According to current methods, the ground truth score distributions are straightforwardly regressed. However, the subjectivity of aesthetics is not taken into account, that is to say, the psychological processes of human beings are not taken into consideration, which limits the performance of the task. In this paper, we propose a Deep Drift-Diffusion (DDD) model inspired by psychologists to predict aesthetic score distribution from images. The DDD model can describe the psychological process of aesthetic perception instead of traditional modeling of the results of assessment. We use deep convolution neural networks to regress the parameters of the drift-diffusion model. The experimental results in large scale aesthetic image datasets reveal that our novel DDD model is simple but efficient, which outperforms the state-of-the-art methods in aesthetic score distribution prediction. Besides, different psychological processes can also be predicted by our model.

Gradient Descent Ascent for Min-Max Problems on Riemannian Manifold

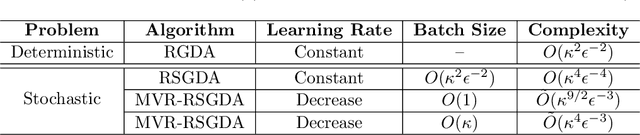
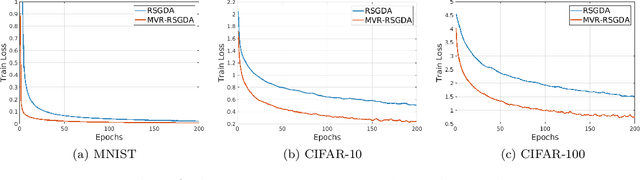
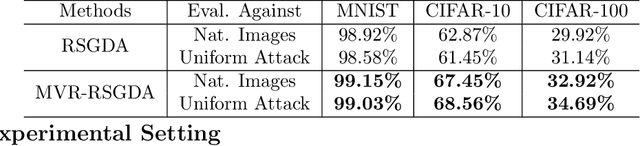
In the paper, we study a class of useful non-convex minimax optimization problems on the Riemanian manifold and propose a class of Riemanian gradient descent ascent algorithms to solve these minimax problems. Specifically, we propose a new Riemannian gradient descent ascent (RGDA) algorithm for the deterministic minimax optimization. Moreover, we prove that the RGDA has a sample complexity of $O(\kappa^2\epsilon^{-2})$ for finding an $\epsilon$-stationary point of the nonconvex strongly-concave minimax problems, where $\kappa$ denotes the condition number. At the same time, we introduce a Riemannian stochastic gradient descent ascent (RSGDA) algorithm for the stochastic minimax optimization. In the theoretical analysis, we prove that the RSGDA can achieve a sample complexity of $O(\kappa^4\epsilon^{-4})$. To further reduce the sample complexity, we propose a novel momentum variance-reduced Riemannian stochastic gradient descent ascent (MVR-RSGDA) algorithm based on a new momentum variance-reduced technique of STORM. We prove that the MVR-RSGDA algorithm achieves a lower sample complexity of $\tilde{O}(\kappa^{4}\epsilon^{-3})$ without large batches, which reaches near the best known sample complexity for its Euclidean counterparts. This is the first study of the minimax optimization over the Riemannian manifold. Extensive experimental results on the robust deep neural networks training over Stiefel manifold demonstrate the efficiency of our proposed algorithms.

Improved Bilevel Model: Fast and Optimal Algorithm with Theoretical Guarantee

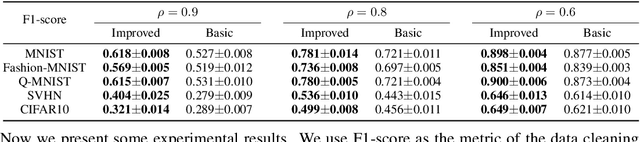
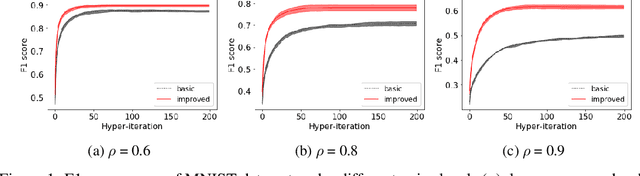
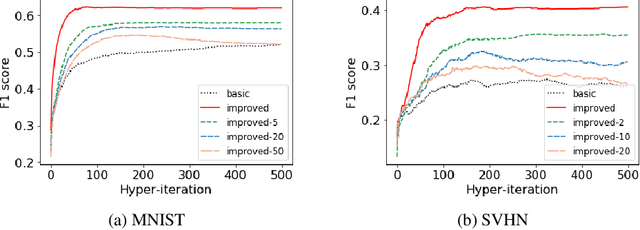
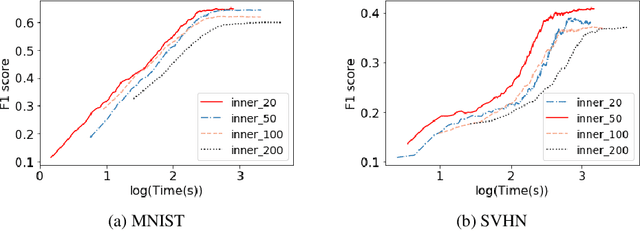
Due to the hierarchical structure of many machine learning problems, bilevel programming is becoming more and more important recently, however, the complicated correlation between the inner and outer problem makes it extremely challenging to solve. Although several intuitive algorithms based on the automatic differentiation have been proposed and obtained success in some applications, not much attention has been paid to finding the optimal formulation of the bilevel model. Whether there exists a better formulation is still an open problem. In this paper, we propose an improved bilevel model which converges faster and better compared to the current formulation. We provide theoretical guarantee and evaluation results over two tasks: Data Hyper-Cleaning and Hyper Representation Learning. The empirical results show that our model outperforms the current bilevel model with a great margin. \emph{This is a concurrent work with \citet{liu2020generic} and we submitted to ICML 2020. Now we put it on the arxiv for record.}

Periodic Stochastic Gradient Descent with Momentum for Decentralized Training

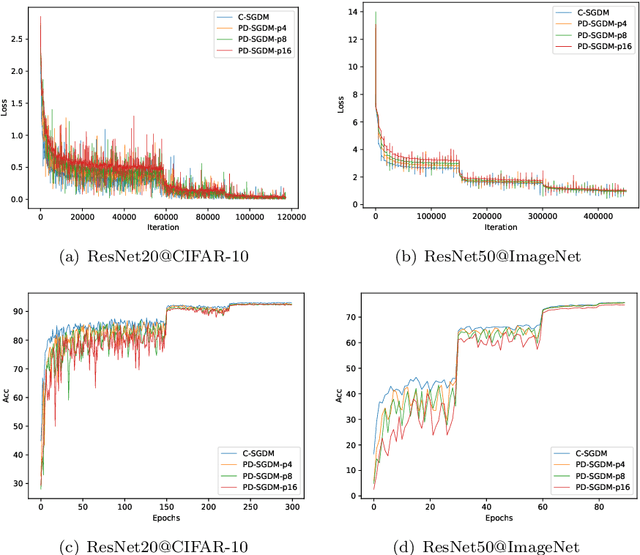
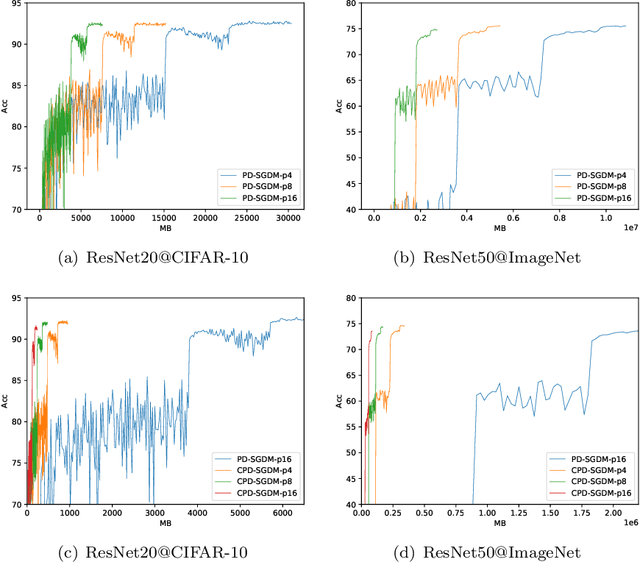
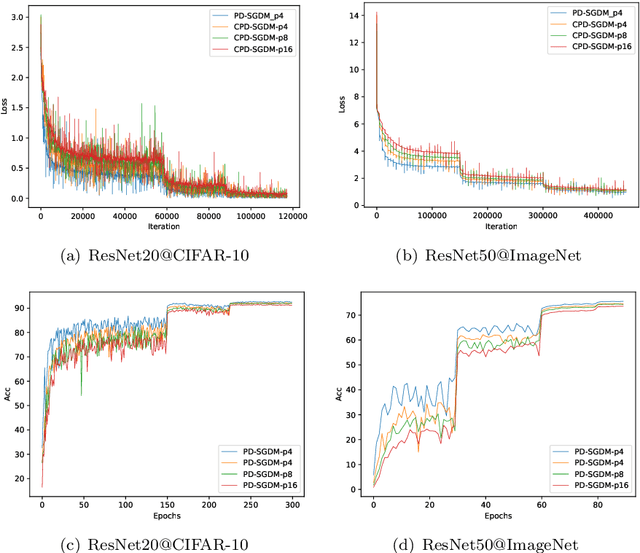
Decentralized training has been actively studied in recent years. Although a wide variety of methods have been proposed, yet the decentralized momentum SGD method is still underexplored. In this paper, we propose a novel periodic decentralized momentum SGD method, which employs the momentum schema and periodic communication for decentralized training. With these two strategies, as well as the topology of the decentralized training system, the theoretical convergence analysis of our proposed method is difficult. We address this challenging problem and provide the condition under which our proposed method can achieve the linear speedup regarding the number of workers. Furthermore, we also introduce a communication-efficient variant to reduce the communication cost in each communication round. The condition for achieving the linear speedup is also provided for this variant. To the best of our knowledge, these two methods are all the first ones achieving these theoretical results in their corresponding domain. We conduct extensive experiments to verify the performance of our proposed two methods, and both of them have shown superior performance over existing methods.

Adaptive Serverless Learning

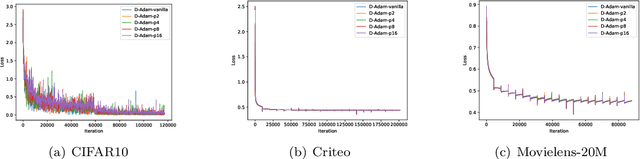
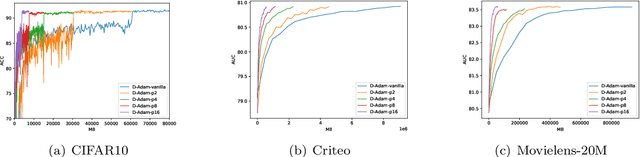
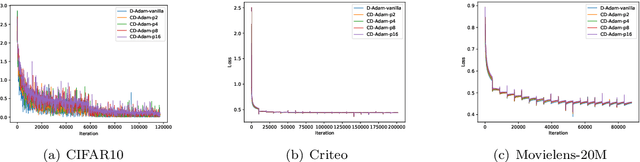
With the emergence of distributed data, training machine learning models in the serverless manner has attracted increasing attention in recent years. Numerous training approaches have been proposed in this regime, such as decentralized SGD. However, all existing decentralized algorithms only focus on standard SGD. It might not be suitable for some applications, such as deep factorization machine in which the feature is highly sparse and categorical so that the adaptive training algorithm is needed. In this paper, we propose a novel adaptive decentralized training approach, which can compute the learning rate from data dynamically. To the best of our knowledge, this is the first adaptive decentralized training approach. Our theoretical results reveal that the proposed algorithm can achieve linear speedup with respect to the number of workers. Moreover, to reduce the communication-efficient overhead, we further propose a communication-efficient adaptive decentralized training approach, which can also achieve linear speedup with respect to the number of workers. At last, extensive experiments on different tasks have confirmed the effectiveness of our proposed two approaches.

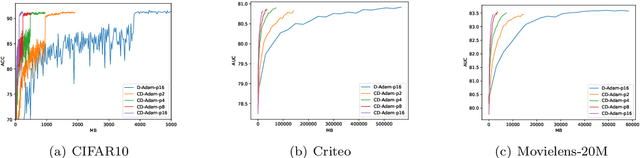
Accelerated Zeroth-Order Momentum Methods from Mini to Minimax Optimization

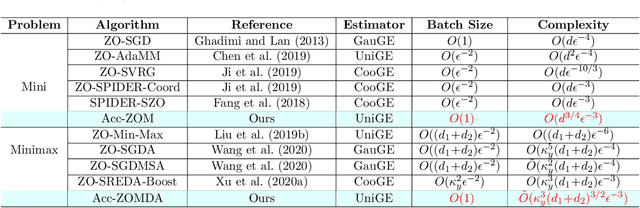
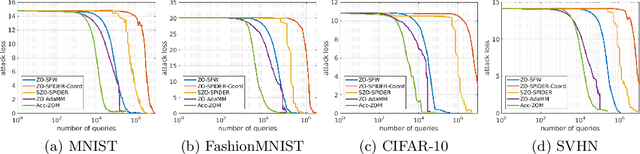
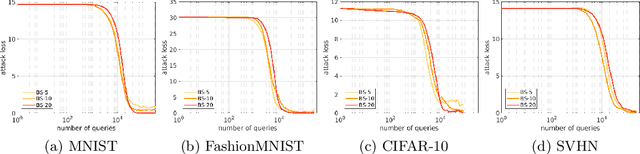
In the paper, we propose a new accelerated zeroth-order momentum (Acc-ZOM) method to solve the non-convex stochastic mini-optimization problems. We prove that the Acc-ZOM method achieves a lower query complexity of $O(d^{3/4}\epsilon^{-3})$ for finding an $\epsilon$-stationary point, which improves the best known result by a factor of $O(d^{1/4})$ where $d$ denotes the parameter dimension. The Acc-ZOM does not require any batches compared to the large batches required in the existing zeroth-order stochastic algorithms. Further, we extend the Acc-ZOM method to solve the non-convex stochastic minimax-optimization problems and propose an accelerated zeroth-order momentum descent ascent (Acc-ZOMDA) method. We prove that the Acc-ZOMDA method reaches the best know query complexity of $\tilde{O}(\kappa_y^3(d_1+d_2)^{3/2}\epsilon^{-3})$ for finding an $\epsilon$-stationary point, where $d_1$ and $d_2$ denote dimensions of the mini and max optimization parameters respectively and $\kappa_y$ is condition number. In particular, our theoretical result does not rely on large batches required in the existing methods. Moreover, we propose a momentum-based accelerated framework for the minimax-optimization problems. At the same time, we present an accelerated momentum descent ascent (Acc-MDA) method for solving the white-box minimax problems, and prove that it achieves the best known gradient complexity of $\tilde{O}(\kappa_y^3\epsilon^{-3})$ without large batches. Extensive experimental results on the black-box adversarial attack to deep neural networks (DNNs) and poisoning attack demonstrate the efficiency of our algorithms.