Optimizing Generalized Rate Metrics through Game Equilibrium

We present a general framework for solving a large class of learning problems with non-linear functions of classification rates. This includes problems where one wishes to optimize a non-decomposable performance metric such as the F-measure or G-mean, and constrained training problems where the classifier needs to satisfy non-linear rate constraints such as predictive parity fairness, distribution divergences or churn ratios. We extend previous two-player game approaches for constrained optimization to a game between three players to decouple the classifier rates from the non-linear objective, and seek to find an equilibrium of the game. Our approach generalizes many existing algorithms, and makes possible new algorithms with more flexibility and tighter handling of non-linear rate constraints. We provide convergence guarantees for convex functions of rates, and show how our methodology can be extended to handle sums of ratios of rates. Experiments on different fairness tasks confirm the efficacy of our approach.

Pairwise Fairness for Ranking and Regression

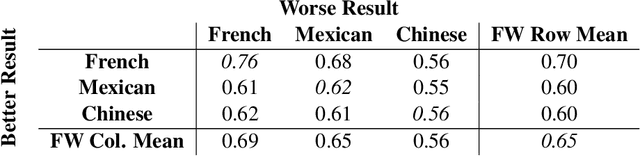
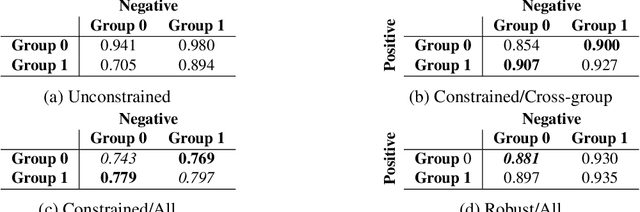
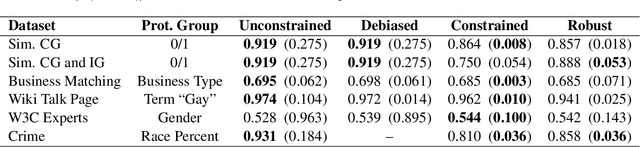
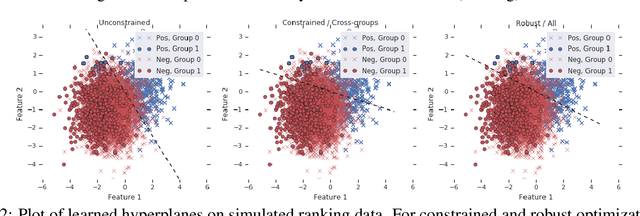
We present pairwise metrics of fairness for ranking and regression models that form analogues of statistical fairness notions such as equal opportunity or equal accuracy, as well as statistical parity. Our pairwise formulation supports both discrete protected groups, and continuous protected attributes. We show that the resulting training problems can be efficiently and effectively solved using constrained optimization and robust optimization techniques based on two player game algorithms developed for fair classification. Experiments illustrate the broad applicability and trade-offs of these methods.

Optimal Auctions through Deep Learning

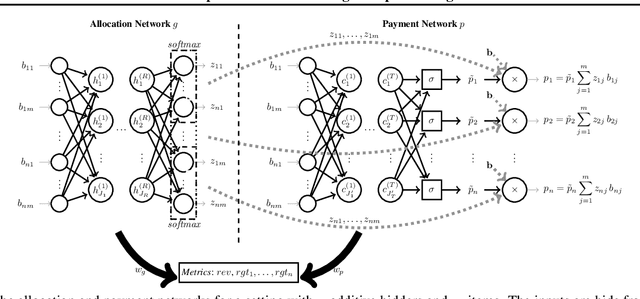
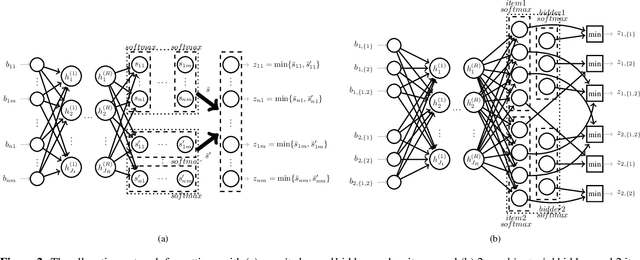
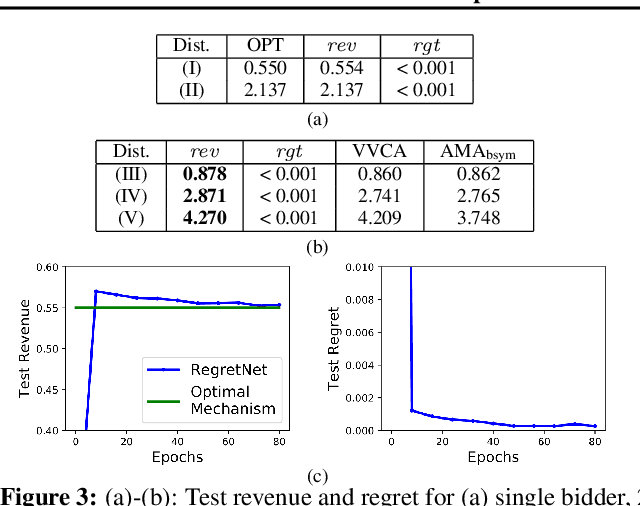
Designing an auction that maximizes expected revenue is an intricate task. Indeed, as of today--despite major efforts and impressive progress over the past few years--only the single-item case is fully understood. In this work, we initiate the exploration of the use of tools from deep learning on this topic. The design objective is revenue optimal, dominant-strategy incentive compatible auctions. We show that multi-layer neural networks can learn almost-optimal auctions for settings for which there are analytical solutions, such as Myerson's auction for a single item, Manelli and Vincent's mechanism for a single bidder with additive preferences over two items, or Yao's auction for two additive bidders with binary support distributions and multiple items, even if no prior knowledge about the form of optimal auctions is encoded in the network and the only feedback during training is revenue and regret. We further show how characterization results, even rather implicit ones such as Rochet's characterization through induced utilities and their gradients, can be leveraged to obtain more precise fits to the optimal design. We conclude by demonstrating the potential of deep learning for deriving optimal auctions with high revenue for poorly understood problems.

Online Optimization Methods for the Quantification Problem

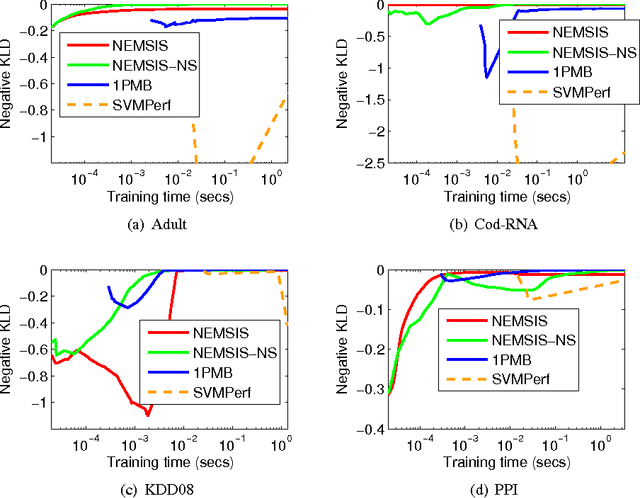
The estimation of class prevalence, i.e., the fraction of a population that belongs to a certain class, is a very useful tool in data analytics and learning, and finds applications in many domains such as sentiment analysis, epidemiology, etc. For example, in sentiment analysis, the objective is often not to estimate whether a specific text conveys a positive or a negative sentiment, but rather estimate the overall distribution of positive and negative sentiments during an event window. A popular way of performing the above task, often dubbed quantification, is to use supervised learning to train a prevalence estimator from labeled data. Contemporary literature cites several performance measures used to measure the success of such prevalence estimators. In this paper we propose the first online stochastic algorithms for directly optimizing these quantification-specific performance measures. We also provide algorithms that optimize hybrid performance measures that seek to balance quantification and classification performance. Our algorithms present a significant advancement in the theory of multivariate optimization and we show, by a rigorous theoretical analysis, that they exhibit optimal convergence. We also report extensive experiments on benchmark and real data sets which demonstrate that our methods significantly outperform existing optimization techniques used for these performance measures.

Support Vector Algorithms for Optimizing the Partial Area Under the ROC Curve

The area under the ROC curve (AUC) is a widely used performance measure in machine learning. Increasingly, however, in several applications, ranging from ranking to biometric screening to medicine, performance is measured not in terms of the full area under the ROC curve, but in terms of the \emph{partial} area under the ROC curve between two false positive rates. In this paper, we develop support vector algorithms for directly optimizing the partial AUC between any two false positive rates. Our methods are based on minimizing a suitable proxy or surrogate objective for the partial AUC error. In the case of the full AUC, one can readily construct and optimize convex surrogates by expressing the performance measure as a summation of pairwise terms. The partial AUC, on the other hand, does not admit such a simple decomposable structure, making it more challenging to design and optimize (tight) convex surrogates for this measure. Our approach builds on the structural SVM framework of Joachims (2005) to design convex surrogates for partial AUC, and solves the resulting optimization problem using a cutting plane solver. Unlike the full AUC, where the combinatorial optimization needed in each iteration of the cutting plane solver can be decomposed and solved efficiently, the corresponding problem for the partial AUC is harder to decompose. One of our main contributions is a polynomial time algorithm for solving the combinatorial optimization problem associated with partial AUC. We also develop an approach for optimizing a tighter non-convex hinge loss based surrogate for the partial AUC using difference-of-convex programming. Our experiments on a variety of real-world and benchmark tasks confirm the efficacy of the proposed methods.

Surrogate Functions for Maximizing Precision at the Top

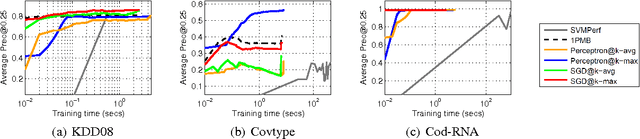
The problem of maximizing precision at the top of a ranked list, often dubbed Precision@k (prec@k), finds relevance in myriad learning applications such as ranking, multi-label classification, and learning with severe label imbalance. However, despite its popularity, there exist significant gaps in our understanding of this problem and its associated performance measure. The most notable of these is the lack of a convex upper bounding surrogate for prec@k. We also lack scalable perceptron and stochastic gradient descent algorithms for optimizing this performance measure. In this paper we make key contributions in these directions. At the heart of our results is a family of truly upper bounding surrogates for prec@k. These surrogates are motivated in a principled manner and enjoy attractive properties such as consistency to prec@k under various natural margin/noise conditions. These surrogates are then used to design a class of novel perceptron algorithms for optimizing prec@k with provable mistake bounds. We also devise scalable stochastic gradient descent style methods for this problem with provable convergence bounds. Our proofs rely on novel uniform convergence bounds which require an in-depth analysis of the structural properties of prec@k and its surrogates. We conclude with experimental results comparing our algorithms with state-of-the-art cutting plane and stochastic gradient algorithms for maximizing prec@k.

Optimizing Non-decomposable Performance Measures: A Tale of Two Classes

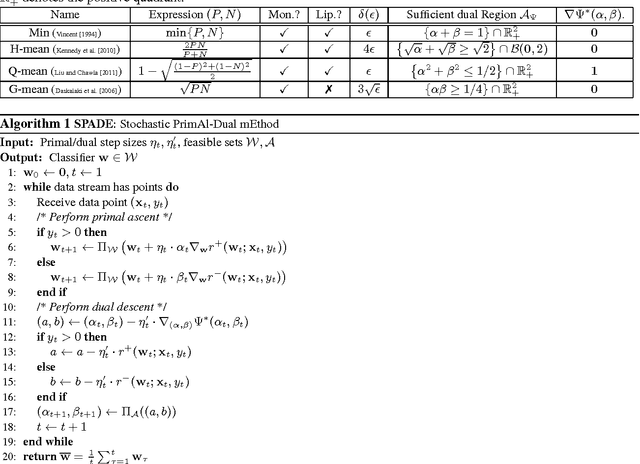
Modern classification problems frequently present mild to severe label imbalance as well as specific requirements on classification characteristics, and require optimizing performance measures that are non-decomposable over the dataset, such as F-measure. Such measures have spurred much interest and pose specific challenges to learning algorithms since their non-additive nature precludes a direct application of well-studied large scale optimization methods such as stochastic gradient descent. In this paper we reveal that for two large families of performance measures that can be expressed as functions of true positive/negative rates, it is indeed possible to implement point stochastic updates. The families we consider are concave and pseudo-linear functions of TPR, TNR which cover several popularly used performance measures such as F-measure, G-mean and H-mean. Our core contribution is an adaptive linearization scheme for these families, using which we develop optimization techniques that enable truly point-based stochastic updates. For concave performance measures we propose SPADE, a stochastic primal dual solver; for pseudo-linear measures we propose STAMP, a stochastic alternate maximization procedure. Both methods have crisp convergence guarantees, demonstrate significant speedups over existing methods - often by an order of magnitude or more, and give similar or more accurate predictions on test data.

Consistent Classification Algorithms for Multi-class Non-Decomposable Performance Metrics

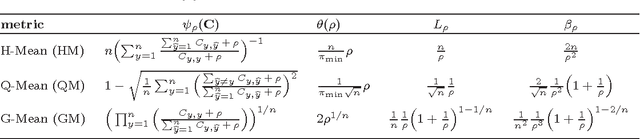
We study consistency of learning algorithms for a multi-class performance metric that is a non-decomposable function of the confusion matrix of a classifier and cannot be expressed as a sum of losses on individual data points; examples of such performance metrics include the macro F-measure popular in information retrieval and the G-mean metric used in class-imbalanced problems. While there has been much work in recent years in understanding the consistency properties of learning algorithms for `binary' non-decomposable metrics, little is known either about the form of the optimal classifier for a general multi-class non-decomposable metric, or about how these learning algorithms generalize to the multi-class case. In this paper, we provide a unified framework for analysing a multi-class non-decomposable performance metric, where the problem of finding the optimal classifier for the performance metric is viewed as an optimization problem over the space of all confusion matrices achievable under the given distribution. Using this framework, we show that (under a continuous distribution) the optimal classifier for a multi-class performance metric can be obtained as the solution of a cost-sensitive classification problem, thus generalizing several previous results on specific binary non-decomposable metrics. We then design a consistent learning algorithm for concave multi-class performance metrics that proceeds via a sequence of cost-sensitive classification problems, and can be seen as applying the conditional gradient (CG) optimization method over the space of feasible confusion matrices. To our knowledge, this is the first efficient learning algorithm (whose running time is polynomial in the number of classes) that is consistent for a large family of multi-class non-decomposable metrics. Our consistency proof uses a novel technique based on the convergence analysis of the CG method.

Online and Stochastic Gradient Methods for Non-decomposable Loss Functions

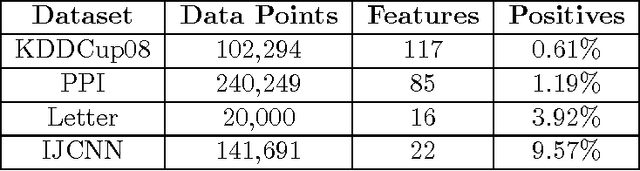
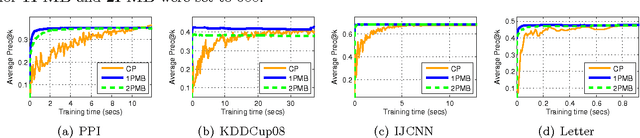
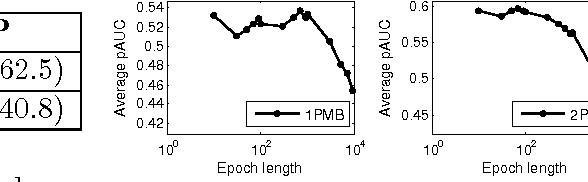
Modern applications in sensitive domains such as biometrics and medicine frequently require the use of non-decomposable loss functions such as precision@k, F-measure etc. Compared to point loss functions such as hinge-loss, these offer much more fine grained control over prediction, but at the same time present novel challenges in terms of algorithm design and analysis. In this work we initiate a study of online learning techniques for such non-decomposable loss functions with an aim to enable incremental learning as well as design scalable solvers for batch problems. To this end, we propose an online learning framework for such loss functions. Our model enjoys several nice properties, chief amongst them being the existence of efficient online learning algorithms with sublinear regret and online to batch conversion bounds. Our model is a provable extension of existing online learning models for point loss functions. We instantiate two popular losses, prec@k and pAUC, in our model and prove sublinear regret bounds for both of them. Our proofs require a novel structural lemma over ranked lists which may be of independent interest. We then develop scalable stochastic gradient descent solvers for non-decomposable loss functions. We show that for a large family of loss functions satisfying a certain uniform convergence property (that includes prec@k, pAUC, and F-measure), our methods provably converge to the empirical risk minimizer. Such uniform convergence results were not known for these losses and we establish these using novel proof techniques. We then use extensive experimentation on real life and benchmark datasets to establish that our method can be orders of magnitude faster than a recently proposed cutting plane method.