A Distributed Block Chebyshev-Davidson Algorithm for Parallel Spectral Clustering

We develop a distributed Block Chebyshev-Davidson algorithm to solve large-scale leading eigenvalue problems for spectral analysis in spectral clustering. First, the efficiency of the Chebyshev-Davidson algorithm relies on the prior knowledge of the eigenvalue spectrum, which could be expensive to estimate. This issue can be lessened by the analytic spectrum estimation of the Laplacian or normalized Laplacian matrices in spectral clustering, making the proposed algorithm very efficient for spectral clustering. Second, to make the proposed algorithm capable of analyzing big data, a distributed and parallel version has been developed with attractive scalability. The speedup by parallel computing is approximately equivalent to $\sqrt{p}$, where $p$ denotes the number of processes. Numerical results will be provided to demonstrate its efficiency and advantage over existing algorithms in both sequential and parallel computing.

What is the Solution for State-Adversarial Multi-Agent Reinforcement Learning?

Various types of Multi-Agent Reinforcement Learning (MARL) methods have been developed, assuming that agents' policies are based on true states. Recent works have improved the robustness of MARL under uncertainties from the reward, transition probability, or other partners' policies. However, in real-world multi-agent systems, state estimations may be perturbed by sensor measurement noise or even adversaries. Agents' policies trained with only true state information will deviate from optimal solutions when facing adversarial state perturbations during execution. MARL under adversarial state perturbations has limited study. Hence, in this work, we propose a State-Adversarial Markov Game (SAMG) and make the first attempt to study the fundamental properties of MARL under state uncertainties. We prove that the optimal agent policy and the robust Nash equilibrium do not always exist for an SAMG. Instead, we define the solution concept, robust agent policy, of the proposed SAMG under adversarial state perturbations, where agents want to maximize the worst-case expected state value. We then design a gradient descent ascent-based robust MARL algorithm to learn the robust policies for the MARL agents. Our experiments show that adversarial state perturbations decrease agents' rewards for several baselines from the existing literature, while our algorithm outperforms baselines with state perturbations and significantly improves the robustness of the MARL policies under state uncertainties.

Accelerating Numerical Solvers for Large-Scale Simulation of Dynamical System via NeurVec

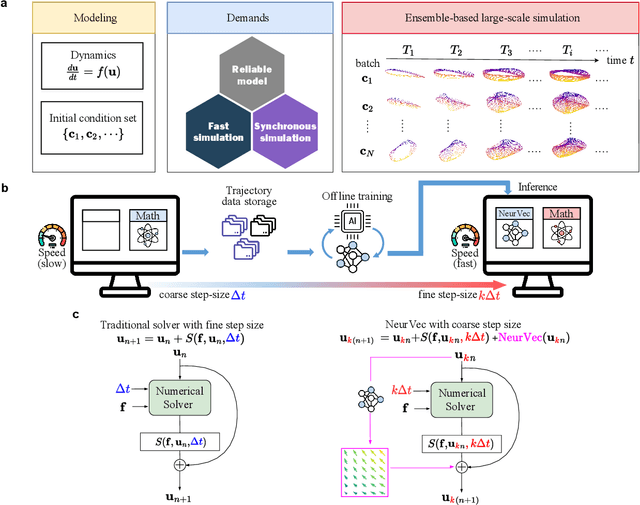
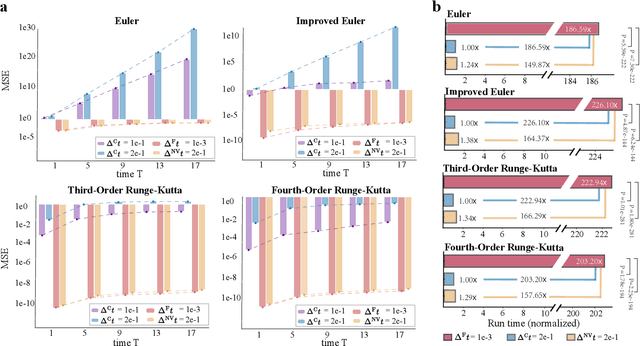
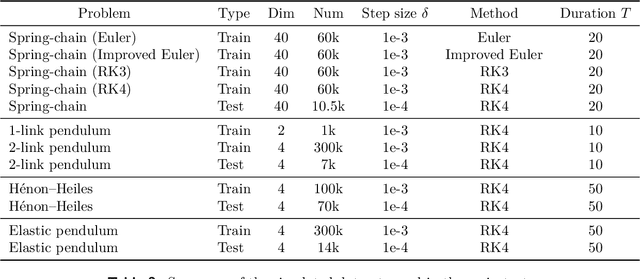
Ensemble-based large-scale simulation of dynamical systems is essential to a wide range of science and engineering problems. Conventional numerical solvers used in the simulation are significantly limited by the step size for time integration, which hampers efficiency and feasibility especially when high accuracy is desired. To overcome this limitation, we propose a data-driven corrector method that allows using large step sizes while compensating for the integration error for high accuracy. This corrector is represented in the form of a vector-valued function and is modeled by a neural network to regress the error in the phase space. Hence we name the corrector neural vector (NeurVec). We show that NeurVec can achieve the same accuracy as traditional solvers with much larger step sizes. We empirically demonstrate that NeurVec can accelerate a variety of numerical solvers significantly and overcome the stability restriction of these solvers. Our results on benchmark problems, ranging from high-dimensional problems to chaotic systems, suggest that NeurVec is capable of capturing the leading error term and maintaining the statistics of ensemble forecasts.

The Lottery Ticket Hypothesis for Self-attention in Convolutional Neural Network

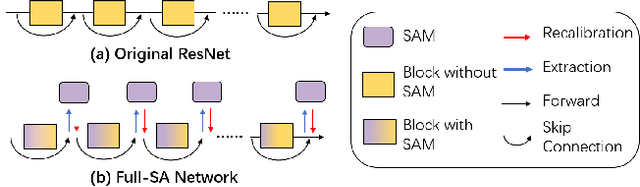
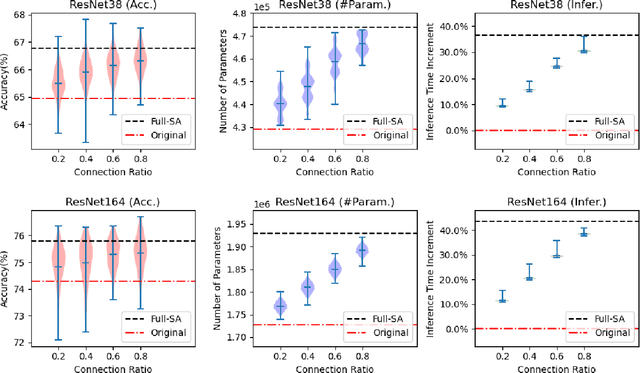
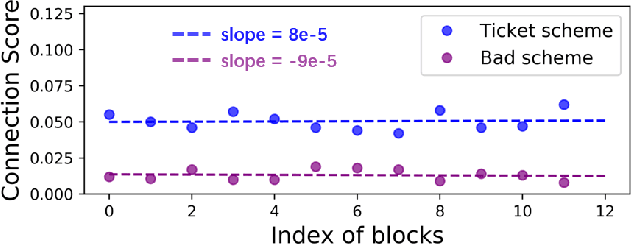
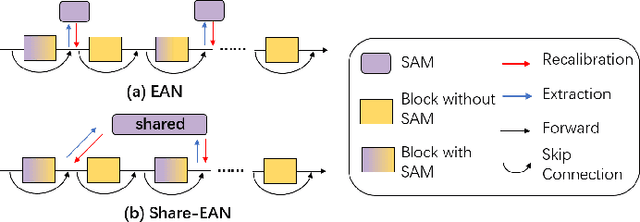
Recently many plug-and-play self-attention modules (SAMs) are proposed to enhance the model generalization by exploiting the internal information of deep convolutional neural networks (CNNs). In general, previous works ignore where to plug in the SAMs since they connect the SAMs individually with each block of the entire CNN backbone for granted, leading to incremental computational cost and the number of parameters with the growth of network depth. However, we empirically find and verify some counterintuitive phenomena that: (a) Connecting the SAMs to all the blocks may not always bring the largest performance boost, and connecting to partial blocks would be even better; (b) Adding the SAMs to a CNN may not always bring a performance boost, and instead it may even harm the performance of the original CNN backbone. Therefore, we articulate and demonstrate the Lottery Ticket Hypothesis for Self-attention Networks: a full self-attention network contains a subnetwork with sparse self-attention connections that can (1) accelerate inference, (2) reduce extra parameter increment, and (3) maintain accuracy. In addition to the empirical evidence, this hypothesis is also supported by our theoretical evidence. Furthermore, we propose a simple yet effective reinforcement-learning-based method to search the ticket, i.e., the connection scheme that satisfies the three above-mentioned conditions. Extensive experiments on widely-used benchmark datasets and popular self-attention networks show the effectiveness of our method. Besides, our experiments illustrate that our searched ticket has the capacity of transferring to some vision tasks, e.g., crowd counting and segmentation.

Finite Expression Method for Solving High-Dimensional Partial Differential Equations

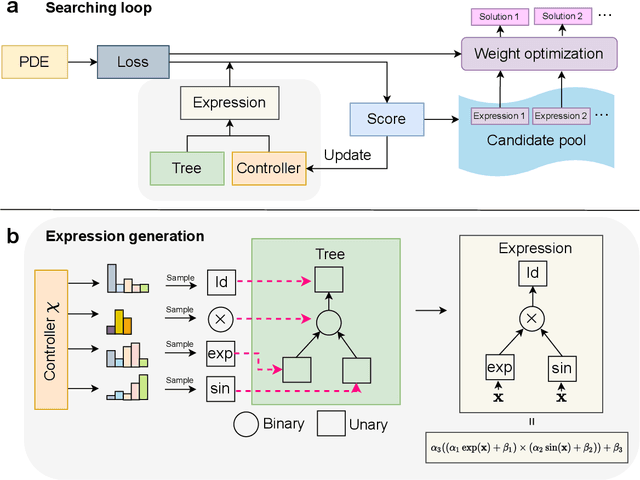
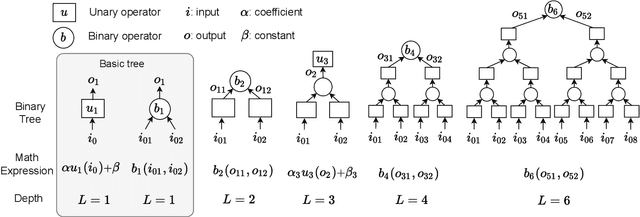
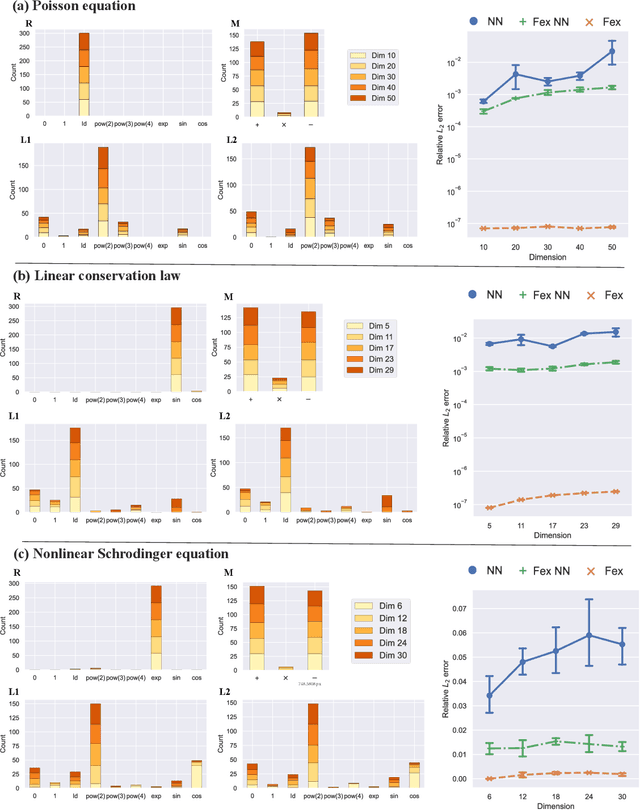
Designing efficient and accurate numerical solvers for high-dimensional partial differential equations (PDEs) remains a challenging and important topic in computational science and engineering, mainly due to the ``curse of dimensionality" in designing numerical schemes that scale in dimension. This paper introduces a new methodology that seeks an approximate PDE solution in the space of functions with finitely many analytic expressions and, hence, this methodology is named the finite expression method (FEX). It is proved in approximation theory that FEX can avoid the curse of dimensionality. As a proof of concept, a deep reinforcement learning method is proposed to implement FEX for various high-dimensional PDEs in different dimensions, achieving high and even machine accuracy with a memory complexity polynomial in dimension and an amenable time complexity. An approximate solution with finite analytic expressions also provides interpretable insights into the ground truth PDE solution, which can further help to advance the understanding of physical systems and design postprocessing techniques for a refined solution.

Reinforced Inverse Scattering

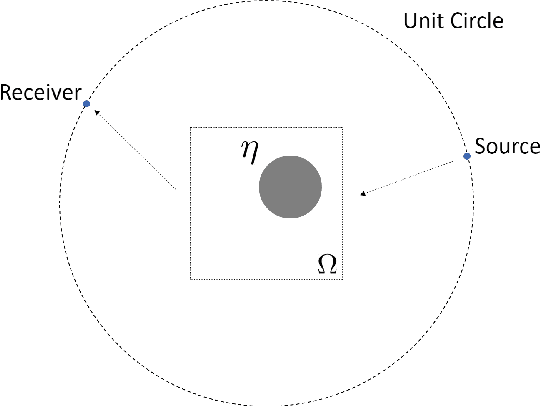
Inverse wave scattering aims at determining the properties of an object using data on how the object scatters incoming waves. In order to collect information, sensors are put in different locations to send and receive waves from each other. The choice of sensor positions and incident wave frequencies determines the reconstruction quality of scatterer properties. This paper introduces reinforcement learning to develop precision imaging that decides sensor positions and wave frequencies adaptive to different scatterers in an intelligent way, thus obtaining a significant improvement in reconstruction quality with limited imaging resources. Extensive numerical results will be provided to demonstrate the superiority of the proposed method over existing methods.

Neural Network Architecture Beyond Width and Depth

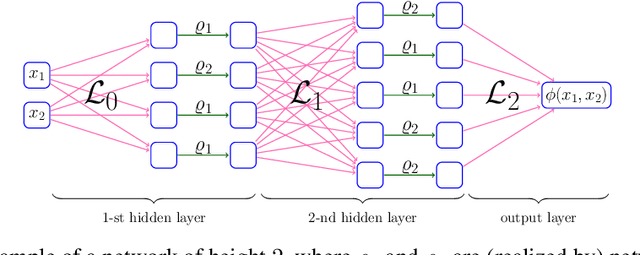
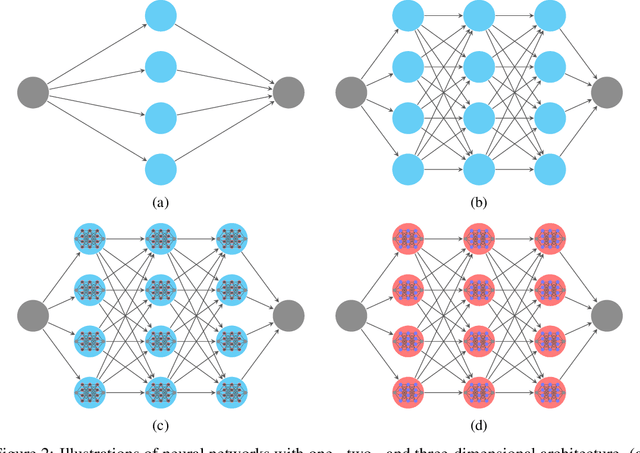
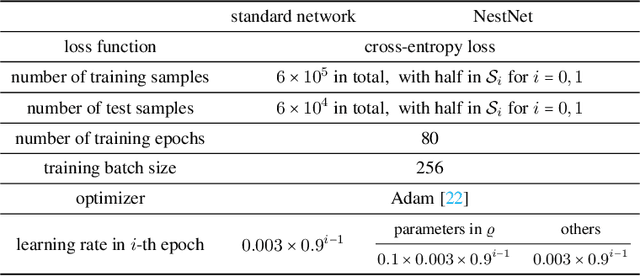
This paper proposes a new neural network architecture by introducing an additional dimension called height beyond width and depth. Neural network architectures with height, width, and depth as hyperparameters are called three-dimensional architectures. It is shown that neural networks with three-dimensional architectures are significantly more expressive than the ones with two-dimensional architectures (those with only width and depth as hyperparameters), e.g., standard fully connected networks. The new network architecture is constructed recursively via a nested structure, and hence we call a network with the new architecture nested network (NestNet). A NestNet of height $s$ is built with each hidden neuron activated by a NestNet of height $\le s-1$. When $s=1$, a NestNet degenerates to a standard network with a two-dimensional architecture. It is proved by construction that height-$s$ ReLU NestNets with $\mathcal{O}(n)$ parameters can approximate Lipschitz continuous functions on $[0,1]^d$ with an error $\mathcal{O}(n^{-(s+1)/d})$, while the optimal approximation error of standard ReLU networks with $\mathcal{O}(n)$ parameters is $\mathcal{O}(n^{-2/d})$. Furthermore, such a result is extended to generic continuous functions on $[0,1]^d$ with the approximation error characterized by the modulus of continuity. Finally, a numerical example is provided to explore the advantages of the super approximation power of ReLU NestNets.

IAE-Net: Integral Autoencoders for Discretization-Invariant Learning

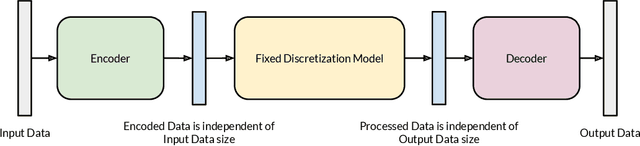
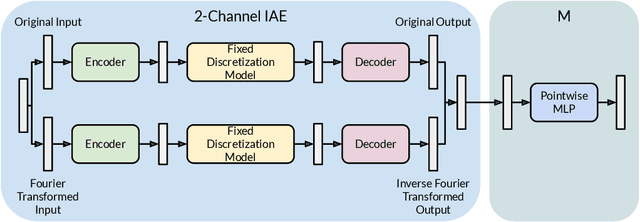
Discretization invariant learning aims at learning in the infinite-dimensional function spaces with the capacity to process heterogeneous discrete representations of functions as inputs and/or outputs of a learning model. This paper proposes a novel deep learning framework based on integral autoencoders (IAE-Net) for discretization invariant learning. The basic building block of IAE-Net consists of an encoder and a decoder as integral transforms with data-driven kernels, and a fully connected neural network between the encoder and decoder. This basic building block is applied in parallel in a wide multi-channel structure, which are repeatedly composed to form a deep and densely connected neural network with skip connections as IAE-Net. IAE-Net is trained with randomized data augmentation that generates training data with heterogeneous structures to facilitate the performance of discretization invariant learning. The proposed IAE-Net is tested with various applications in predictive data science, solving forward and inverse problems in scientific computing, and signal/image processing. Compared with alternatives in the literature, IAE-Net achieves state-of-the-art performance in existing applications and creates a wide range of new applications.

Connecting Optimization and Generalization via Gradient Flow Path Length

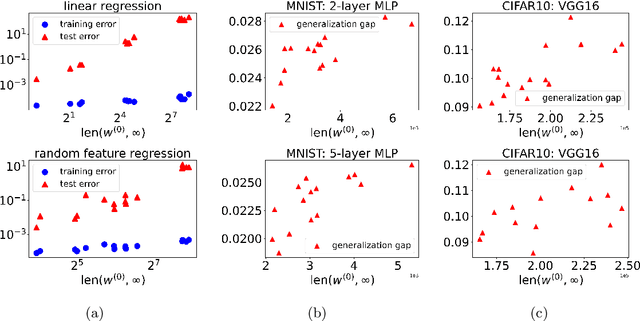
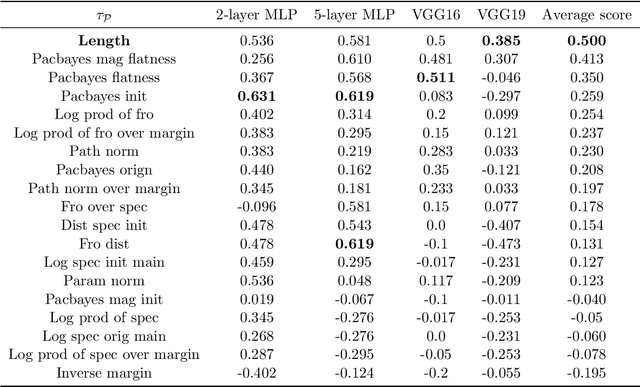
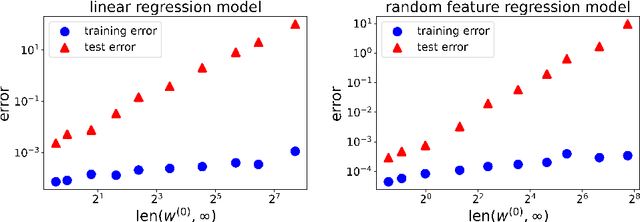
Optimization and generalization are two essential aspects of machine learning. In this paper, we propose a framework to connect optimization with generalization by analyzing the generalization error based on the length of optimization trajectory under the gradient flow algorithm after convergence. Through our approach, we show that, with a proper initialization, gradient flow converges following a short path with an explicit length estimate. Such an estimate induces a length-based generalization bound, showing that short optimization paths after convergence are associated with good generalization, which also matches our numerical results. Our framework can be applied to broad settings. For example, we use it to obtain generalization estimates on three distinct machine learning models: underdetermined $\ell_p$ linear regression, kernel regression, and overparameterized two-layer ReLU neural networks.

Deep Nonparametric Estimation of Operators between Infinite Dimensional Spaces

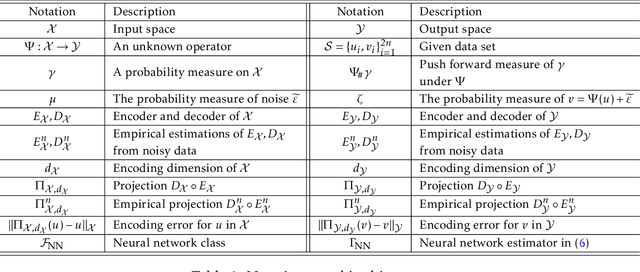
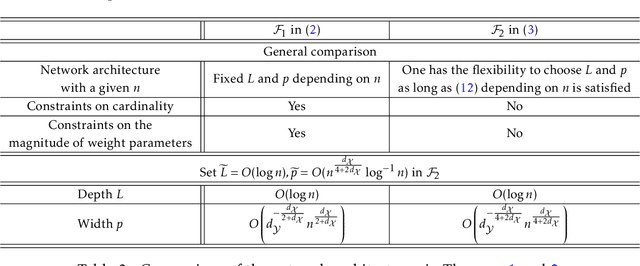
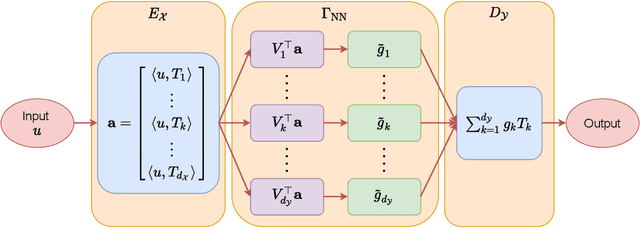
Learning operators between infinitely dimensional spaces is an important learning task arising in wide applications in machine learning, imaging science, mathematical modeling and simulations, etc. This paper studies the nonparametric estimation of Lipschitz operators using deep neural networks. Non-asymptotic upper bounds are derived for the generalization error of the empirical risk minimizer over a properly chosen network class. Under the assumption that the target operator exhibits a low dimensional structure, our error bounds decay as the training sample size increases, with an attractive fast rate depending on the intrinsic dimension in our estimation. Our assumptions cover most scenarios in real applications and our results give rise to fast rates by exploiting low dimensional structures of data in operator estimation. We also investigate the influence of network structures (e.g., network width, depth, and sparsity) on the generalization error of the neural network estimator and propose a general suggestion on the choice of network structures to maximize the learning efficiency quantitatively.