RPWithPrior: Label Differential Privacy in Regression

With the wide application of machine learning techniques in practice, privacy preservation has gained increasing attention. Protecting user privacy with minimal accuracy loss is a fundamental task in the data analysis and mining community. In this paper, we focus on regression tasks under $ε$-label differential privacy guarantees. Some existing methods for regression with $ε$-label differential privacy, such as the RR-On-Bins mechanism, discretized the output space into finite bins and then applied RR algorithm. To efficiently determine these finite bins, the authors rounded the original responses down to integer values. However, such operations does not align well with real-world scenarios. To overcome these limitations, we model both original and randomized responses as continuous random variables, avoiding discretization entirely. Our novel approach estimates an optimal interval for randomized responses and introduces new algorithms designed for scenarios where a prior is either known or unknown. Additionally, we prove that our algorithm, RPWithPrior, guarantees $ε$-label differential privacy. Numerical results demonstrate that our approach gets better performance compared with the Gaussian, Laplace, Staircase, and RRonBins, Unbiased mechanisms on the Communities and Crime, Criteo Sponsored Search Conversion Log, California Housing datasets.

Improving Classifier-Free Guidance of Flow Matching via Manifold Projection

Classifier-free guidance (CFG) is a widely used technique for controllable generation in diffusion and flow-based models. Despite its empirical success, CFG relies on a heuristic linear extrapolation that is often sensitive to the guidance scale. In this work, we provide a principled interpretation of CFG through the lens of optimization. We demonstrate that the velocity field in flow matching corresponds to the gradient of a sequence of smoothed distance functions, which guides latent variables toward the scaled target image set. This perspective reveals that the standard CFG formulation is an approximation of this gradient, where the prediction gap, the discrepancy between conditional and unconditional outputs, governs guidance sensitivity. Leveraging this insight, we reformulate the CFG sampling as a homotopy optimization with a manifold constraint. This formulation necessitates a manifold projection step, which we implement via an incremental gradient descent scheme during sampling. To improve computational efficiency and stability, we further enhance this iterative process with Anderson Acceleration without requiring additional model evaluations. Our proposed methods are training-free and consistently refine generation fidelity, prompt alignment, and robustness to the guidance scale. We validate their effectiveness across diverse benchmarks, demonstrating significant improvements on large-scale models such as DiT-XL-2-256, Flux, and Stable Diffusion 3.5.

Learning with Noisy Labels: the Exploration of Error Bounds in Classification

Numerous studies have shown that label noise can lead to poor generalization performance, negatively affecting classification accuracy. Therefore, understanding the effectiveness of classifiers trained using deep neural networks in the presence of noisy labels is of considerable practical significance. In this paper, we focus on the error bounds of excess risks for classification problems with noisy labels within deep learning frameworks. We begin by exploring loss functions with noise-tolerant properties, ensuring that the empirical minimizer on noisy data aligns with that on the true data. Next, we estimate the error bounds of the excess risks, expressed as a sum of statistical error and approximation error. We estimate the statistical error on a dependent (mixing) sequence, bounding it with the help of the associated independent block sequence. For the approximation error, we first express the classifiers as the composition of the softmax function and a continuous function from $[0,1]^d$ to $\mathbb{R}^K$. The main task is then to estimate the approximation error for the continuous function from $[0,1]^d$ to $\mathbb{R}^K$. Finally, we focus on the curse of dimensionality based on the low-dimensional manifold assumption.

MAP-based Problem-Agnostic diffusion model for Inverse Problems

Diffusion models have indeed shown great promise in solving inverse problems in image processing. In this paper, we propose a novel, problem-agnostic diffusion model called the maximum a posteriori (MAP)-based guided term estimation method for inverse problems. We divide the conditional score function into two terms according to Bayes' rule: the unconditional score function and the guided term. We design the MAP-based guided term estimation method, while the unconditional score function is approximated by an existing score network. To estimate the guided term, we base on the assumption that the space of clean natural images is inherently smooth, and introduce a MAP estimate of the $t$-th latent variable. We then substitute this estimation into the expression of the inverse problem and obtain the approximation of the guided term. We evaluate our method extensively on super-resolution, inpainting, and denoising tasks, and demonstrate comparable performance to DDRM, DMPS, DPS and $\Pi$GDM.

Bridging Fairness Gaps: A (Conditional) Distance Covariance Perspective in Fairness Learning

We bridge fairness gaps from a statistical perspective by selectively utilizing either conditional distance covariance or distance covariance statistics as measures to assess the independence between predictions and sensitive attributes. We enhance fairness by incorporating sample (conditional) distance covariance as a manageable penalty term into the machine learning process. Additionally, we present the matrix form of empirical (conditional) distance covariance for parallel calculations to enhance computational efficiency. Theoretically, we provide a proof for the convergence between empirical and population (conditional) distance covariance, establishing necessary guarantees for batch computations. Through experiments conducted on a range of real-world datasets, we have demonstrated that our method effectively bridges the fairness gap in machine learning.

The Exploration of Neural Collapse under Imbalanced Data

Neural collapse, a newly identified characteristic, describes a property of solutions during model training. In this paper, we explore neural collapse in the context of imbalanced data. We consider the $L$-extended unconstrained feature model with a bias term and provide a theoretical analysis of global minimizer. Our findings include: (1) Features within the same class converge to their class mean, similar to both the balanced case and the imbalanced case without bias. (2) The geometric structure is mainly on the left orthonormal transformation of the product of $L$ linear classifiers and the right transformation of the class-mean matrix. (3) Some rows of the left orthonormal transformation of the product of $L$ linear classifiers collapse to zeros and others are orthogonal, which relies on the singular values of $\hat Y=(I_K-1/N\mathbf{n}1^\top_K)D$, where $K$ is class size, $\mathbf{n}$ is the vector of sample size for each class, $D$ is the diagonal matrix whose diagonal entries are given by $\sqrt{\mathbf{n}}$. Similar results are for the columns of the right orthonormal transformation of the product of class-mean matrix and $D$. (4) The $i$-th row of the left orthonormal transformation of the product of $L$ linear classifiers aligns with the $i$-th column of the right orthonormal transformation of the product of class-mean matrix and $D$. (5) We provide the estimation of singular values about $\hat Y$. Our numerical experiments support these theoretical findings.

Exploring the Unexplored: Understanding the Impact of Layer Adjustments on Image Classification

This paper investigates how adjustments to deep learning architectures impact model performance in image classification. Small-scale experiments generate initial insights although the trends observed are not consistent with the entire dataset. Filtering operations in the image processing pipeline are crucial, with image filtering before pre-processing yielding better results. The choice and order of layers as well as filter placement significantly impact model performance. This study provides valuable insights into optimizing deep learning models, with potential avenues for future research including collaborative platforms.

On Cooperative Coevolution and Global Crossover

Cooperative coevolutionary algorithms (CCEAs) divide a given problem in to a number of subproblems and use an evolutionary algorithm to solve each subproblem. This short paper is concerned with the scenario under which only a single, global fitness measure exists. By removing the typically used subproblem partnering mechanism, it is suggested that such CCEAs can be viewed as making use of a generalised version of the global crossover operator introduced in early Evolution Strategies. Using the well-known NK model of fitness landscapes, the effects of varying aspects of global crossover with respect to the ruggedness of the underlying fitness landscape are explored. Results suggest improvements over the most widely used form of CCEAs, something further demonstrated using other well-known test functions.

Citation Sentiment Changes Analysis

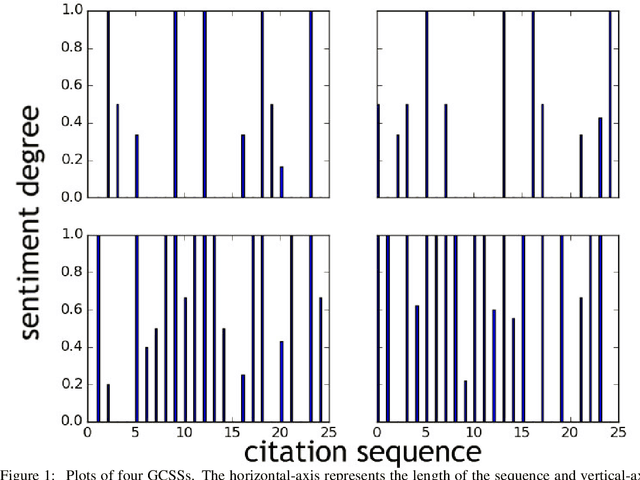
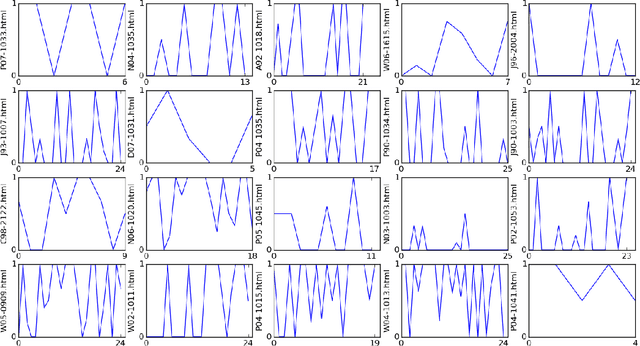
Metrics for measuring the citation sentiment changes were introduced. Citation sentiment changes can be observed from global citation sentiment sequences (GCSSs). With respect to a cited paper, the citation sentiment sequences were analysed across a collection of citing papers ordered by the published time. For analysing GCSSs, Eddy Dissipation Rate (EDR) was adopted, with the hypothesis that the GCSSs pattern differences can be spotted by EDR based method. Preliminary evidence showed that EDR based method holds the potential for analysing a publication's impact in a time series fashion.

Optimize transfer learning for lung diseases in bronchoscopy using a new concept: sequential fine-tuning

Bronchoscopy inspection as a follow-up procedure from the radiological imaging plays a key role in lung disease diagnosis and determining treatment plans for the patients. Doctors needs to make a decision whether to biopsy the patients timely when performing bronchoscopy. However, the doctors also needs to be very selective with biopsies as biopsies may cause uncontrollable bleeding of the lung tissue which is life-threaten. To help doctors to be more selective on biopsies and provide a second opinion on diagnosis, in this work, we propose a computer-aided diagnosis (CAD) system for lung diseases including cancers and tuberculosis (TB). The system is developed based on transfer learning. We propose a novel transfer learning method: sentential fine-tuning . Compared to traditional fine-tuning methods, our methods achieves the best performance. We obtained a overall accuracy of 77.0% a dataset of 81 normal cases, 76 tuberculosis cases and 277 lung cancer cases while the other traditional transfer learning methods achieve an accuracy of 73% and 68%. . The detection accuracy of our method for cancers, TB and normal cases are 87%, 54% and 91% respectively. This indicates that the CAD system has potential to improve lung disease diagnosis accuracy in bronchoscopy and it also might be used to be more selective with biopsies.