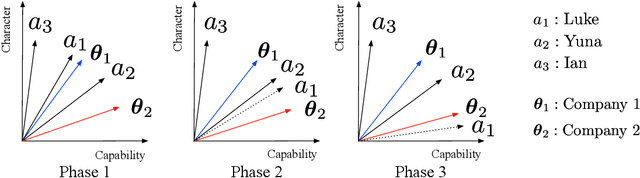
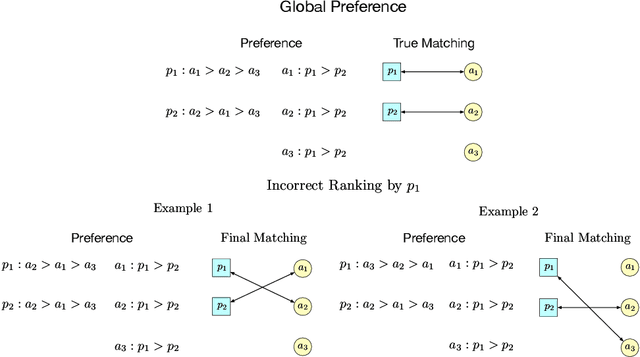
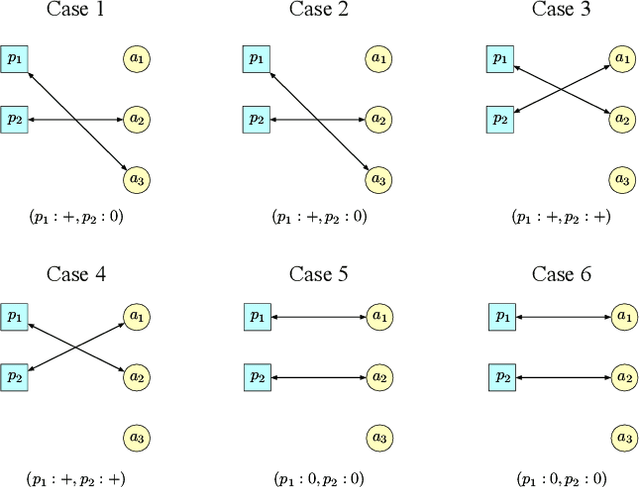
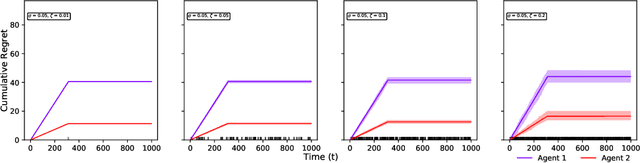
Rate-Optimal Contextual Online Matching Bandit

Two-sided online matching platforms have been employed in various markets. However, agents' preferences in present market are usually implicit and unknown and must be learned from data. With the growing availability of side information involved in the decision process, modern online matching methodology demands the capability to track preference dynamics for agents based on their contextual information. This motivates us to consider a novel Contextual Online Matching Bandit prOblem (COMBO), which allows dynamic preferences in matching decisions. Existing works focus on multi-armed bandit with static preference, but this is insufficient: the two-sided preference changes as along as one-side's contextual information updates, resulting in non-static matching. In this paper, we propose a Centralized Contextual - Explore Then Commit (CC-ETC) algorithm to adapt to the COMBO. CC-ETC solves online matching with dynamic preference. In theory, we show that CC-ETC achieves a sublinear regret upper bound O(log(T)) and is a rate-optimal algorithm by proving a matching lower bound. In the experiments, we demonstrate that CC-ETC is robust to variant preference schemes, dimensions of contexts, reward noise levels, and contexts variation levels.

Federated Online Sparse Decision Making

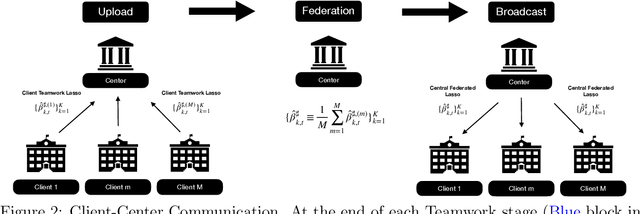
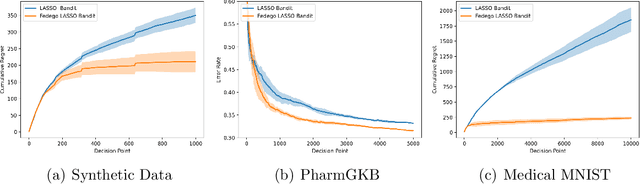
This paper presents a novel federated linear contextual bandits model, where individual clients face different K-armed stochastic bandits with high-dimensional decision context and coupled through common global parameters. By leveraging the sparsity structure of the linear reward , a collaborative algorithm named \texttt{Fedego Lasso} is proposed to cope with the heterogeneity across clients without exchanging local decision context vectors or raw reward data. \texttt{Fedego Lasso} relies on a novel multi-client teamwork-selfish bandit policy design, and achieves near-optimal regrets for shared parameter cases with logarithmic communication costs. In addition, a new conceptual tool called federated-egocentric policies is introduced to delineate exploration-exploitation trade-off. Experiments demonstrate the effectiveness of the proposed algorithms on both synthetic and real-world datasets.

Bayes-Optimal Classifiers under Group Fairness

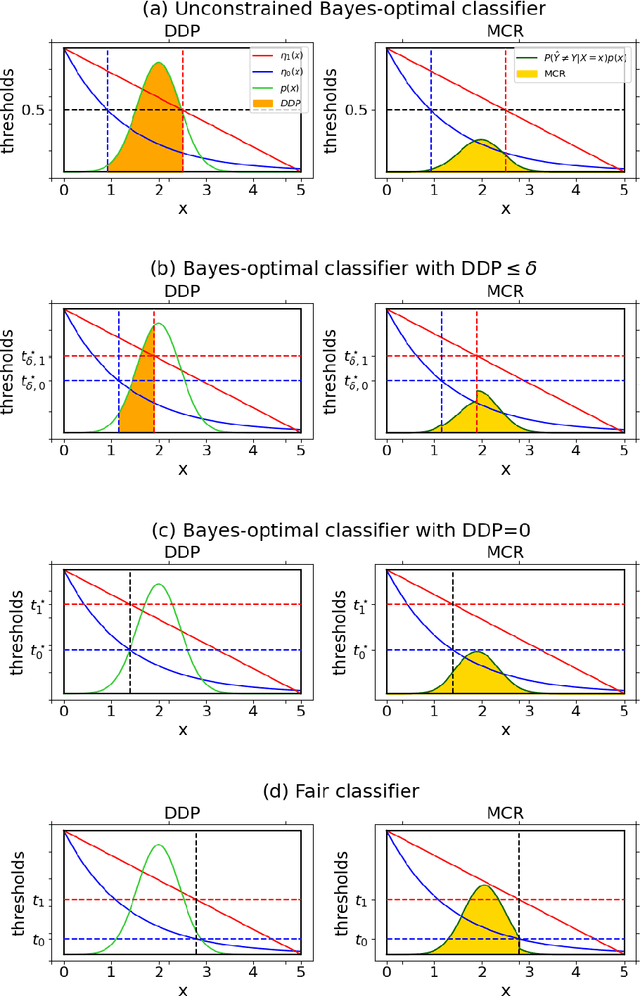
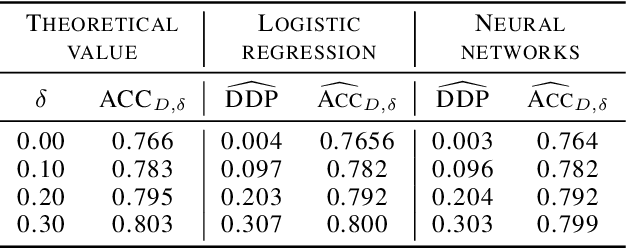
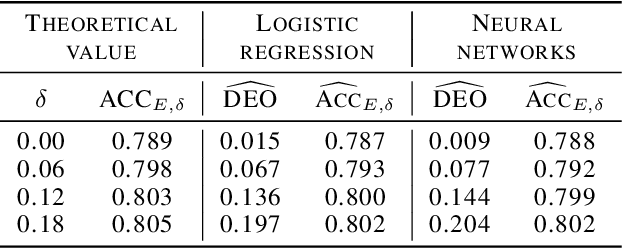
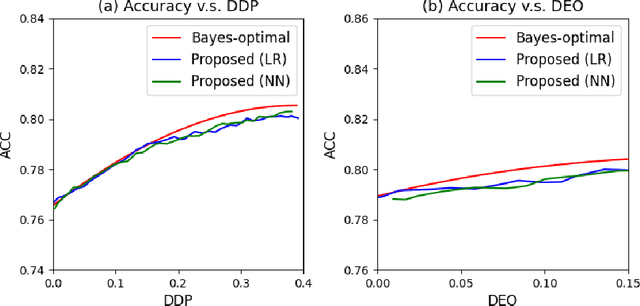
Machine learning algorithms are becoming integrated into more and more high-stakes decision-making processes, such as in social welfare issues. Due to the need of mitigating the potentially disparate impacts from algorithmic predictions, many approaches have been proposed in the emerging area of fair machine learning. However, the fundamental problem of characterizing Bayes-optimal classifiers under various group fairness constraints has only been investigated in some special cases. Based on the classical Neyman-Pearson argument (Neyman and Pearson, 1933; Shao, 2003) for optimal hypothesis testing, this paper provides a unified framework for deriving Bayes-optimal classifiers under group fairness. This enables us to propose a group-based thresholding method that can directly control disparity, and more importantly, achieve an optimal fairness-accuracy tradeoff. These advantages are supported by experiments.

Enhanced Nearest Neighbor Classification for Crowdsourcing

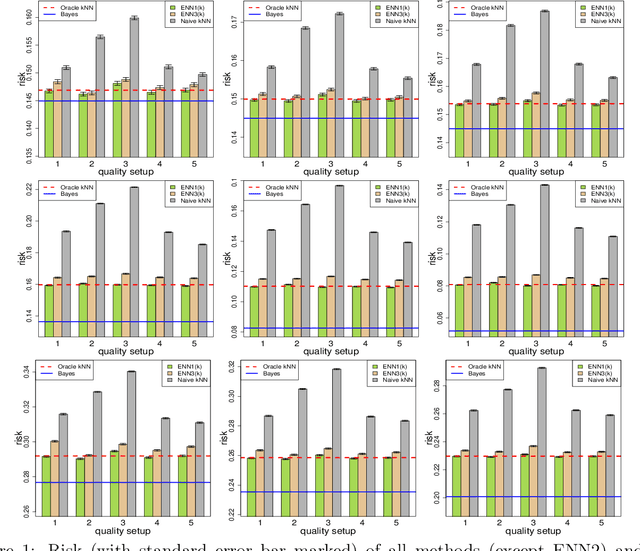
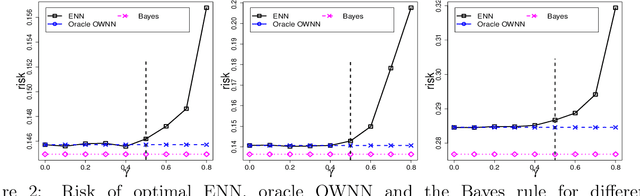
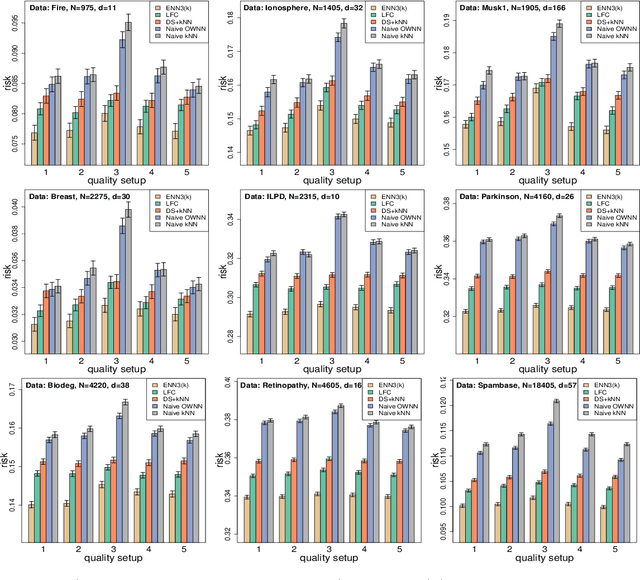
In machine learning, crowdsourcing is an economical way to label a large amount of data. However, the noise in the produced labels may deteriorate the accuracy of any classification method applied to the labelled data. We propose an enhanced nearest neighbor classifier (ENN) to overcome this issue. Two algorithms are developed to estimate the worker quality (which is often unknown in practice): one is to construct the estimate based on the denoised worker labels by applying the $k$NN classifier to the expert data; the other is an iterative algorithm that works even without access to the expert data. Other than strong numerical evidence, our proposed methods are proven to achieve the same regret as its oracle version based on high-quality expert data. As a technical by-product, a lower bound on the sample size assigned to each worker to reach the optimal convergence rate of regret is derived.

Attention Enables Zero Approximation Error

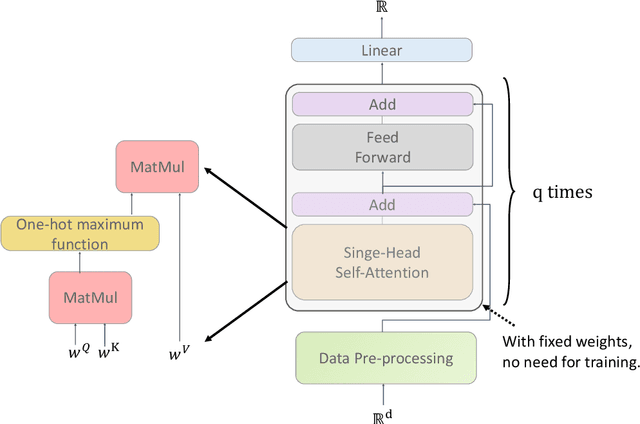
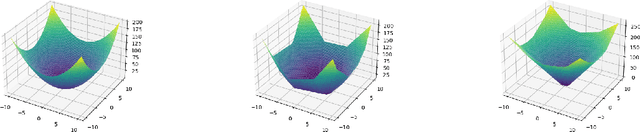
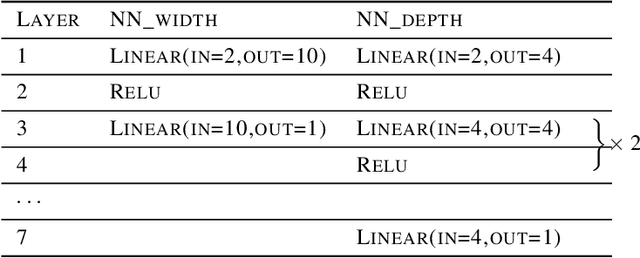
Deep learning models have been widely applied in various aspects of daily life. Many variant models based on deep learning structures have achieved even better performances. Attention-based architectures have become almost ubiquitous in deep learning structures. Especially, the transformer model has now defeated the convolutional neural network in image classification tasks to become the most widely used tool. However, the theoretical properties of attention-based models are seldom considered. In this work, we show that with suitable adaptations, the single-head self-attention transformer with a fixed number of transformer encoder blocks and free parameters is able to generate any desired polynomial of the input with no error. The number of transformer encoder blocks is the same as the degree of the target polynomial. Even more exciting, we find that these transformer encoder blocks in this model do not need to be trained. As a direct consequence, we show that the single-head self-attention transformer with increasing numbers of free parameters is universal. These surprising theoretical results clearly explain the outstanding performances of the transformer model and may shed light on future modifications in real applications. We also provide some experiments to verify our theoretical result.

Optimal Learning Rates of Deep Convolutional Neural Networks: Additive Ridge Functions

Convolutional neural networks have shown extraordinary abilities in many applications, especially those related to the classification tasks. However, for the regression problem, the abilities of convolutional structures have not been fully understood, and further investigation is needed. In this paper, we consider the mean squared error analysis for deep convolutional neural networks. We show that, for additive ridge functions, convolutional neural networks followed by one fully connected layer with ReLU activation functions can reach optimal mini-max rates (up to a log factor). The convergence rates are dimension independent. This work shows the statistical optimality of convolutional neural networks and may shed light on why convolutional neural networks are able to behave well for high dimensional input.

Benefit of Interpolation in Nearest Neighbor Algorithms

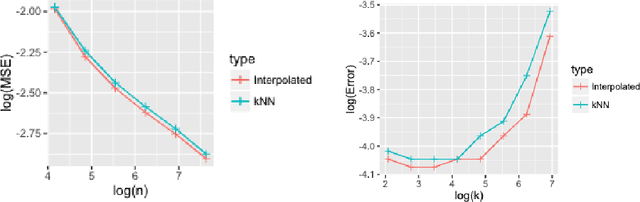
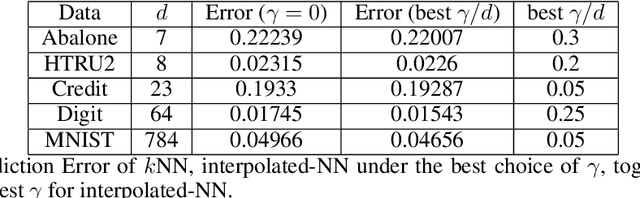
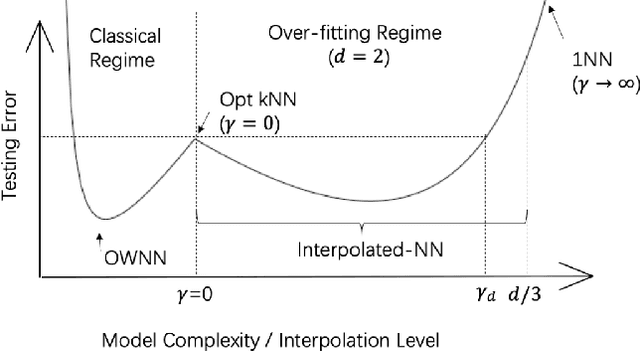
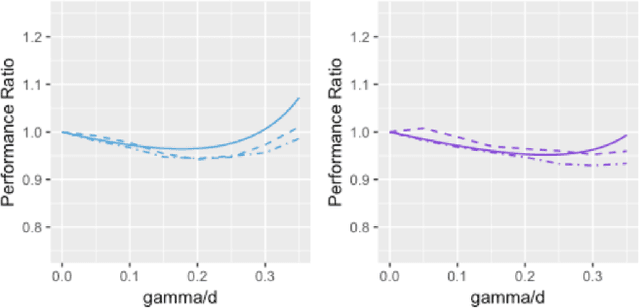
In some studies \citep[e.g.,][]{zhang2016understanding} of deep learning, it is observed that over-parametrized deep neural networks achieve a small testing error even when the training error is almost zero. Despite numerous works towards understanding this so-called "double descent" phenomenon \citep[e.g.,][]{belkin2018reconciling,belkin2019two}, in this paper, we turn into another way to enforce zero training error (without over-parametrization) through a data interpolation mechanism. Specifically, we consider a class of interpolated weighting schemes in the nearest neighbors (NN) algorithms. By carefully characterizing the multiplicative constant in the statistical risk, we reveal a U-shaped performance curve for the level of data interpolation in both classification and regression setups. This sharpens the existing result \citep{belkin2018does} that zero training error does not necessarily jeopardize predictive performances and claims a counter-intuitive result that a mild degree of data interpolation actually {\em strictly} improve the prediction performance and statistical stability over those of the (un-interpolated) $k$-NN algorithm. In the end, the universality of our results, such as change of distance measure and corrupted testing data, will also be discussed.

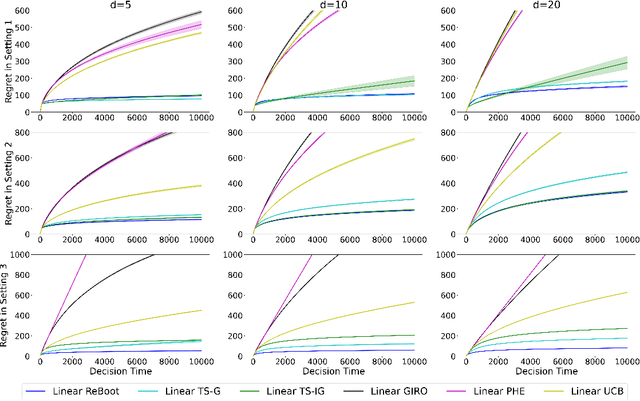
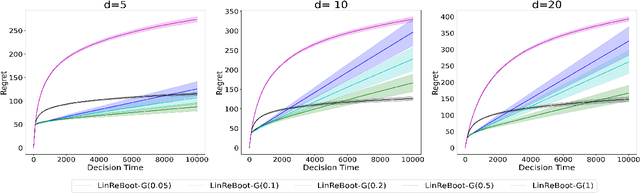
Residual Bootstrap Exploration for Stochastic Linear Bandit

We propose a new bootstrap-based online algorithm for stochastic linear bandit problems. The key idea is to adopt residual bootstrap exploration, in which the agent estimates the next step reward by re-sampling the residuals of mean reward estimate. Our algorithm, residual bootstrap exploration for stochastic linear bandit (\texttt{LinReBoot}), estimates the linear reward from its re-sampling distribution and pulls the arm with the highest reward estimate. In particular, we contribute a theoretical framework to demystify residual bootstrap-based exploration mechanisms in stochastic linear bandit problems. The key insight is that the strength of bootstrap exploration is based on collaborated optimism between the online-learned model and the re-sampling distribution of residuals. Such observation enables us to show that the proposed \texttt{LinReBoot} secure a high-probability $\tilde{O}(d \sqrt{n})$ sub-linear regret under mild conditions. Our experiments support the easy generalizability of the \texttt{ReBoot} principle in the various formulations of linear bandit problems and show the significant computational efficiency of \texttt{LinReBoot}.

Unlabeled Data Help: Minimax Analysis and Adversarial Robustness

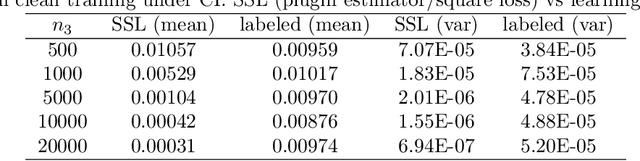
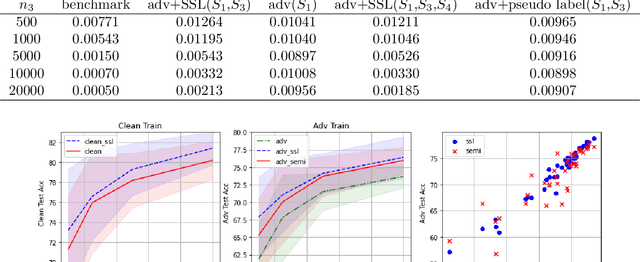
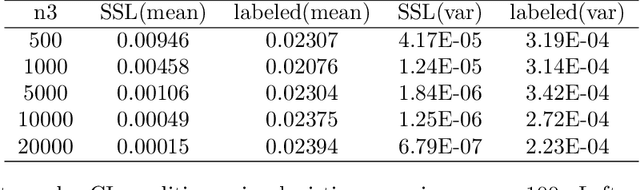
The recent proposed self-supervised learning (SSL) approaches successfully demonstrate the great potential of supplementing learning algorithms with additional unlabeled data. However, it is still unclear whether the existing SSL algorithms can fully utilize the information of both labelled and unlabeled data. This paper gives an affirmative answer for the reconstruction-based SSL algorithm \citep{lee2020predicting} under several statistical models. While existing literature only focuses on establishing the upper bound of the convergence rate, we provide a rigorous minimax analysis, and successfully justify the rate-optimality of the reconstruction-based SSL algorithm under different data generation models. Furthermore, we incorporate the reconstruction-based SSL into the existing adversarial training algorithms and show that learning from unlabeled data helps improve the robustness.

High-Dimensional Inference over Networks: Linear Convergence and Statistical Guarantees

We study sparse linear regression over a network of agents, modeled as an undirected graph and no server node. The estimation of the $s$-sparse parameter is formulated as a constrained LASSO problem wherein each agent owns a subset of the $N$ total observations. We analyze the convergence rate and statistical guarantees of a distributed projected gradient tracking-based algorithm under high-dimensional scaling, allowing the ambient dimension $d$ to grow with (and possibly exceed) the sample size $N$. Our theory shows that, under standard notions of restricted strong convexity and smoothness of the loss functions, suitable conditions on the network connectivity and algorithm tuning, the distributed algorithm converges globally at a {\it linear} rate to an estimate that is within the centralized {\it statistical precision} of the model, $O(s\log d/N)$. When $s\log d/N=o(1)$, a condition necessary for statistical consistency, an $\varepsilon$-optimal solution is attained after $\mathcal{O}(\kappa \log (1/\varepsilon))$ gradient computations and $O (\kappa/(1-\rho) \log (1/\varepsilon))$ communication rounds, where $\kappa$ is the restricted condition number of the loss function and $\rho$ measures the network connectivity. The computation cost matches that of the centralized projected gradient algorithm despite having data distributed; whereas the communication rounds reduce as the network connectivity improves. Overall, our study reveals interesting connections between statistical efficiency, network connectivity \& topology, and convergence rate in high dimensions.