Attention Enables Zero Approximation Error

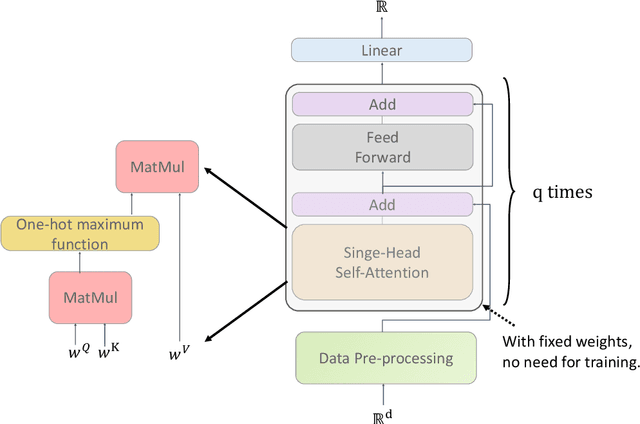
Deep learning models have been widely applied in various aspects of daily life. Many variant models based on deep learning structures have achieved even better performances. Attention-based architectures have become almost ubiquitous in deep learning structures. Especially, the transformer model has now defeated the convolutional neural network in image classification tasks to become the most widely used tool. However, the theoretical properties of attention-based models are seldom considered. In this work, we show that with suitable adaptations, the single-head self-attention transformer with a fixed number of transformer encoder blocks and free parameters is able to generate any desired polynomial of the input with no error. The number of transformer encoder blocks is the same as the degree of the target polynomial. Even more exciting, we find that these transformer encoder blocks in this model do not need to be trained. As a direct consequence, we show that the single-head self-attention transformer with increasing numbers of free parameters is universal. These surprising theoretical results clearly explain the outstanding performances of the transformer model and may shed light on future modifications in real applications. We also provide some experiments to verify our theoretical result.

Optimal Learning Rates of Deep Convolutional Neural Networks: Additive Ridge Functions

Convolutional neural networks have shown extraordinary abilities in many applications, especially those related to the classification tasks. However, for the regression problem, the abilities of convolutional structures have not been fully understood, and further investigation is needed. In this paper, we consider the mean squared error analysis for deep convolutional neural networks. We show that, for additive ridge functions, convolutional neural networks followed by one fully connected layer with ReLU activation functions can reach optimal mini-max rates (up to a log factor). The convergence rates are dimension independent. This work shows the statistical optimality of convolutional neural networks and may shed light on why convolutional neural networks are able to behave well for high dimensional input.

Theory of Deep Convolutional Neural Networks II: Spherical Analysis

Deep learning based on deep neural networks of various structures and architectures has been powerful in many practical applications, but it lacks enough theoretical verifications. In this paper, we consider a family of deep convolutional neural networks applied to approximate functions on the unit sphere $\mathbb{S}^{d-1}$ of $\mathbb{R}^d$. Our analysis presents rates of uniform approximation when the approximated function lies in the Sobolev space $W^r_\infty (\mathbb{S}^{d-1})$ with $r>0$ or takes an additive ridge form. Our work verifies theoretically the modelling and approximation ability of deep convolutional neural networks followed by downsampling and one fully connected layer or two. The key idea of our spherical analysis is to use the inner product form of the reproducing kernels of the spaces of spherical harmonics and then to apply convolutional factorizations of filters to realize the generated linear features.

Towards Understanding the Spectral Bias of Deep Learning

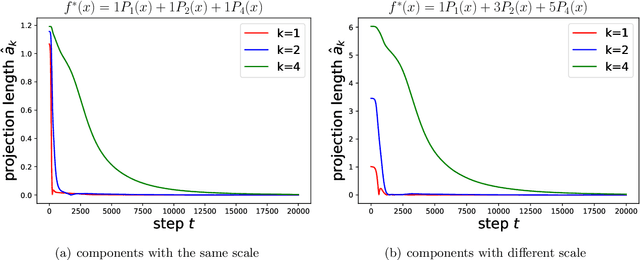
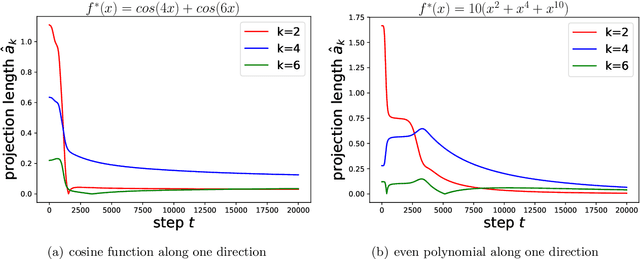
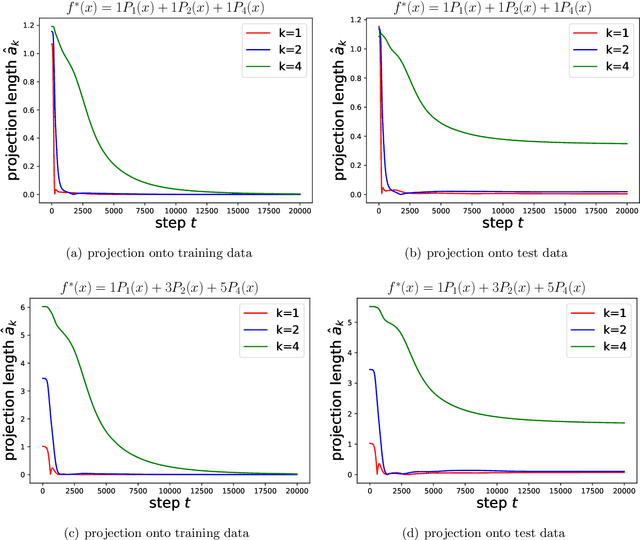
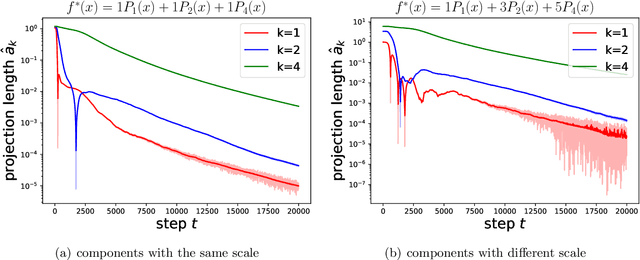
An intriguing phenomenon observed during training neural networks is the spectral bias, where neural networks are biased towards learning less complex functions. The priority of learning functions with low complexity might be at the core of explaining generalization ability of neural network, and certain efforts have been made to provide theoretical explanation for spectral bias. However, there is still no satisfying theoretical result justifying the underlying mechanism of spectral bias. In this paper, we give a comprehensive and rigorous explanation for spectral bias and relate it with the neural tangent kernel function proposed in recent work. We prove that the training process of neural networks can be decomposed along different directions defined by the eigenfunctions of the neural tangent kernel, where each direction has its own convergence rate and the rate is determined by the corresponding eigenvalue. We then provide a case study when the input data is uniformly distributed over the unit sphere, and show that lower degree spherical harmonics are easier to be learned by over-parameterized neural networks.