DEREC-SIMPRO: unlock Language Model benefits to advance Synthesis in Data Clean Room

Data collaboration via Data Clean Room offers value but raises privacy concerns, which can be addressed through synthetic data and multi-table synthesizers. Common multi-table synthesizers fail to perform when subjects occur repeatedly in both tables. This is an urgent yet unresolved problem, since having both tables with repeating subjects is common. To improve performance in this scenario, we present the DEREC 3-step pre-processing pipeline to generalize adaptability of multi-table synthesizers. We also introduce the SIMPRO 3-aspect evaluation metrics, which leverage conditional distribution and large-scale simultaneous hypothesis testing to provide comprehensive feedback on synthetic data fidelity at both column and table levels. Results show that using DEREC improves fidelity, and multi-table synthesizers outperform single-table counterparts in collaboration settings. Together, the DEREC-SIMPRO pipeline offers a robust solution for generalizing data collaboration, promoting a more efficient, data-driven society.

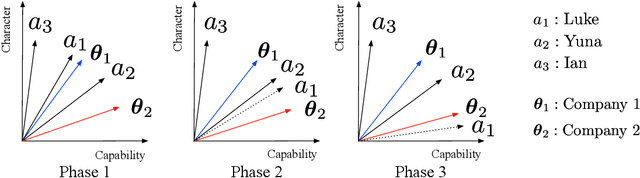
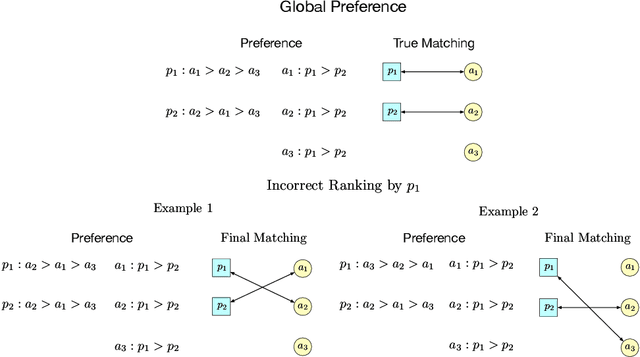
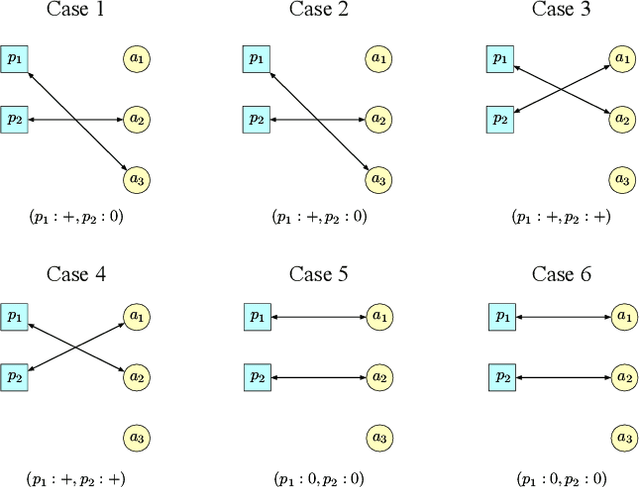
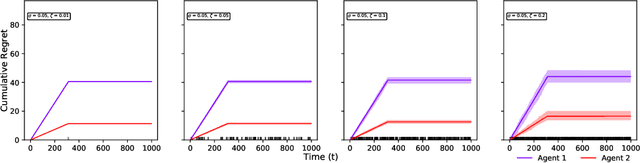
Rate-Optimal Contextual Online Matching Bandit

Two-sided online matching platforms have been employed in various markets. However, agents' preferences in present market are usually implicit and unknown and must be learned from data. With the growing availability of side information involved in the decision process, modern online matching methodology demands the capability to track preference dynamics for agents based on their contextual information. This motivates us to consider a novel Contextual Online Matching Bandit prOblem (COMBO), which allows dynamic preferences in matching decisions. Existing works focus on multi-armed bandit with static preference, but this is insufficient: the two-sided preference changes as along as one-side's contextual information updates, resulting in non-static matching. In this paper, we propose a Centralized Contextual - Explore Then Commit (CC-ETC) algorithm to adapt to the COMBO. CC-ETC solves online matching with dynamic preference. In theory, we show that CC-ETC achieves a sublinear regret upper bound O(log(T)) and is a rate-optimal algorithm by proving a matching lower bound. In the experiments, we demonstrate that CC-ETC is robust to variant preference schemes, dimensions of contexts, reward noise levels, and contexts variation levels.

Online Forgetting Process for Linear Regression Models

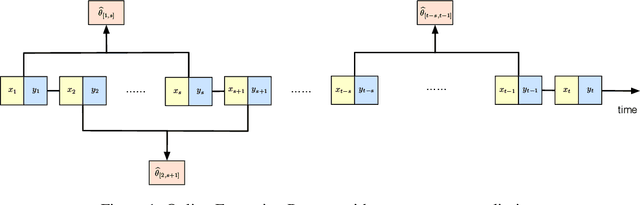
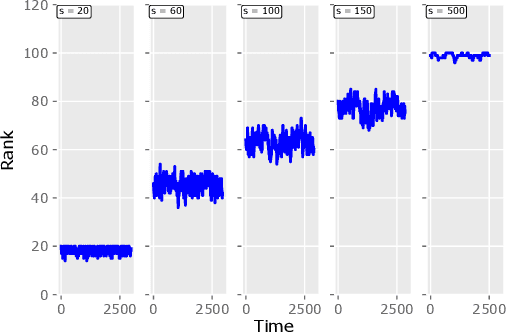
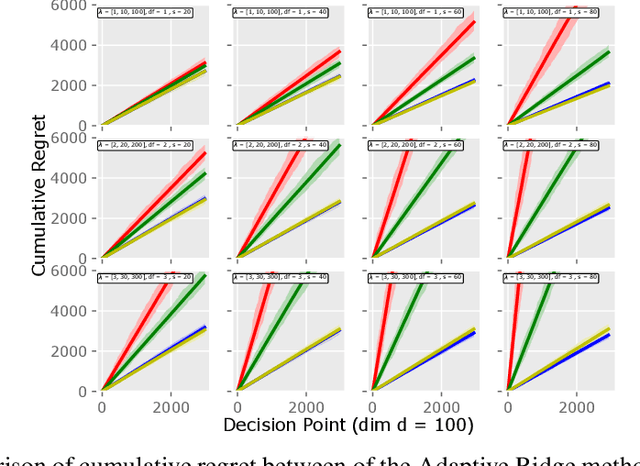
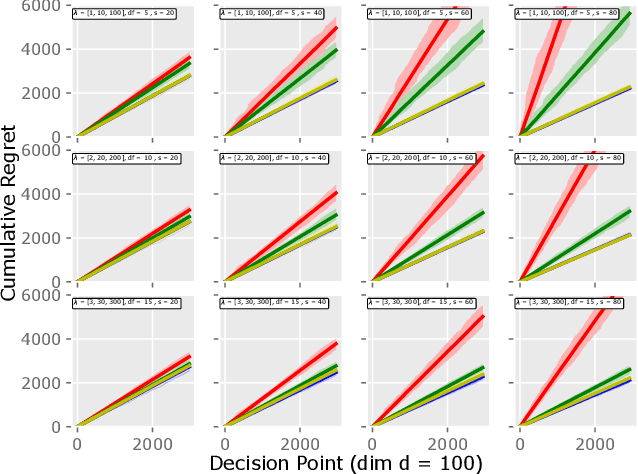
Motivated by the EU's "Right To Be Forgotten" regulation, we initiate a study of statistical data deletion problems where users' data are accessible only for a limited period of time. This setting is formulated as an online supervised learning task with \textit{constant memory limit}. We propose a deletion-aware algorithm \texttt{FIFD-OLS} for the low dimensional case, and witness a catastrophic rank swinging phenomenon due to the data deletion operation, which leads to statistical inefficiency. As a remedy, we propose the \texttt{FIFD-Adaptive Ridge} algorithm with a novel online regularization scheme, that effectively offsets the uncertainty from deletion. In theory, we provide the cumulative regret upper bound for both online forgetting algorithms. In the experiment, we showed \texttt{FIFD-Adaptive Ridge} outperforms the ridge regression algorithm with fixed regularization level, and hopefully sheds some light on more complex statistical models.