George J. Pappas
Variational Autoencoding Neural Operators
Feb 20, 2023Abstract:Unsupervised learning with functional data is an emerging paradigm of machine learning research with applications to computer vision, climate modeling and physical systems. A natural way of modeling functional data is by learning operators between infinite dimensional spaces, leading to discretization invariant representations that scale independently of the sample grid resolution. Here we present Variational Autoencoding Neural Operators (VANO), a general strategy for making a large class of operator learning architectures act as variational autoencoders. For this purpose, we provide a novel rigorous mathematical formulation of the variational objective in function spaces for training. VANO first maps an input function to a distribution over a latent space using a parametric encoder and then decodes a sample from the latent distribution to reconstruct the input, as in classic variational autoencoders. We test VANO with different model set-ups and architecture choices for a variety of benchmarks. We start from a simple Gaussian random field where we can analytically track what the model learns and progressively transition to more challenging benchmarks including modeling phase separation in Cahn-Hilliard systems and real world satellite data for measuring Earth surface deformation.
Federated Temporal Difference Learning with Linear Function Approximation under Environmental Heterogeneity
Feb 04, 2023


Abstract:We initiate the study of federated reinforcement learning under environmental heterogeneity by considering a policy evaluation problem. Our setup involves $N$ agents interacting with environments that share the same state and action space but differ in their reward functions and state transition kernels. Assuming agents can communicate via a central server, we ask: Does exchanging information expedite the process of evaluating a common policy? To answer this question, we provide the first comprehensive finite-time analysis of a federated temporal difference (TD) learning algorithm with linear function approximation, while accounting for Markovian sampling, heterogeneity in the agents' environments, and multiple local updates to save communication. Our analysis crucially relies on several novel ingredients: (i) deriving perturbation bounds on TD fixed points as a function of the heterogeneity in the agents' underlying Markov decision processes (MDPs); (ii) introducing a virtual MDP to closely approximate the dynamics of the federated TD algorithm; and (iii) using the virtual MDP to make explicit connections to federated optimization. Putting these pieces together, we rigorously prove that in a low-heterogeneity regime, exchanging model estimates leads to linear convergence speedups in the number of agents.
Certified Invertibility in Neural Networks via Mixed-Integer Programming
Jan 27, 2023Abstract:Neural networks are notoriously vulnerable to adversarial attacks -- small imperceptible perturbations that can change the network's output drastically. In the reverse direction, there may exist large, meaningful perturbations that leave the network's decision unchanged (excessive invariance, nonivertibility). We study the latter phenomenon in two contexts: (a) discrete-time dynamical system identification, as well as (b) calibration of the output of one neural network to the output of another (neural network matching). For ReLU networks and $L_p$ norms ($p=1,2,\infty$), we formulate these optimization problems as mixed-integer programs (MIPs) that apply to neural network approximators of dynamical systems. We also discuss the applicability of our results to invertibility certification in transformations between neural networks (e.g. at different levels of pruning).
Temporal Difference Learning with Compressed Updates: Error-Feedback meets Reinforcement Learning
Jan 03, 2023Abstract:In large-scale machine learning, recent works have studied the effects of compressing gradients in stochastic optimization in order to alleviate the communication bottleneck. These works have collectively revealed that stochastic gradient descent (SGD) is robust to structured perturbations such as quantization, sparsification, and delays. Perhaps surprisingly, despite the surge of interest in large-scale, multi-agent reinforcement learning, almost nothing is known about the analogous question: Are common reinforcement learning (RL) algorithms also robust to similar perturbations? In this paper, we investigate this question by studying a variant of the classical temporal difference (TD) learning algorithm with a perturbed update direction, where a general compression operator is used to model the perturbation. Our main technical contribution is to show that compressed TD algorithms, coupled with an error-feedback mechanism used widely in optimization, exhibit the same non-asymptotic theoretical guarantees as their SGD counterparts. We then extend our results significantly to nonlinear stochastic approximation algorithms and multi-agent settings. In particular, we prove that for multi-agent TD learning, one can achieve linear convergence speedups in the number of agents while communicating just $\tilde{O}(1)$ bits per agent at each time step. Our work is the first to provide finite-time results in RL that account for general compression operators and error-feedback in tandem with linear function approximation and Markovian sampling. Our analysis hinges on studying the drift of a novel Lyapunov function that captures the dynamics of a memory variable introduced by error feedback.
Adaptive Conformal Prediction for Motion Planning among Dynamic Agents
Dec 01, 2022Abstract:This paper proposes an algorithm for motion planning among dynamic agents using adaptive conformal prediction. We consider a deterministic control system and use trajectory predictors to predict the dynamic agents' future motion, which is assumed to follow an unknown distribution. We then leverage ideas from adaptive conformal prediction to dynamically quantify prediction uncertainty from an online data stream. Particularly, we provide an online algorithm uses delayed agent observations to obtain uncertainty sets for multistep-ahead predictions with probabilistic coverage. These uncertainty sets are used within a model predictive controller to safely navigate among dynamic agents. While most existing data-driven prediction approached quantify prediction uncertainty heuristically, we quantify the true prediction uncertainty in a distribution-free, adaptive manner that even allows to capture changes in prediction quality and the agents' motion. We empirically evaluate of our algorithm on a simulation case studies where a drone avoids a flying frisbee.
Conformal Prediction for STL Runtime Verification
Nov 03, 2022



Abstract:We are interested in predicting failures of cyber-physical systems during their operation. Particularly, we consider stochastic systems and signal temporal logic specifications, and we want to calculate the probability that the current system trajectory violates the specification. The paper presents two predictive runtime verification algorithms that predict future system states from the current observed system trajectory. As these predictions may not be accurate, we construct prediction regions that quantify prediction uncertainty by using conformal prediction, a statistical tool for uncertainty quantification. Our first algorithm directly constructs a prediction region for the satisfaction measure of the specification so that we can predict specification violations with a desired confidence. The second algorithm constructs prediction regions for future system states first, and uses these to obtain a prediction region for the satisfaction measure. To the best of our knowledge, these are the first formal guarantees for a predictive runtime verification algorithm that applies to widely used trajectory predictors such as RNNs and LSTMs, while being computationally simple and making no assumptions on the underlying distribution. We present numerical experiments of an F-16 aircraft and a self-driving car.
Safe Planning in Dynamic Environments using Conformal Prediction
Oct 19, 2022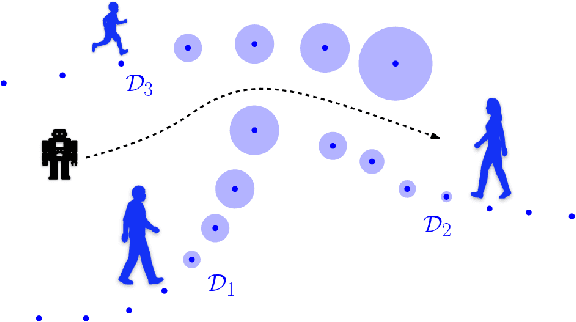
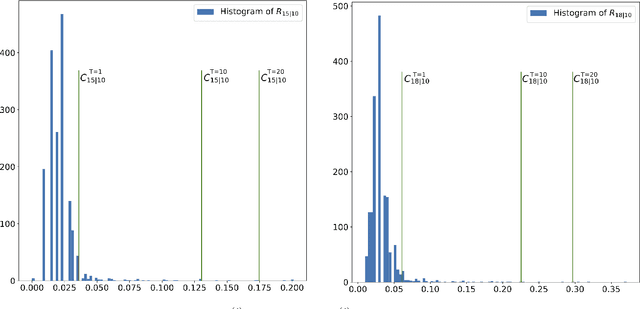
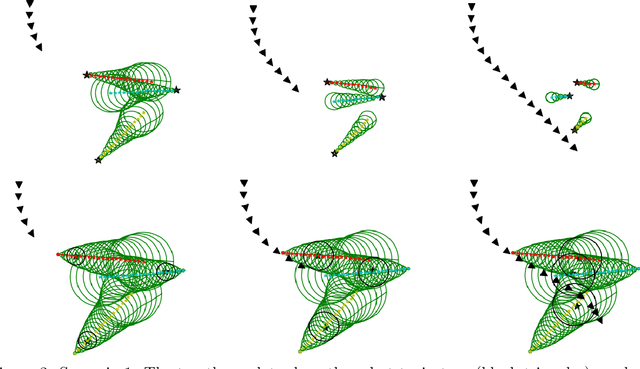

Abstract:We propose a framework for planning in unknown dynamic environments with probabilistic safety guarantees using conformal prediction. Particularly, we design a model predictive controller (MPC) that uses i) trajectory predictions of the dynamic environment, and ii) prediction regions quantifying the uncertainty of the predictions. To obtain prediction regions, we use conformal prediction, a statistical tool for uncertainty quantification, that requires availability of offline trajectory data - a reasonable assumption in many applications such as autonomous driving. The prediction regions are valid, i.e., they hold with a user-defined probability, so that the MPC is provably safe. We illustrate the results in the self-driving car simulator CARLA at a pedestrian-filled intersection. The strength of our approach is compatibility with state of the art trajectory predictors, e.g., RNNs and LSTMs, while making no assumptions on the underlying trajectory-generating distribution. To the best of our knowledge, these are the first results that provide valid safety guarantees in such a setting.
Graph Neural Networks for Multi-Robot Active Information Acquisition
Sep 24, 2022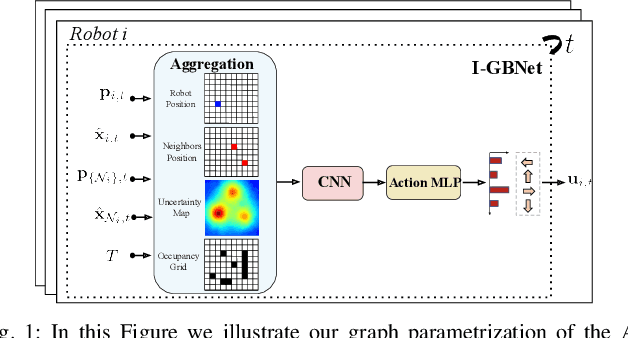
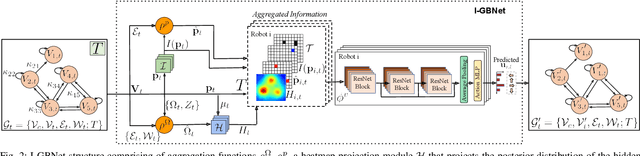
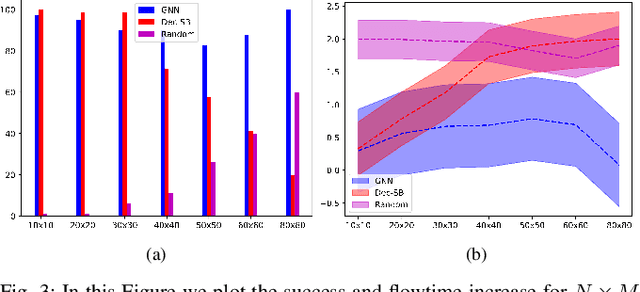
Abstract:This paper addresses the Multi-Robot Active Information Acquisition (AIA) problem, where a team of mobile robots, communicating through an underlying graph, estimates a hidden state expressing a phenomenon of interest. Applications like target tracking, coverage and SLAM can be expressed in this framework. Existing approaches, though, are either not scalable, unable to handle dynamic phenomena or not robust to changes in the communication graph. To counter these shortcomings, we propose an Information-aware Graph Block Network (I-GBNet), an AIA adaptation of Graph Neural Networks, that aggregates information over the graph representation and provides sequential-decision making in a distributed manner. The I-GBNet, trained via imitation learning with a centralized sampling-based expert solver, exhibits permutation equivariance and time invariance, while harnessing the superior scalability, robustness and generalizability to previously unseen environments and robot configurations. Experiments on significantly larger graphs and dimensionality of the hidden state and more complex environments than those seen in training validate the properties of the proposed architecture and its efficacy in the application of localization and tracking of dynamic targets.
Multi-robot Mission Planning in Dynamic Semantic Environments
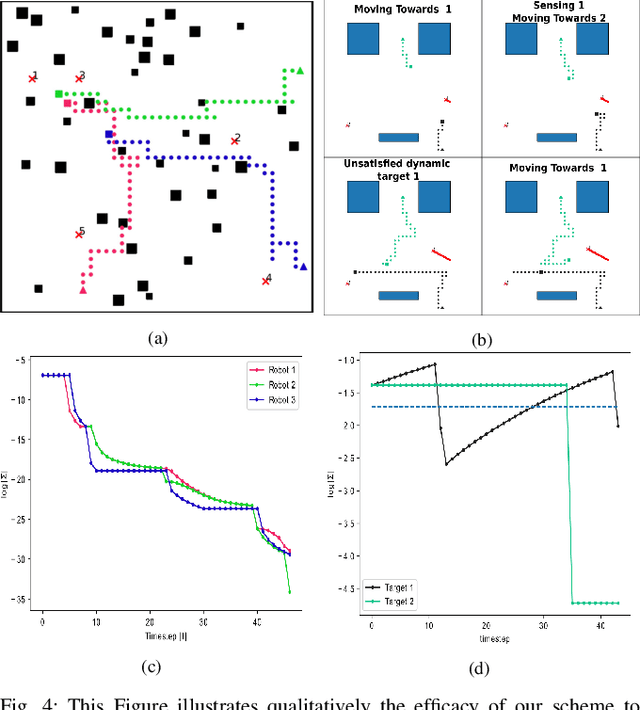
Sep 13, 2022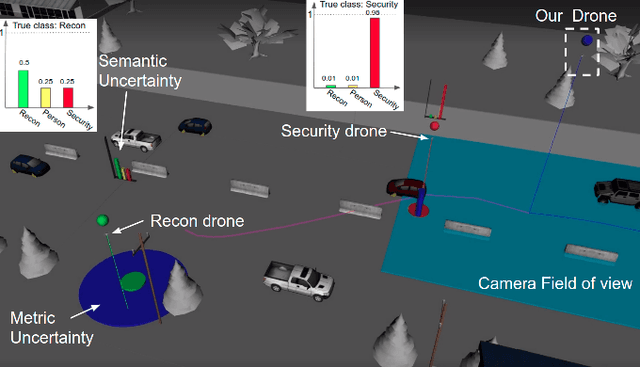
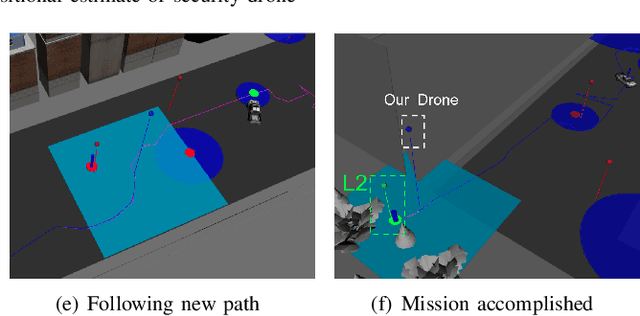
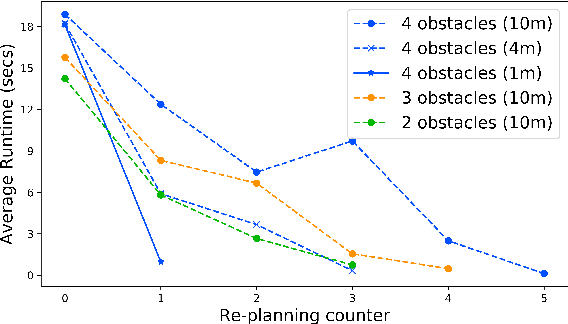
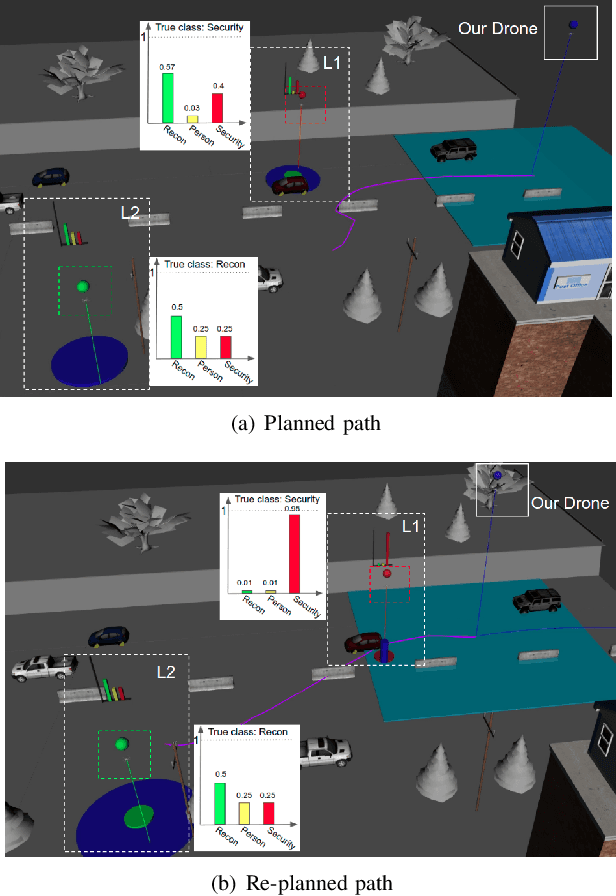
Abstract:This paper addresses a new semantic multi-robot planning problem in uncertain and dynamic environments. Particularly, the environment is occupied with non-cooperative, mobile, uncertain labeled targets. These targets are governed by stochastic dynamics while their current and future positions as well as their semantic labels are uncertain. Our goal is to control mobile sensing robots so that they can accomplish collaborative semantic tasks defined over the uncertain current/future positions and labels of these targets. We express these tasks using Linear Temporal Logic (LTL). We propose a sampling-based approach that explores the robot motion space, the mission specification space, as well as the future configurations of the labeled targets to design optimal paths. These paths are revised online to adapt to uncertain perceptual feedback. To the best of our knowledge, this is the first work that addresses semantic mission planning problems in uncertain and dynamic semantic environments. We provide extensive experiments that demonstrate the efficiency of the proposed method
Statistical Learning Theory for Control: A Finite Sample Perspective
Sep 12, 2022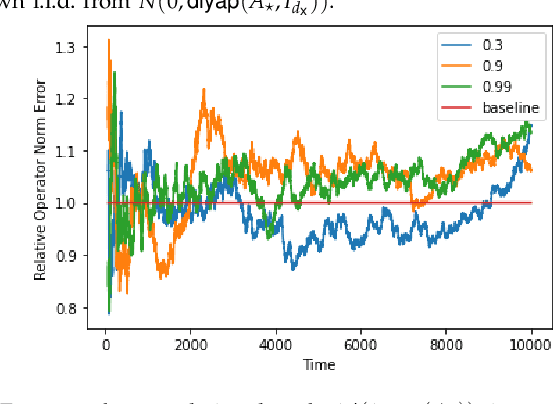
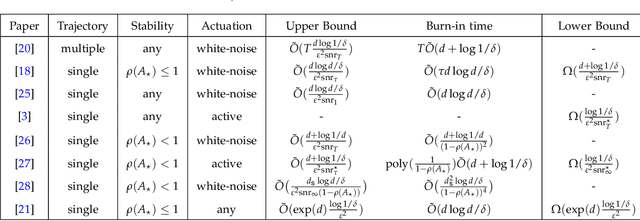
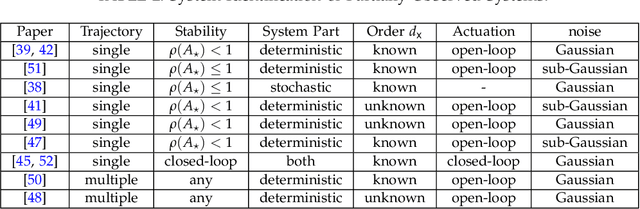

Abstract:This tutorial survey provides an overview of recent non-asymptotic advances in statistical learning theory as relevant to control and system identification. While there has been substantial progress across all areas of control, the theory is most well-developed when it comes to linear system identification and learning for the linear quadratic regulator, which are the focus of this manuscript. From a theoretical perspective, much of the labor underlying these advances has been in adapting tools from modern high-dimensional statistics and learning theory. While highly relevant to control theorists interested in integrating tools from machine learning, the foundational material has not always been easily accessible. To remedy this, we provide a self-contained presentation of the relevant material, outlining all the key ideas and the technical machinery that underpin recent results. We also present a number of open problems and future directions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge