Tipping Points of Evolving Epidemiological Networks: Machine Learning-Assisted, Data-Driven Effective Modeling

We study the tipping point collective dynamics of an adaptive susceptible-infected-susceptible (SIS) epidemiological network in a data-driven, machine learning-assisted manner. We identify a parameter-dependent effective stochastic differential equation (eSDE) in terms of physically meaningful coarse mean-field variables through a deep-learning ResNet architecture inspired by numerical stochastic integrators. We construct an approximate effective bifurcation diagram based on the identified drift term of the eSDE and contrast it with the mean-field SIS model bifurcation diagram. We observe a subcritical Hopf bifurcation in the evolving network's effective SIS dynamics, that causes the tipping point behavior; this takes the form of large amplitude collective oscillations that spontaneously -- yet rarely -- arise from the neighborhood of a (noisy) stationary state. We study the statistics of these rare events both through repeated brute force simulations and by using established mathematical/computational tools exploiting the right-hand-side of the identified SDE. We demonstrate that such a collective SDE can also be identified (and the rare events computations also performed) in terms of data-driven coarse observables, obtained here via manifold learning techniques, in particular Diffusion Maps. The workflow of our study is straightforwardly applicable to other complex dynamics problems exhibiting tipping point dynamics.

Tasks Makyth Models: Machine Learning Assisted Surrogates for Tipping Points

We present a machine learning (ML)-assisted framework bridging manifold learning, neural networks, Gaussian processes, and Equation-Free multiscale modeling, for (a) detecting tipping points in the emergent behavior of complex systems, and (b) characterizing probabilities of rare events (here, catastrophic shifts) near them. Our illustrative example is an event-driven, stochastic agent-based model (ABM) describing the mimetic behavior of traders in a simple financial market. Given high-dimensional spatiotemporal data -- generated by the stochastic ABM -- we construct reduced-order models for the emergent dynamics at different scales: (a) mesoscopic Integro-Partial Differential Equations (IPDEs); and (b) mean-field-type Stochastic Differential Equations (SDEs) embedded in a low-dimensional latent space, targeted to the neighborhood of the tipping point. We contrast the uses of the different models and the effort involved in learning them.

Data-driven and Physics Informed Modelling of Chinese Hamster Ovary Cell Bioreactors

Fed-batch culture is an established operation mode for the production of biologics using mammalian cell cultures. Quantitative modeling integrates both kinetics for some key reaction steps and optimization-driven metabolic flux allocation, using flux balance analysis; this is known to lead to certain mathematical inconsistencies. Here, we propose a physically-informed data-driven hybrid model (a "gray box") to learn models of the dynamical evolution of Chinese Hamster Ovary (CHO) cell bioreactors from process data. The approach incorporates physical laws (e.g. mass balances) as well as kinetic expressions for metabolic fluxes. Machine learning (ML) is then used to (a) directly learn evolution equations (black-box modelling); (b) recover unknown physical parameters ("white-box" parameter fitting) or -- importantly -- (c) learn partially unknown kinetic expressions (gray-box modelling). We encode the convex optimization step of the overdetermined metabolic biophysical system as a differentiable, feed-forward layer into our architectures, connecting partial physical knowledge with data-driven machine learning.

Some of the variables, some of the parameters, some of the times, with some physics known: Identification with partial information

Experimental data is often comprised of variables measured independently, at different sampling rates (non-uniform ${\Delta}$t between successive measurements); and at a specific time point only a subset of all variables may be sampled. Approaches to identifying dynamical systems from such data typically use interpolation, imputation or subsampling to reorganize or modify the training data $\textit{prior}$ to learning. Partial physical knowledge may also be available $\textit{a priori}$ (accurately or approximately), and data-driven techniques can complement this knowledge. Here we exploit neural network architectures based on numerical integration methods and $\textit{a priori}$ physical knowledge to identify the right-hand side of the underlying governing differential equations. Iterates of such neural-network models allow for learning from data sampled at arbitrary time points $\textit{without}$ data modification. Importantly, we integrate the network with available partial physical knowledge in "physics informed gray-boxes"; this enables learning unknown kinetic rates or microbial growth functions while simultaneously estimating experimental parameters.

Certified Invertibility in Neural Networks via Mixed-Integer Programming

Neural networks are notoriously vulnerable to adversarial attacks -- small imperceptible perturbations that can change the network's output drastically. In the reverse direction, there may exist large, meaningful perturbations that leave the network's decision unchanged (excessive invariance, nonivertibility). We study the latter phenomenon in two contexts: (a) discrete-time dynamical system identification, as well as (b) calibration of the output of one neural network to the output of another (neural network matching). For ReLU networks and $L_p$ norms ($p=1,2,\infty$), we formulate these optimization problems as mixed-integer programs (MIPs) that apply to neural network approximators of dynamical systems. We also discuss the applicability of our results to invertibility certification in transformations between neural networks (e.g. at different levels of pruning).

Initializing LSTM internal states via manifold learning

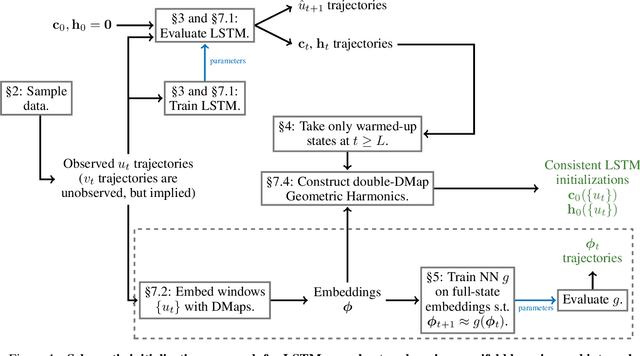
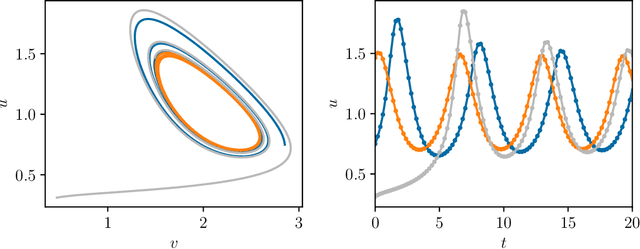
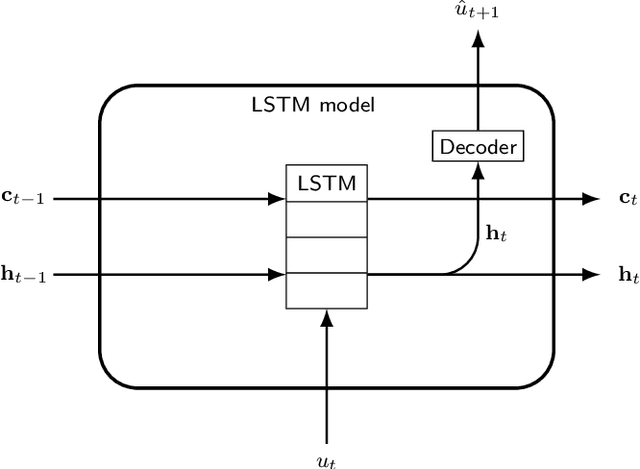
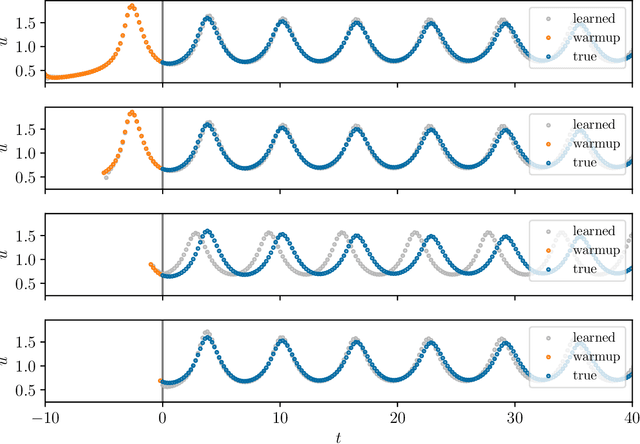
We present an approach, based on learning an intrinsic data manifold, for the initialization of the internal state values of LSTM recurrent neural networks, ensuring consistency with the initial observed input data. Exploiting the generalized synchronization concept, we argue that the converged, "mature" internal states constitute a function on this learned manifold. The dimension of this manifold then dictates the length of observed input time series data required for consistent initialization. We illustrate our approach through a partially observed chemical model system, where initializing the internal LSTM states in this fashion yields visibly improved performance. Finally, we show that learning this data manifold enables the transformation of partially observed dynamics into fully observed ones, facilitating alternative identification paths for nonlinear dynamical systems.