Fast & Robust Image Interpolation using Gradient Graph Laplacian Regularizer

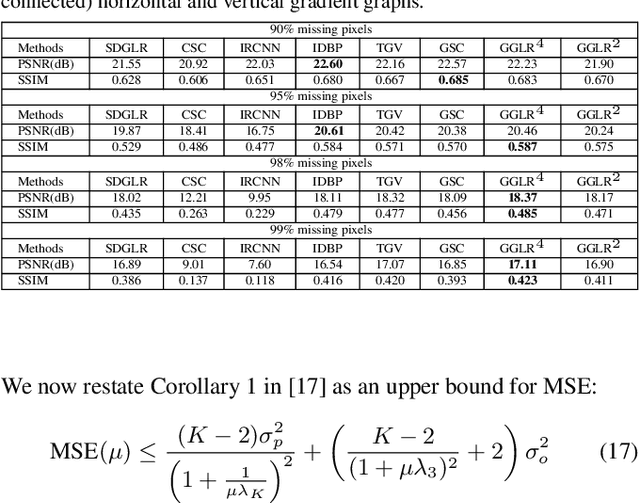
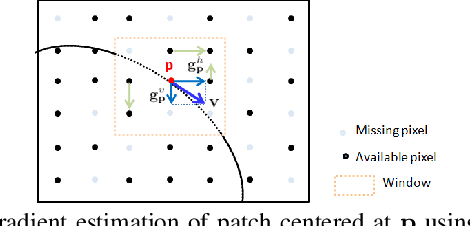
In the graph signal processing (GSP) literature, it has been shown that signal-dependent graph Laplacian regularizer (GLR) can efficiently promote piecewise constant (PWC) signal reconstruction for various image restoration tasks. However, for planar image patches, like total variation (TV), GLR may suffer from the well-known "staircase" effect. To remedy this problem, we generalize GLR to gradient graph Laplacian regularizer (GGLR) that provably promotes piecewise planar (PWP) signal reconstruction for the image interpolation problem -- a 2D grid with randomly missing pixels that requires completion. Specifically, we first construct two higher-order gradient graphs to connect local horizontal and vertical gradients. Each local gradient is estimated using structure tensor, which is robust using known pixels in a small neighborhood, mitigating the problem of larger noise variance when computing gradient of gradients. Moreover, unlike total generalized variation (TGV), GGLR retains the quadratic form of GLR, leading to an unconstrained quadratic programming (QP) problem per iteration that can be solved quickly using conjugate gradient (CG). We derive the means-square-error minimizing weight parameter for GGLR, trading off bias and variance of the signal estimate. Experiments show that GGLR outperformed competing schemes in interpolation quality for severely damaged images at a reduced complexity.

Learning Sparse Graph Laplacian with $K$ Eigenvector Prior via Iterative GLASSO and Projection

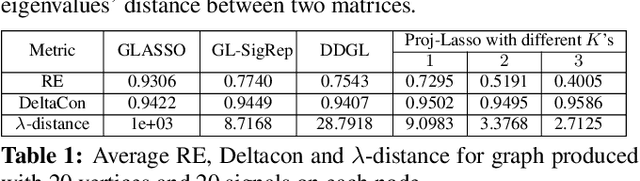
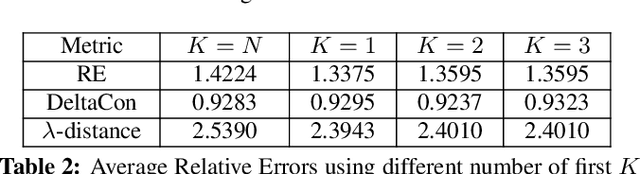
Learning a suitable graph is an important precursor to many graph signal processing (GSP) pipelines, such as graph spectral signal compression and denoising. Previous graph learning algorithms either i) make some assumptions on connectivity (e.g., graph sparsity), or ii) make simple graph edge assumptions such as positive edges only. In this paper, given an empirical covariance matrix $\bar{C}$ computed from data as input, we consider a structural assumption on the graph Laplacian matrix $L$: the first $K$ eigenvectors of $L$ are pre-selected, e.g., based on domain-specific criteria, such as computation requirement, and the remaining eigenvectors are then learned from data. One example use case is image coding, where the first eigenvector is pre-chosen to be constant, regardless of available observed data. We first prove that the subspace of symmetric positive semi-definite (PSD) matrices $H_{u}^+$ with the first $K$ eigenvectors being $\{u_k\}$ in a defined Hilbert space is a convex cone. We then construct an operator to project a given positive definite (PD) matrix $L$ to $H_{u}^+$, inspired by the Gram-Schmidt procedure. Finally, we design an efficient hybrid graphical lasso/projection algorithm to compute the most suitable graph Laplacian matrix $L^* \in H_{u}^+$ given $\bar{C}$. Experimental results show that given the first $K$ eigenvectors as a prior, our algorithm outperforms competing graph learning schemes using a variety of graph comparison metrics.

Unrolling of Deep Graph Total Variation for Image Denoising

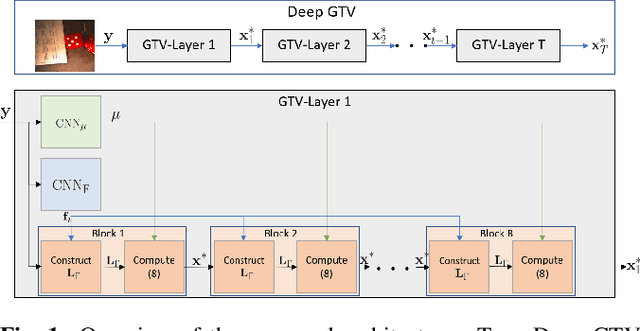
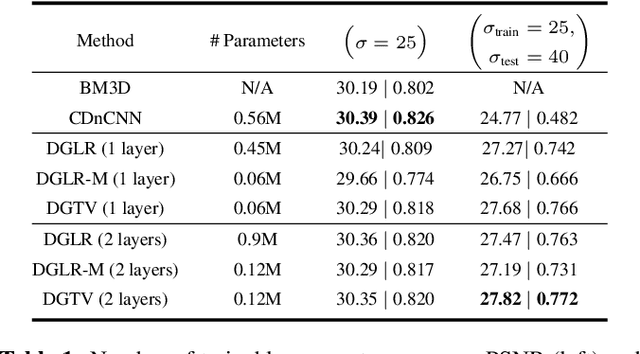
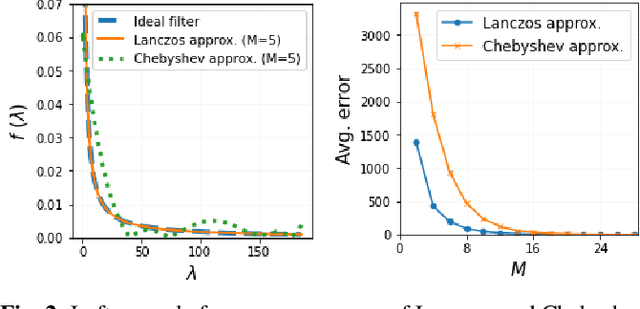
While deep learning (DL) architectures like convolutional neural networks (CNNs) have enabled effective solutions in image denoising, in general their implementations overly rely on training data, lack interpretability, and require tuning of a large parameter set. In this paper, we combine classical graph signal filtering with deep feature learning into a competitive hybrid design---one that utilizes interpretable analytical low-pass graph filters and employs 80% fewer network parameters than state-of-the-art DL denoising scheme DnCNN. Specifically, to construct a suitable similarity graph for graph spectral filtering, we first adopt a CNN to learn feature representations per pixel, and then compute feature distances to establish edge weights. Given a constructed graph, we next formulate a convex optimization problem for denoising using a graph total variation (GTV) prior. Via a $l_1$ graph Laplacian reformulation, we interpret its solution in an iterative procedure as a graph low-pass filter and derive its frequency response. For fast filter implementation, we realize this response using a Lanczos approximation. Experimental results show that in the case of statistical mistmatch, our algorithm outperformed DnCNN by up to 3dB in PSNR.

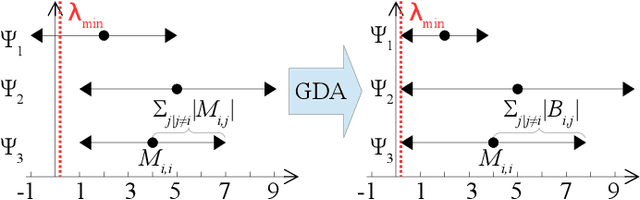
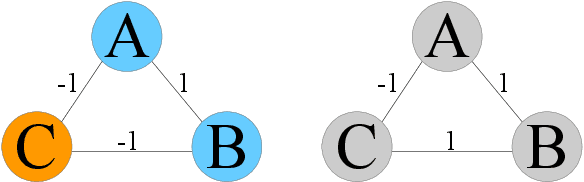
Signed Graph Metric Learning via Gershgorin Disc Alignment

Given a convex and differentiable objective $Q(\M)$ for a real, symmetric matrix $\M$ in the positive definite (PD) cone---used to compute Mahalanobis distances---we propose a fast general metric learning framework that is entirely projection-free. We first assume that $\M$ resides in a space $\cS$ of generalized graph Laplacian matrices (graph metric matrices) corresponding to balanced signed graphs. Unlike low-rank metric matrices common in the literature, $\cS$ includes the important diagonal-only matrices as a special case. The key theorem to circumvent full eigen-decomposition and enable fast metric matrix optimization is Gershgorin disc alignment (GDA): given graph metric matrix $\M \in \cS$ and diagonal matrix $\S$, where $S_{ii} = 1/v_i$ and $\v$ is the first eigenvector of $\M$, we prove that Gershgorin disc left-ends of similar transform $\B = \S \M \S^{-1}$ are perfectly aligned at the smallest eigenvalue $\lambda_{\min}$. Using this theorem, we replace the PD cone constraint in the metric learning problem with tightest possible linear constraints per iteration, so that the alternating optimization of the diagonal / off-diagonal terms in $\M$ can be solved efficiently as linear programs via Frank-Wolfe iterations. We update $\v$ using Locally Optimal Block Preconditioned Conjugate Gradient (LOBPCG) with warm start as matrix entries in $\M$ are optimized successively. Experiments show that our graph metric optimization is significantly faster than cone-projection methods, and produces competitive binary classification performance.

Sampling on Graphs: From Theory to Applications

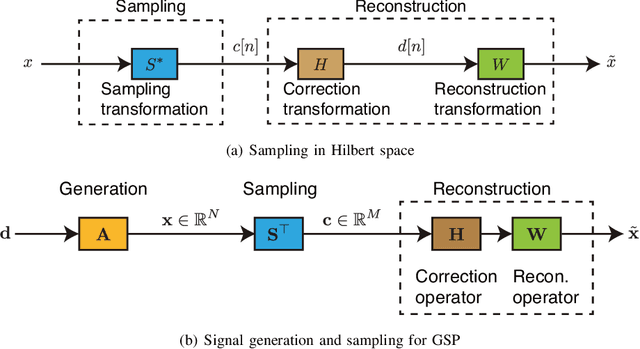
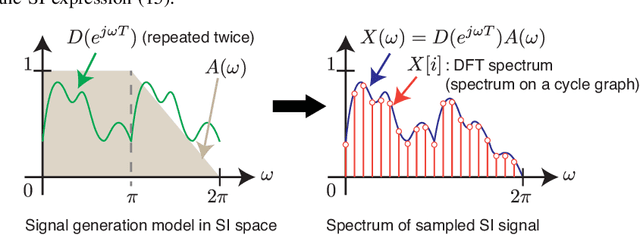
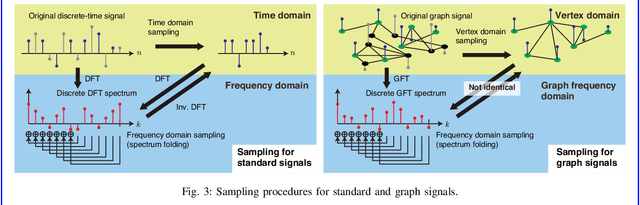
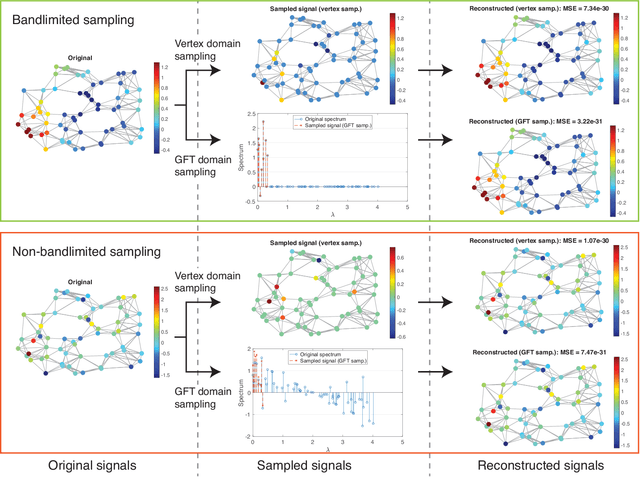
The study of sampling signals on graphs, with the goal of building an analog of sampling for standard signals in the time and spatial domains, has attracted considerable attention recently. Beyond adding to the growing theory on graph signal processing (GSP), sampling on graphs has various promising applications. In this article, we review current progress on sampling over graphs focusing on theory and potential applications. Most methodologies used in graph signal sampling are designed to parallel those used in sampling for standard signals, however, sampling theory for graph signals significantly differs from that for Shannon--Nyquist and shift invariant signals. This is due in part to the fact that the definitions of several important properties, such as shift invariance and bandlimitedness, are different in GSP systems. Throughout, we discuss similarities and differences between standard and graph sampling and highlight open problems and challenges.

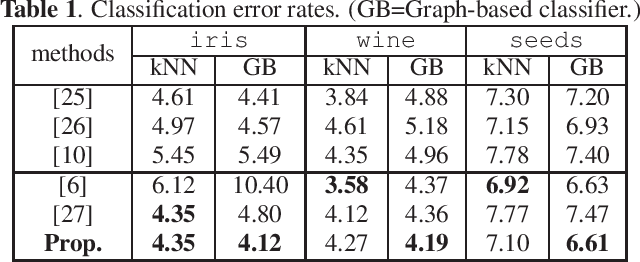
Graph Metric Learning via Gershgorin Disc Alignment

We propose a fast general projection-free metric learning framework, where the minimization objective $\min_{\textbf{M} \in \mathcal{S}} Q(\textbf{M})$ is a convex differentiable function of the metric matrix $\textbf{M}$, and $\textbf{M}$ resides in the set $\mathcal{S}$ of generalized graph Laplacian matrices for connected graphs with positive edge weights and node degrees. Unlike low-rank metric matrices common in the literature, $\mathcal{S}$ includes the important positive-diagonal-only matrices as a special case in the limit. The key idea for fast optimization is to rewrite the positive definite cone constraint in $\mathcal{S}$ as signal-adaptive linear constraints via Gershgorin disc alignment, so that the alternating optimization of the diagonal and off-diagonal terms in $\textbf{M}$ can be solved efficiently as linear programs via Frank-Wolfe iterations. We prove that the Gershgorin discs can be aligned perfectly using the first eigenvector $\textbf{v}$ of $\textbf{M}$, which we update iteratively using Locally Optimal Block Preconditioned Conjugate Gradient (LOBPCG) with warm start as diagonal / off-diagonal terms are optimized. Experiments show that our efficiently computed graph metric matrices outperform metrics learned using competing methods in terms of classification tasks.

Robust Deep Graph Based Learning for Binary Classification

Convolutional neural network (CNN)-based feature learning has become state of the art, since given sufficient training data, CNN can significantly outperform traditional methods for various classification tasks. However, feature learning becomes more difficult if some training labels are noisy. With traditional regularization techniques, CNN often overfits to the noisy training labels, resulting in sub-par classification performance. In this paper, we propose a robust binary classifier, based on CNNs, to learn deep metric functions, which are then used to construct an optimal underlying graph structure used to clean noisy labels via graph Laplacian regularization (GLR). GLR is posed as a convex maximum a posteriori (MAP) problem solved via convex quadratic programming (QP). To penalize samples around the decision boundary, we propose two regularized loss functions for semi-supervised learning. The binary classification experiments on three datasets, varying in number and type of features, demonstrate that given a noisy training dataset, our proposed networks outperform several state-of-the-art classifiers, including label-noise robust support vector machine, CNNs with three different robust loss functions, model-based GLR, and dynamic graph CNN classifiers.

Feature Graph Learning for 3D Point Cloud Denoising

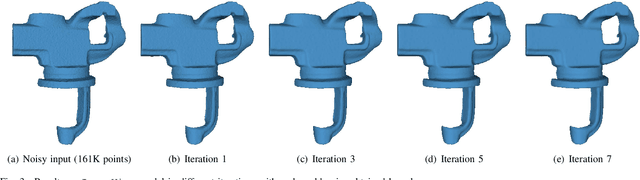
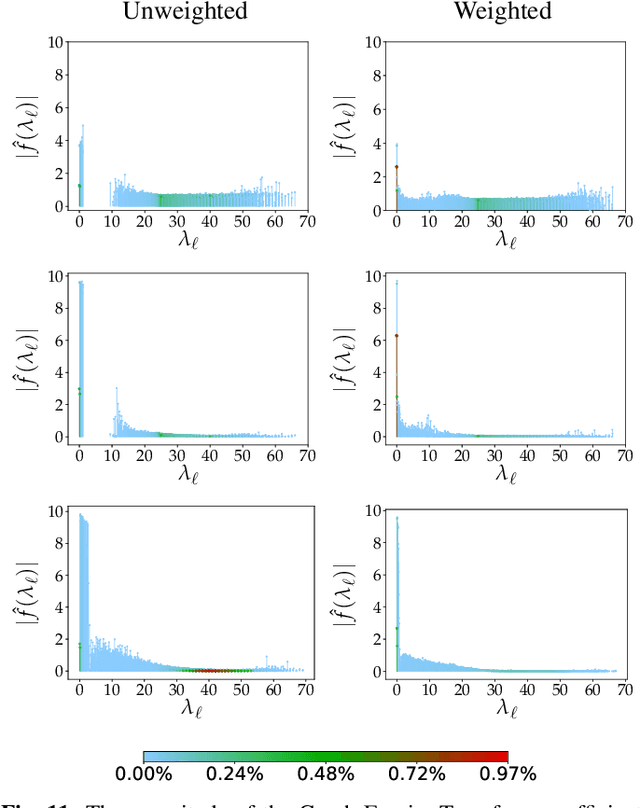
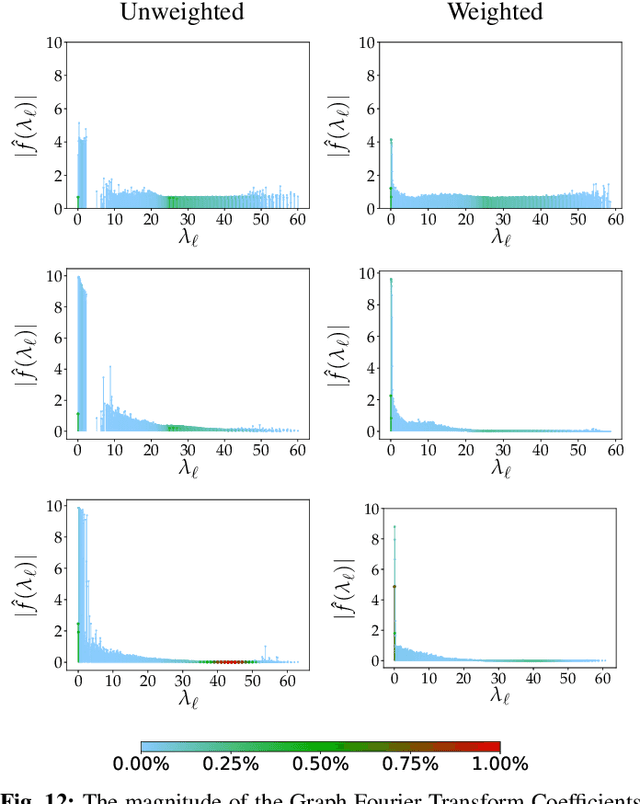
Identifying an appropriate underlying graph kernel that reflects pairwise similarities is critical in many recent graph spectral signal restoration schemes, including image denoising, dequantization, and contrast enhancement. Existing graph learning algorithms compute the most likely entries of a properly defined graph Laplacian matrix $\mathbf{L}$, but require a large number of signal observations $\mathbf{z}$'s for a stable estimate. In this work, we assume instead the availability of a relevant feature vector $\mathbf{f}_i$ per node $i$, from which we compute an optimal feature graph via optimization of a feature metric. Specifically, we alternately optimize the diagonal and off-diagonal entries of a Mahalanobis distance matrix $\mathbf{M}$ by minimizing the graph Laplacian regularizer (GLR) $\mathbf{z}^{\top} \mathbf{L} \mathbf{z}$, where edge weight is $w_{i,j} = \exp\{-(\mathbf{f}_i - \mathbf{f}_j)^{\top} \mathbf{M} (\mathbf{f}_i - \mathbf{f}_j) \}$, given a single observation $\mathbf{z}$. We optimize diagonal entries via proximal gradient (PG), where we constrain $\mathbf{M}$ to be positive definite (PD) via linear inequalities derived from the Gershgorin circle theorem. To optimize off-diagonal entries, we design a block descent algorithm that iteratively optimizes one row and column of $\mathbf{M}$. To keep $\mathbf{M}$ PD, we constrain the Schur complement of sub-matrix $\mathbf{M}_{2,2}$ of $\mathbf{M}$ to be PD when optimizing via PG. Our algorithm mitigates full eigen-decomposition of $\mathbf{M}$, thus ensuring fast computation speed even when feature vector $\mathbf{f}_i$ has high dimension. To validate its usefulness, we apply our feature graph learning algorithm to the problem of 3D point cloud denoising, resulting in state-of-the-art performance compared to competing schemes in extensive experiments.

Deep Graph Laplacian Regularization

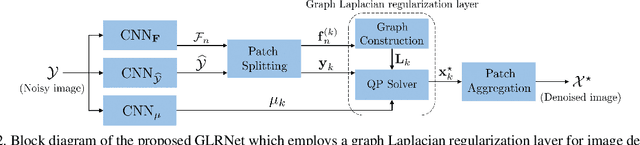
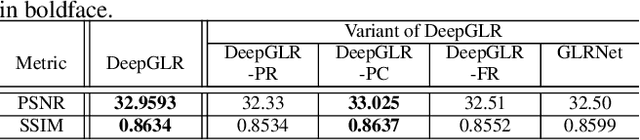
We propose to combine the robustness merit of model-based approaches and the learning power of data-driven approaches for image restoration. Specifically, by integrating graph Laplacian regularization as a trainable module into a deep learning framework, we are less susceptible to overfitting than pure CNN-based approaches, achieving higher robustness to small dataset and cross-domain denoising. First, a sparse neighborhood graph is built from the output of a convolutional neural network (CNN). Then the image is restored by solving an unconstrained quadratic programming problem, using a corresponding graph Laplacian regularizer as a prior term. The proposed restoration pipeline is fully differentiable and hence can be end-to-end trained. Experimental results demonstrate that our work avoids overfitting given small training data. It is also endowed with strong cross-domain generalization power, outperforming the state-of-the-art approaches by remarkable margin.

SiGAN: Siamese Generative Adversarial Network for Identity-Preserving Face Hallucination

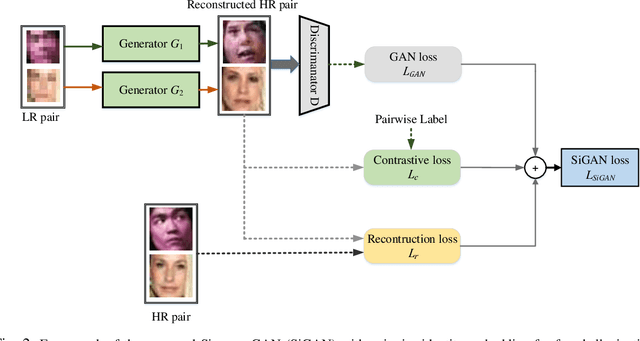
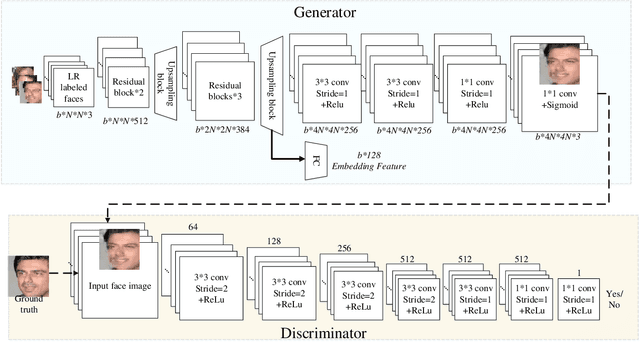
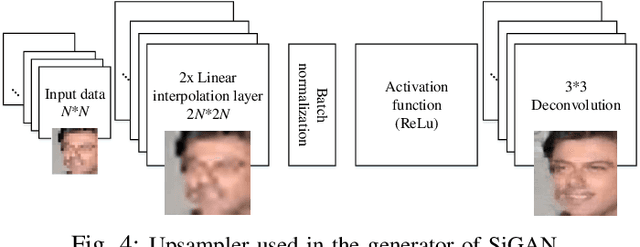
Despite generative adversarial networks (GANs) can hallucinate photo-realistic high-resolution (HR) faces from low-resolution (LR) faces, they cannot guarantee preserving the identities of hallucinated HR faces, making the HR faces poorly recognizable. To address this problem, we propose a Siamese GAN (SiGAN) to reconstruct HR faces that visually resemble their corresponding identities. On top of a Siamese network, the proposed SiGAN consists of a pair of two identical generators and one discriminator. We incorporate reconstruction error and identity label information in the loss function of SiGAN in a pairwise manner. By iteratively optimizing the loss functions of the generator pair and discriminator of SiGAN, we cannot only achieve photo-realistic face reconstruction, but also ensures the reconstructed information is useful for identity recognition. Experimental results demonstrate that SiGAN significantly outperforms existing face hallucination GANs in objective face verification performance, while achieving photo-realistic reconstruction. Moreover, for input LR faces from unknown identities who are not included in training, SiGAN can still do a good job.