Fu-Dong Wang
Holistically-Attracted Wireframe Parsing: From Supervised to Self-Supervised Learning
Oct 24, 2022Abstract:This paper presents Holistically-Attracted Wireframe Parsing (HAWP) for 2D images using both fully supervised and self-supervised learning paradigms. At the core is a parsimonious representation that encodes a line segment using a closed-form 4D geometric vector, which enables lifting line segments in wireframe to an end-to-end trainable holistic attraction field that has built-in geometry-awareness, context-awareness and robustness. The proposed HAWP consists of three components: generating line segment and end-point proposal, binding line segment and end-point, and end-point-decoupled lines-of-interest verification. For self-supervised learning, a simulation-to-reality pipeline is exploited in which a HAWP is first trained using synthetic data and then used to ``annotate" wireframes in real images with Homographic Adaptation. With the self-supervised annotations, a HAWP model for real images is trained from scratch. In experiments, the proposed HAWP achieves state-of-the-art performance in both the Wireframe dataset and the YorkUrban dataset in fully-supervised learning. It also demonstrates a significantly better repeatability score than prior arts with much more efficient training in self-supervised learning. Furthermore, the self-supervised HAWP shows great potential for general wireframe parsing without onerous wireframe labels.
Holistically-Attracted Wireframe Parsing
Mar 03, 2020
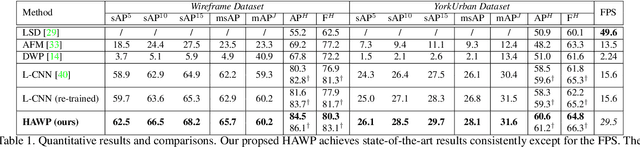
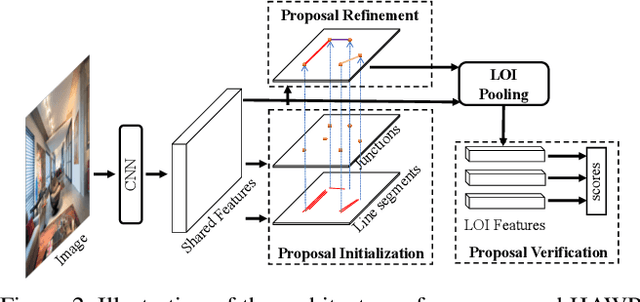
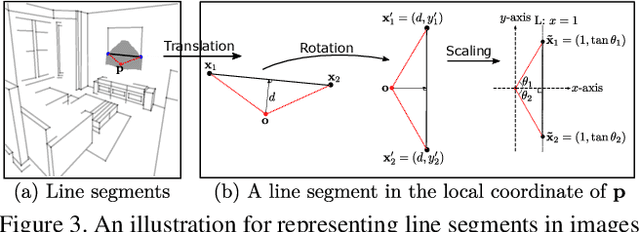
Abstract:This paper presents a fast and parsimonious parsing method to accurately and robustly detect a vectorized wireframe in an input image with a single forward pass. The proposed method is end-to-end trainable, consisting of three components: (i) line segment and junction proposal generation, (ii) line segment and junction matching, and (iii) line segment and junction verification. For computing line segment proposals, a novel exact dual representation is proposed which exploits a parsimonious geometric reparameterization for line segments and forms a holistic 4-dimensional attraction field map for an input image. Junctions can be treated as the "basins" in the attraction field. The proposed method is thus called Holistically-Attracted Wireframe Parser (HAWP). In experiments, the proposed method is tested on two benchmarks, the Wireframe dataset, and the YorkUrban dataset. On both benchmarks, it obtains state-of-the-art performance in terms of accuracy and efficiency. For example, on the Wireframe dataset, compared to the previous state-of-the-art method L-CNN, it improves the challenging mean structural average precision (msAP) by a large margin ($2.8\%$ absolute improvements) and achieves 29.5 FPS on single GPU ($89\%$ relative improvement). A systematic ablation study is performed to further justify the proposed method.
Learning Regional Attraction for Line Segment Detection
Dec 18, 2019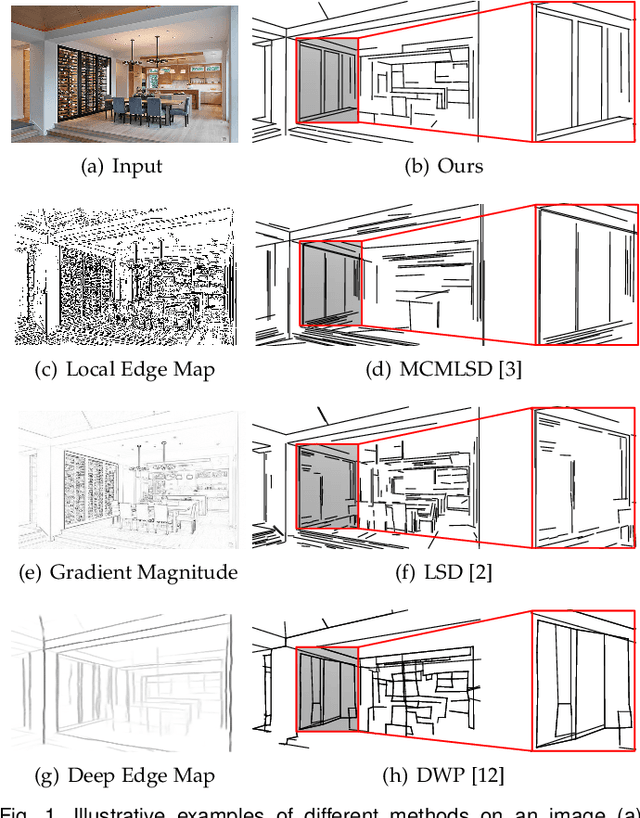
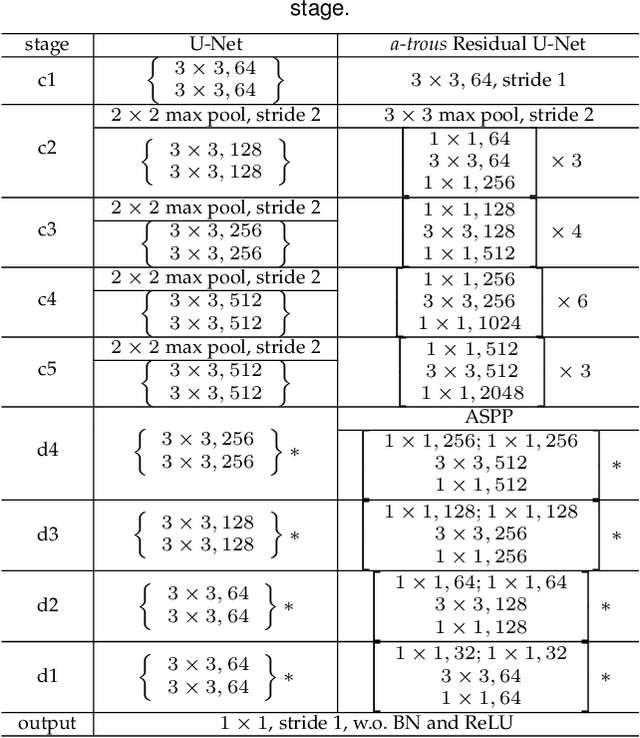
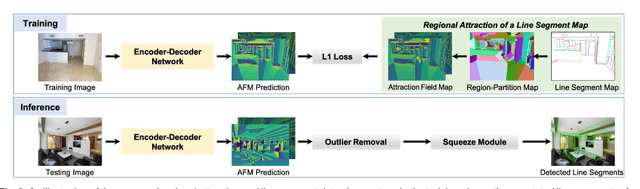
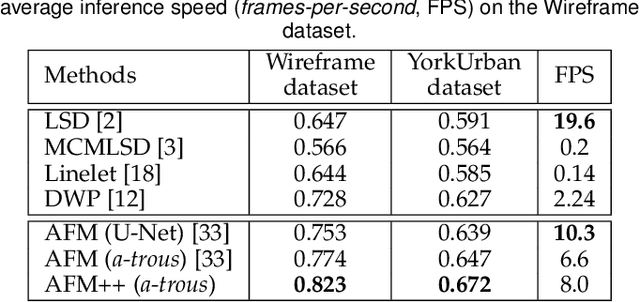
Abstract:This paper presents regional attraction of line segment maps, and hereby poses the problem of line segment detection (LSD) as a problem of region coloring. Given a line segment map, the proposed regional attraction first establishes the relationship between line segments and regions in the image lattice. Based on this, the line segment map is equivalently transformed to an attraction field map (AFM), which can be remapped to a set of line segments without loss of information. Accordingly, we develop an end-to-end framework to learn attraction field maps for raw input images, followed by a squeeze module to detect line segments. Apart from existing works, the proposed detector properly handles the local ambiguity and does not rely on the accurate identification of edge pixels. Comprehensive experiments on the Wireframe dataset and the YorkUrban dataset demonstrate the superiority of our method. In particular, we achieve an F-measure of 0.831 on the Wireframe dataset, advancing the state-of-the-art performance by 10.3 percent.
A Functional Representation for Graph Matching
Jan 16, 2019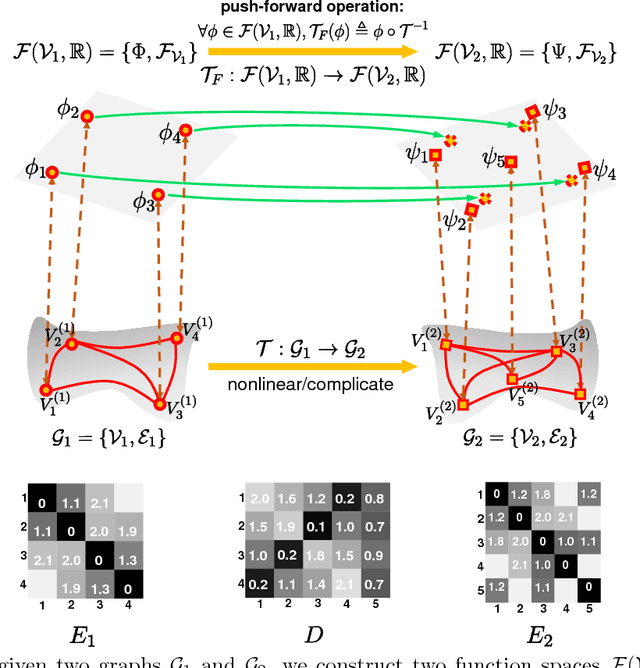
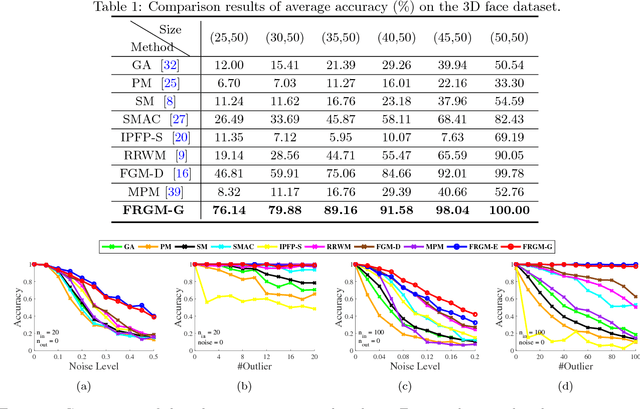
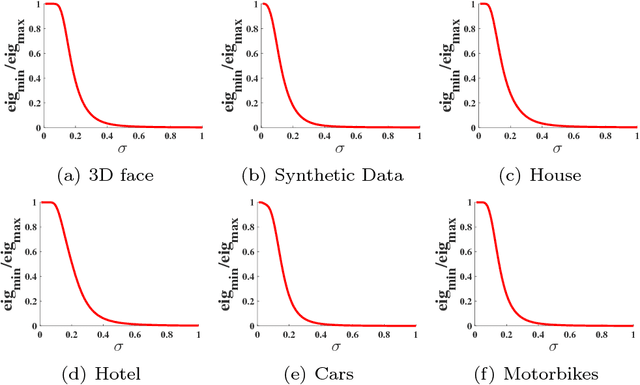
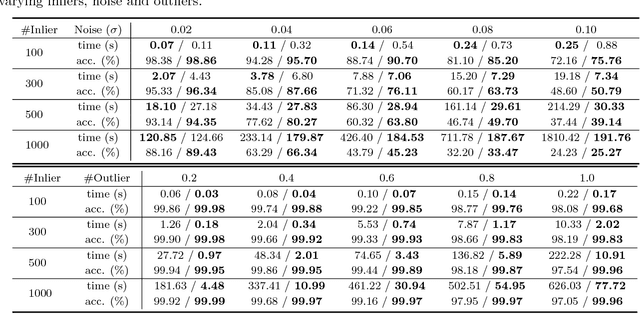
Abstract:Graph matching is an important and persistent problem in computer vision and pattern recognition for finding node-to-node correspondence between graph-structured data. However, as widely used, graph matching that incorporates pairwise constraints can be formulated as a quadratic assignment problem (QAP), which is NP-complete and results in intrinsic computational difficulties. In this paper, we present a functional representation for graph matching (FRGM) that aims to provide more geometric insights on the problem and reduce the space and time complexities of corresponding algorithms. To achieve these goals, we represent a graph endowed with edge attributes by a linear function space equipped with a functional such as inner product or metric, that has an explicit geometric meaning. Consequently, the correspondence between graphs can be represented as a linear representation map of that functional. Specifically, we reformulate the linear functional representation map as a new parameterization for Euclidean graph matching, which is associative with geometric parameters for graphs under rigid or nonrigid deformations. This allows us to estimate the correspondence and geometric deformations simultaneously. The use of the representation of edge attributes rather than the affinity matrix enables us to reduce the space complexity by two orders of magnitudes. Furthermore, we propose an efficient optimization strategy with low time complexity to optimize the objective function. The experimental results on both synthetic and real-world datasets demonstrate that the proposed FRGM can achieve state-of-the-art performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge