Quantum Theory and Application of Contextual Optimal Transport

Optimal Transport (OT) has fueled machine learning (ML) applications across many domains. In cases where paired data measurements ($\mu$, $\nu$) are coupled to a context variable $p_i$ , one may aspire to learn a global transportation map that can be parameterized through a potentially unseen con-text. Existing approaches utilize Neural OT and largely rely on Brenier's theorem. Here, we propose a first-of-its-kind quantum computing formulation for amortized optimization of contextualized transportation plans. We exploit a direct link between doubly stochastic matrices and unitary operators thus finding a natural connection between OT and quantum computation. We verify our method on synthetic and real data, by predicting variations in cell type distributions parameterized through drug dosage as context. Our comparisons to several baselines reveal that our method can capture dose-induced variations in cell distributions, even to some extent when dosages are extrapolated and sometimes with performance similar to the best classical models. In summary, this is a first step toward learning to predict contextualized transportation plans through quantum.

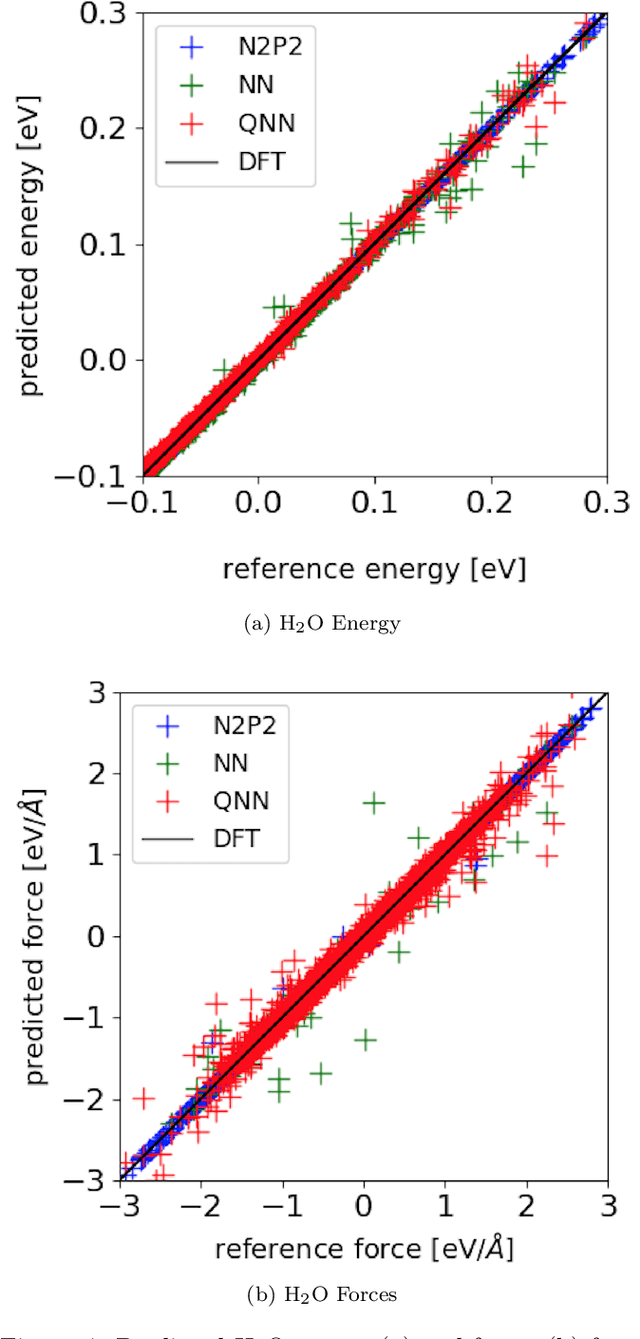
Symmetry-invariant quantum machine learning force fields

Machine learning techniques are essential tools to compute efficient, yet accurate, force fields for atomistic simulations. This approach has recently been extended to incorporate quantum computational methods, making use of variational quantum learning models to predict potential energy surfaces and atomic forces from ab initio training data. However, the trainability and scalability of such models are still limited, due to both theoretical and practical barriers. Inspired by recent developments in geometric classical and quantum machine learning, here we design quantum neural networks that explicitly incorporate, as a data-inspired prior, an extensive set of physically relevant symmetries. We find that our invariant quantum learning models outperform their more generic counterparts on individual molecules of growing complexity. Furthermore, we study a water dimer as a minimal example of a system with multiple components, showcasing the versatility of our proposed approach and opening the way towards larger simulations. Our results suggest that molecular force fields generation can significantly profit from leveraging the framework of geometric quantum machine learning, and that chemical systems represent, in fact, an interesting and rich playground for the development and application of advanced quantum machine learning tools.

Unravelling physics beyond the standard model with classical and quantum anomaly detection

Much hope for finding new physics phenomena at microscopic scale relies on the observations obtained from High Energy Physics experiments, like the ones performed at the Large Hadron Collider (LHC). However, current experiments do not indicate clear signs of new physics that could guide the development of additional Beyond Standard Model (BSM) theories. Identifying signatures of new physics out of the enormous amount of data produced at the LHC falls into the class of anomaly detection and constitutes one of the greatest computational challenges. In this article, we propose a novel strategy to perform anomaly detection in a supervised learning setting, based on the artificial creation of anomalies through a random process. For the resulting supervised learning problem, we successfully apply classical and quantum Support Vector Classifiers (CSVC and QSVC respectively) to identify the artificial anomalies among the SM events. Even more promising, we find that employing an SVC trained to identify the artificial anomalies, it is possible to identify realistic BSM events with high accuracy. In parallel, we also explore the potential of quantum algorithms for improving the classification accuracy and provide plausible conditions for the best exploitation of this novel computational paradigm.

Quantum Machine Learning Framework for Virtual Screening in Drug Discovery: a Prospective Quantum Advantage

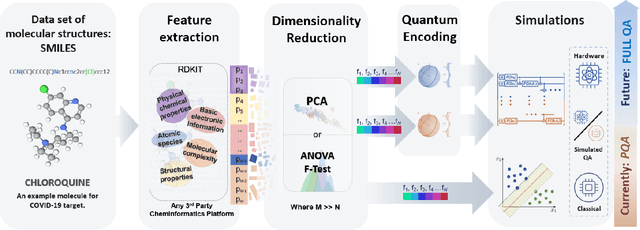
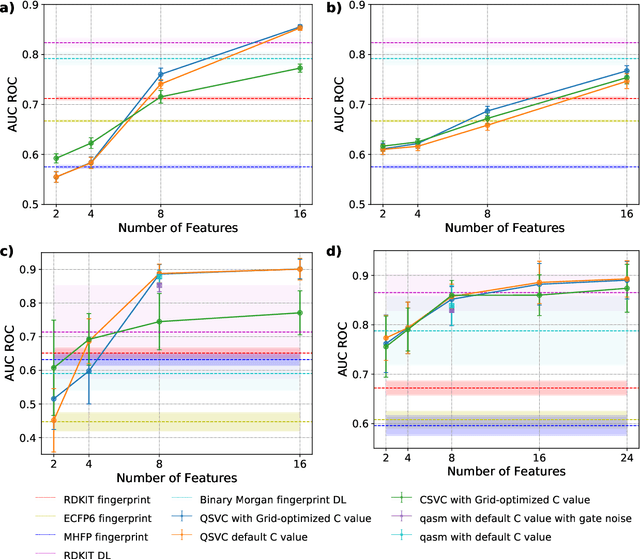
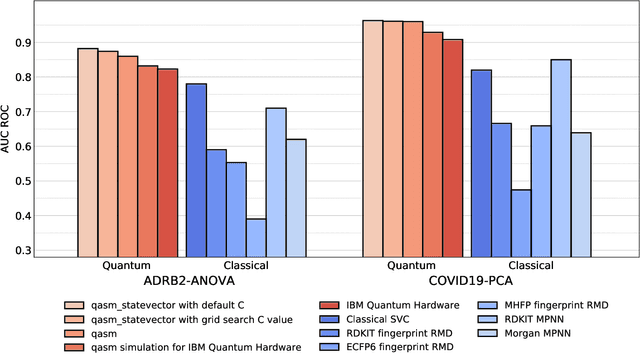
Machine Learning (ML) for Ligand Based Virtual Screening (LB-VS) is an important in-silico tool for discovering new drugs in a faster and cost-effective manner, especially for emerging diseases such as COVID-19. In this paper, we propose a general-purpose framework combining a classical Support Vector Classifier (SVC) algorithm with quantum kernel estimation for LB-VS on real-world databases, and we argue in favor of its prospective quantum advantage. Indeed, we heuristically prove that our quantum integrated workflow can, at least in some relevant instances, provide a tangible advantage compared to state-of-art classical algorithms operating on the same datasets, showing strong dependence on target and features selection method. Finally, we test our algorithm on IBM Quantum processors using ADRB2 and COVID-19 datasets, showing that hardware simulations provide results in line with the predicted performances and can surpass classical equivalents.

An analytic theory for the dynamics of wide quantum neural networks

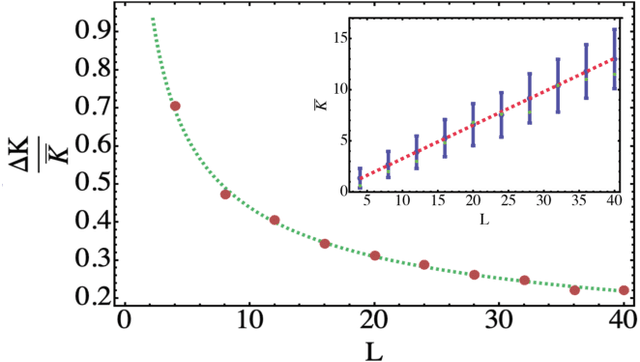
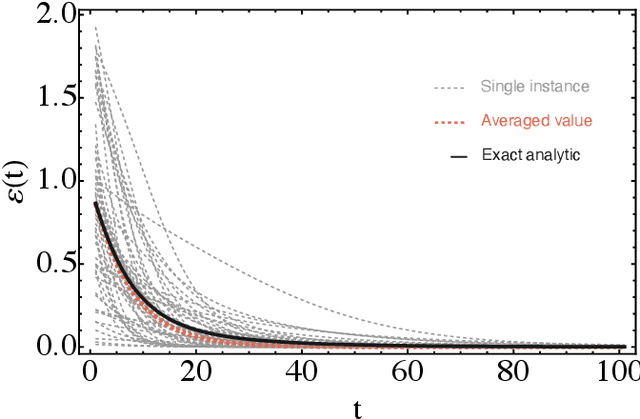
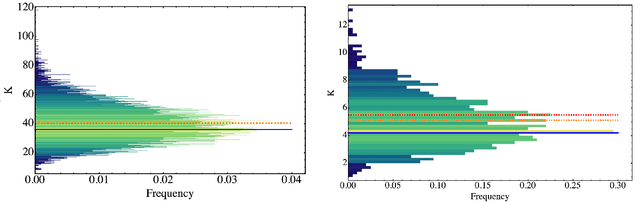
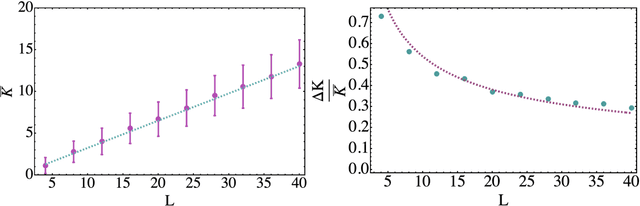
Parametrized quantum circuits can be used as quantum neural networks and have the potential to outperform their classical counterparts when trained for addressing learning problems. To date, much of the results on their performance on practical problems are heuristic in nature. In particular, the convergence rate for the training of quantum neural networks is not fully understood. Here, we analyze the dynamics of gradient descent for the training error of a class of variational quantum machine learning models. We define wide quantum neural networks as parameterized quantum circuits in the limit of a large number of qubits and variational parameters. We then find a simple analytic formula that captures the average behavior of their loss function and discuss the consequences of our findings. For example, for random quantum circuits, we predict and characterize an exponential decay of the residual training error as a function of the parameters of the system. We finally validate our analytic results with numerical experiments.

Quantum neural networks force fields generation

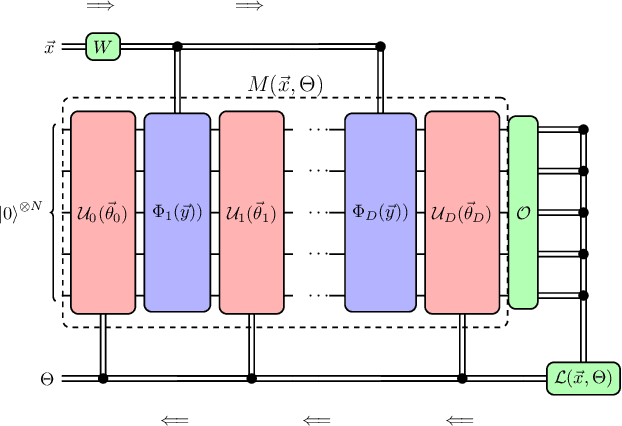
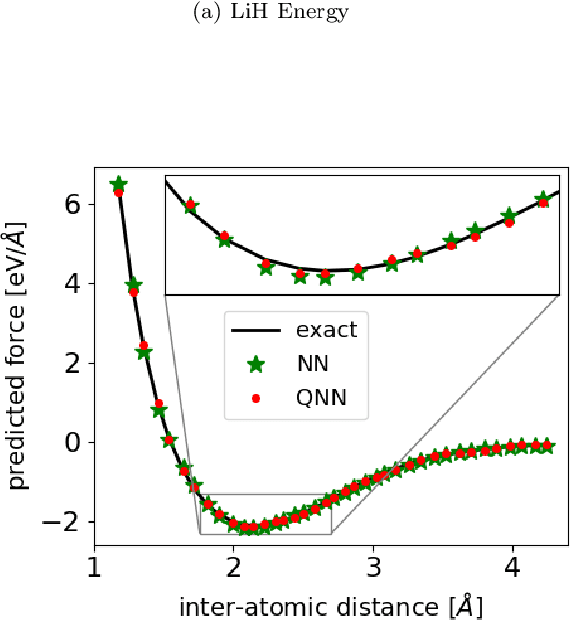
Accurate molecular force fields are of paramount importance for the efficient implementation of molecular dynamics techniques at large scales. In the last decade, machine learning methods have demonstrated impressive performances in predicting accurate values for energy and forces when trained on finite size ensembles generated with ab initio techniques. At the same time, quantum computers have recently started to offer new viable computational paradigms to tackle such problems. On the one hand, quantum algorithms may notably be used to extend the reach of electronic structure calculations. On the other hand, quantum machine learning is also emerging as an alternative and promising path to quantum advantage. Here we follow this second route and establish a direct connection between classical and quantum solutions for learning neural network potentials. To this end, we design a quantum neural network architecture and apply it successfully to different molecules of growing complexity. The quantum models exhibit larger effective dimension with respect to classical counterparts and can reach competitive performances, thus pointing towards potential quantum advantages in natural science applications via quantum machine learning.

Representation Learning via Quantum Neural Tangent Kernels

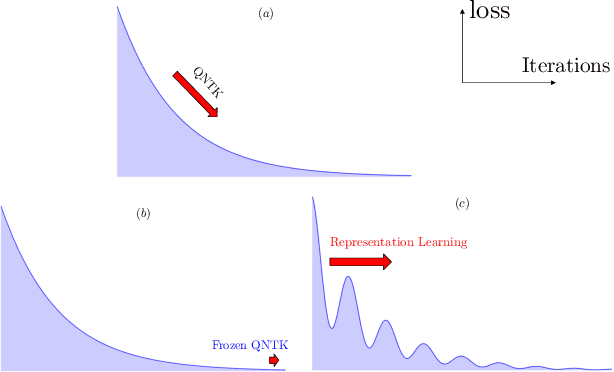
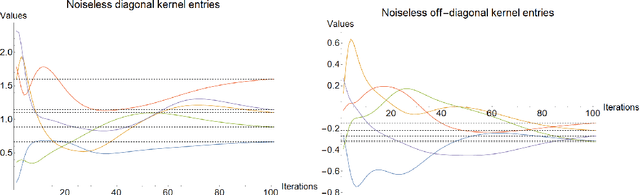
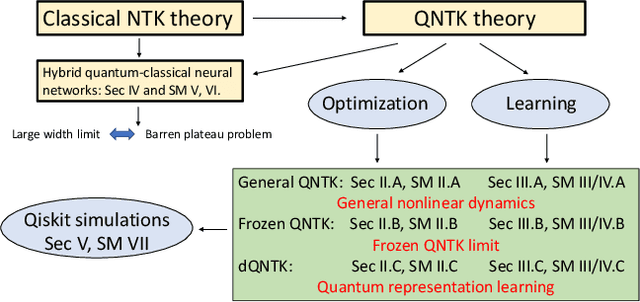
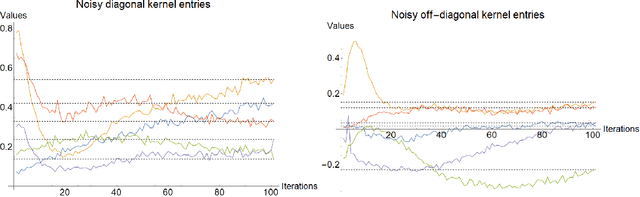
Variational quantum circuits are used in quantum machine learning and variational quantum simulation tasks. Designing good variational circuits or predicting how well they perform for given learning or optimization tasks is still unclear. Here we discuss these problems, analyzing variational quantum circuits using the theory of neural tangent kernels. We define quantum neural tangent kernels, and derive dynamical equations for their associated loss function in optimization and learning tasks. We analytically solve the dynamics in the frozen limit, or lazy training regime, where variational angles change slowly and a linear perturbation is good enough. We extend the analysis to a dynamical setting, including quadratic corrections in the variational angles. We then consider hybrid quantum-classical architecture and define a large-width limit for hybrid kernels, showing that a hybrid quantum-classical neural network can be approximately Gaussian. The results presented here show limits for which analytical understandings of the training dynamics for variational quantum circuits, used for quantum machine learning and optimization problems, are possible. These analytical results are supported by numerical simulations of quantum machine learning experiments.