Symmetry-invariant quantum machine learning force fields

Machine learning techniques are essential tools to compute efficient, yet accurate, force fields for atomistic simulations. This approach has recently been extended to incorporate quantum computational methods, making use of variational quantum learning models to predict potential energy surfaces and atomic forces from ab initio training data. However, the trainability and scalability of such models are still limited, due to both theoretical and practical barriers. Inspired by recent developments in geometric classical and quantum machine learning, here we design quantum neural networks that explicitly incorporate, as a data-inspired prior, an extensive set of physically relevant symmetries. We find that our invariant quantum learning models outperform their more generic counterparts on individual molecules of growing complexity. Furthermore, we study a water dimer as a minimal example of a system with multiple components, showcasing the versatility of our proposed approach and opening the way towards larger simulations. Our results suggest that molecular force fields generation can significantly profit from leveraging the framework of geometric quantum machine learning, and that chemical systems represent, in fact, an interesting and rich playground for the development and application of advanced quantum machine learning tools.

Hybrid Ground-State Quantum Algorithms based on Neural Schrödinger Forging

Entanglement forging based variational algorithms leverage the bi-partition of quantum systems for addressing ground state problems. The primary limitation of these approaches lies in the exponential summation required over the numerous potential basis states, or bitstrings, when performing the Schmidt decomposition of the whole system. To overcome this challenge, we propose a new method for entanglement forging employing generative neural networks to identify the most pertinent bitstrings, eliminating the need for the exponential sum. Through empirical demonstrations on systems of increasing complexity, we show that the proposed algorithm achieves comparable or superior performance compared to the existing standard implementation of entanglement forging. Moreover, by controlling the amount of required resources, this scheme can be applied to larger, as well as non permutation invariant systems, where the latter constraint is associated with the Heisenberg forging procedure. We substantiate our findings through numerical simulations conducted on spins models exhibiting one-dimensional ring, two-dimensional triangular lattice topologies, and nuclear shell model configurations.

Trainability barriers and opportunities in quantum generative modeling

Quantum generative models, in providing inherently efficient sampling strategies, show promise for achieving a near-term advantage on quantum hardware. Nonetheless, important questions remain regarding their scalability. In this work, we investigate the barriers to the trainability of quantum generative models posed by barren plateaus and exponential loss concentration. We explore the interplay between explicit and implicit models and losses, and show that using implicit generative models (such as quantum circuit-based models) with explicit losses (such as the KL divergence) leads to a new flavour of barren plateau. In contrast, the Maximum Mean Discrepancy (MMD), which is a popular example of an implicit loss, can be viewed as the expectation value of an observable that is either low-bodied and trainable, or global and untrainable depending on the choice of kernel. However, in parallel, we highlight that the low-bodied losses required for trainability cannot in general distinguish high-order correlations, leading to a fundamental tension between exponential concentration and the emergence of spurious minima. We further propose a new local quantum fidelity-type loss which, by leveraging quantum circuits to estimate the quality of the encoded distribution, is both faithful and enjoys trainability guarantees. Finally, we compare the performance of different loss functions for modelling real-world data from the High-Energy-Physics domain and confirm the trends predicted by our theoretical results.

Conditional Born machine for Monte Carlo events generation

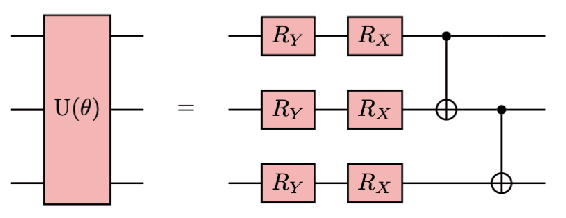
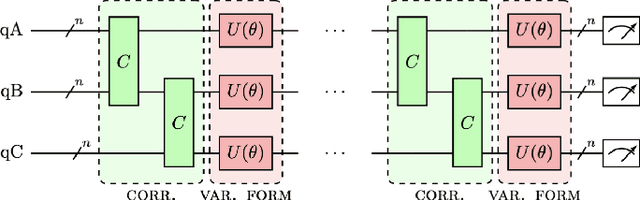
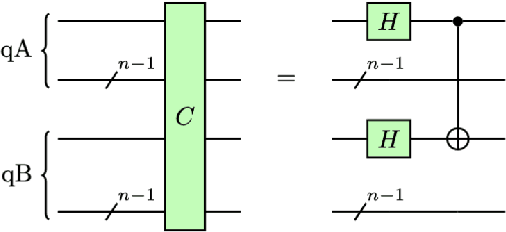
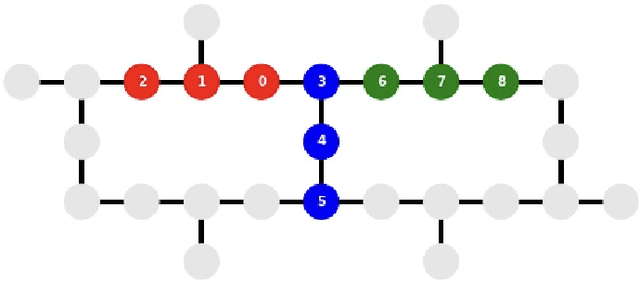
Generative modeling is a promising task for near-term quantum devices, which can use the stochastic nature of quantum measurements as random source. So called Born machines are purely quantum models and promise to generate probability distributions in a quantum way, inaccessible to classical computers. This paper presents an application of Born machines to Monte Carlo simulations and extends their reach to multivariate and conditional distributions. Models are run on (noisy) simulators and IBM Quantum superconducting quantum hardware. More specifically, Born machines are used to generate muonic force carriers (MFC) events resulting from scattering processes between muons and the detector material in high-energy-physics colliders experiments. MFCs are bosons appearing in beyond the standard model theoretical frameworks, which are candidates for dark matter. Empirical evidences suggest that Born machines can reproduce the underlying distribution of datasets coming from Monte Carlo simulations, and are competitive with classical machine learning-based generative models of similar complexity.

Quantum neural networks force fields generation

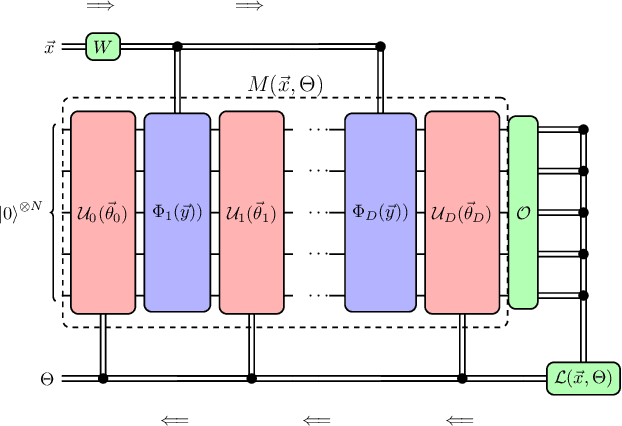
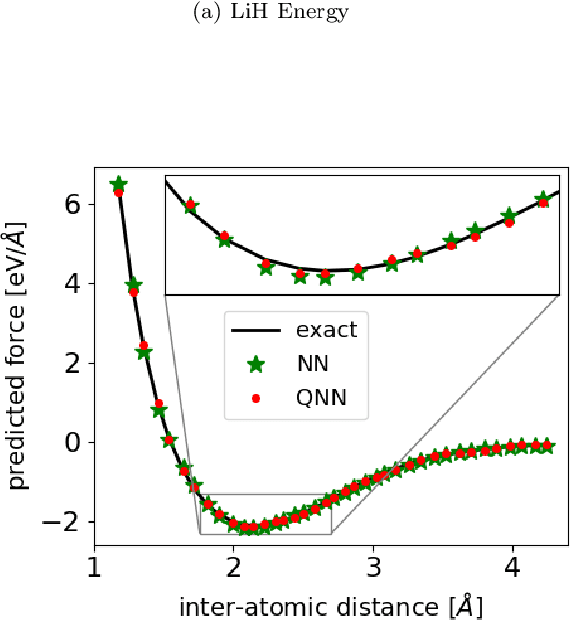
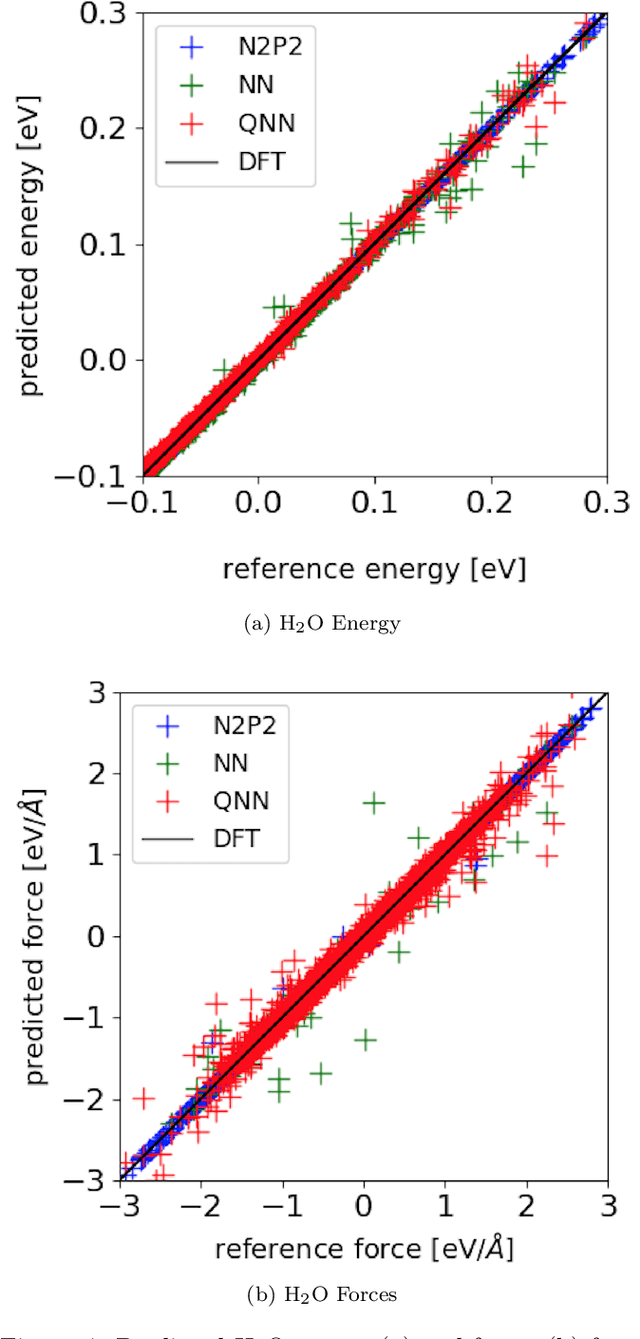
Accurate molecular force fields are of paramount importance for the efficient implementation of molecular dynamics techniques at large scales. In the last decade, machine learning methods have demonstrated impressive performances in predicting accurate values for energy and forces when trained on finite size ensembles generated with ab initio techniques. At the same time, quantum computers have recently started to offer new viable computational paradigms to tackle such problems. On the one hand, quantum algorithms may notably be used to extend the reach of electronic structure calculations. On the other hand, quantum machine learning is also emerging as an alternative and promising path to quantum advantage. Here we follow this second route and establish a direct connection between classical and quantum solutions for learning neural network potentials. To this end, we design a quantum neural network architecture and apply it successfully to different molecules of growing complexity. The quantum models exhibit larger effective dimension with respect to classical counterparts and can reach competitive performances, thus pointing towards potential quantum advantages in natural science applications via quantum machine learning.