Reproducing Kernel Hilbert Space, Mercer's Theorem, Eigenfunctions, Nyström Method, and Use of Kernels in Machine Learning: Tutorial and Survey

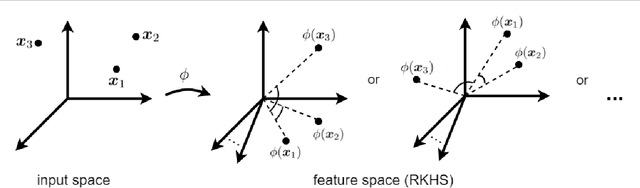
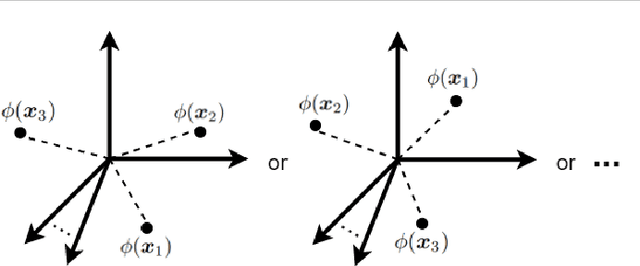
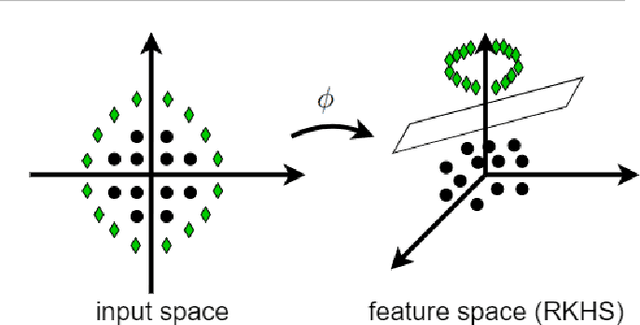
This is a tutorial and survey paper on kernels, kernel methods, and related fields. We start with reviewing the history of kernels in functional analysis and machine learning. Then, Mercer kernel, Hilbert and Banach spaces, Reproducing Kernel Hilbert Space (RKHS), Mercer's theorem and its proof, frequently used kernels, kernel construction from distance metric, important classes of kernels (including bounded, integrally positive definite, universal, stationary, and characteristic kernels), kernel centering and normalization, and eigenfunctions are explained in detail. Then, we introduce types of use of kernels in machine learning including kernel methods (such as kernel support vector machines), kernel learning by semi-definite programming, Hilbert-Schmidt independence criterion, maximum mean discrepancy, kernel mean embedding, and kernel dimensionality reduction. We also cover rank and factorization of kernel matrix as well as the approximation of eigenfunctions and kernels using the Nystr{\"o}m method. This paper can be useful for various fields of science including machine learning, dimensionality reduction, functional analysis in mathematics, and mathematical physics in quantum mechanics.

Laplacian-Based Dimensionality Reduction Including Spectral Clustering, Laplacian Eigenmap, Locality Preserving Projection, Graph Embedding, and Diffusion Map: Tutorial and Survey

This is a tutorial and survey paper for nonlinear dimensionality and feature extraction methods which are based on the Laplacian of graph of data. We first introduce adjacency matrix, definition of Laplacian matrix, and the interpretation of Laplacian. Then, we cover the cuts of graph and spectral clustering which applies clustering in a subspace of data. Different optimization variants of Laplacian eigenmap and its out-of-sample extension are explained. Thereafter, we introduce the locality preserving projection and its kernel variant as linear special cases of Laplacian eigenmap. Versions of graph embedding are then explained which are generalized versions of Laplacian eigenmap and locality preserving projection. Finally, diffusion map is introduced which is a method based on Laplacian of data and random walks on the data graph.

UncertaintyFuseNet: Robust Uncertainty-aware Hierarchical Feature Fusion with Ensemble Monte Carlo Dropout for COVID-19 Detection

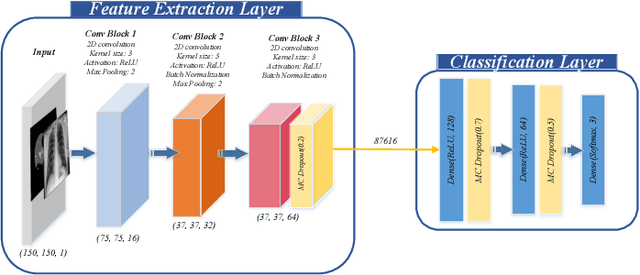
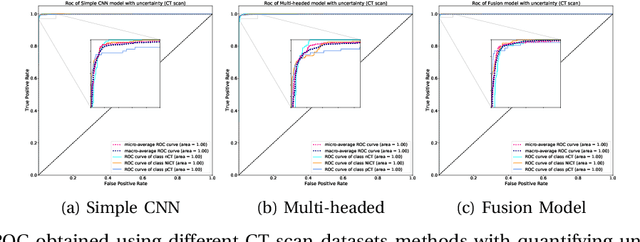
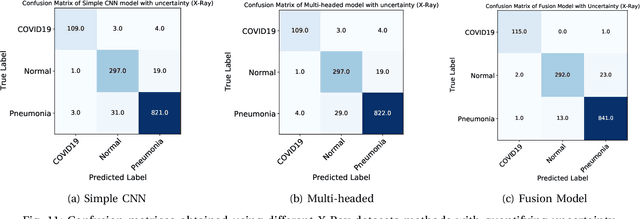
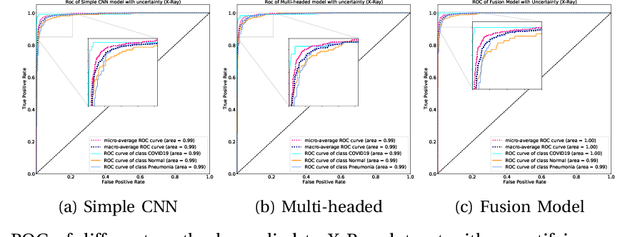
The COVID-19 (Coronavirus disease 2019) has infected more than 151 million people and caused approximately 3.17 million deaths around the world up to the present. The rapid spread of COVID-19 is continuing to threaten human's life and health. Therefore, the development of computer-aided detection (CAD) systems based on machine and deep learning methods which are able to accurately differentiate COVID-19 from other diseases using chest computed tomography (CT) and X-Ray datasets is essential and of immediate priority. Different from most of the previous studies which used either one of CT or X-ray images, we employed both data types with sufficient samples in implementation. On the other hand, due to the extreme sensitivity of this pervasive virus, model uncertainty should be considered, while most previous studies have overlooked it. Therefore, we propose a novel powerful fusion model named $UncertaintyFuseNet$ that consists of an uncertainty module: Ensemble Monte Carlo (EMC) dropout. The obtained results prove the effectiveness of our proposed fusion for COVID-19 detection using CT scan and X-Ray datasets. Also, our proposed $UncertaintyFuseNet$ model is significantly robust to noise and performs well with the previously unseen data. The source codes and models of this study are available at: https://github.com/moloud1987/UncertaintyFuseNet-for-COVID-19-Classification.

Generative Locally Linear Embedding

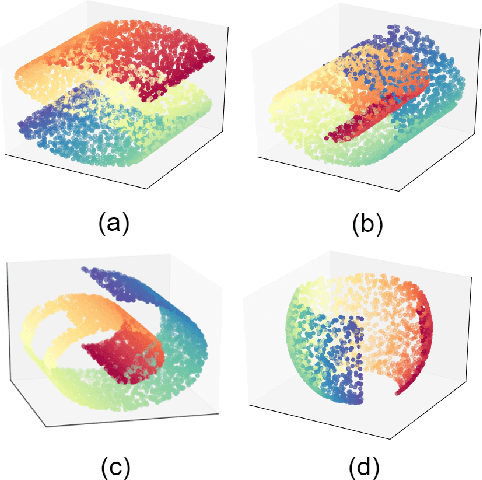
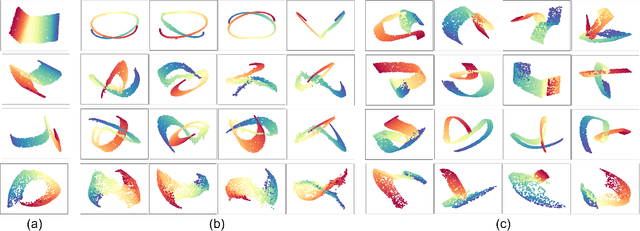
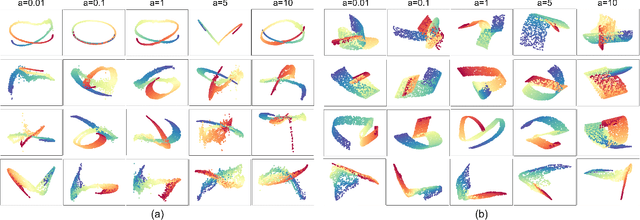
Locally Linear Embedding (LLE) is a nonlinear spectral dimensionality reduction and manifold learning method. It has two main steps which are linear reconstruction and linear embedding of points in the input space and embedding space, respectively. In this work, we propose two novel generative versions of LLE, named Generative LLE (GLLE), whose linear reconstruction steps are stochastic rather than deterministic. GLLE assumes that every data point is caused by its linear reconstruction weights as latent factors. The proposed GLLE algorithms can generate various LLE embeddings stochastically while all the generated embeddings relate to the original LLE embedding. We propose two versions for stochastic linear reconstruction, one using expectation maximization and another with direct sampling from a derived distribution by optimization. The proposed GLLE methods are closely related to and inspired by variational inference, factor analysis, and probabilistic principal component analysis. Our simulations show that the proposed GLLE methods work effectively in unfolding and generating submanifolds of data.

Deep Learning Approaches for Forecasting Strawberry Yields and Prices Using Satellite Images and Station-Based Soil Parameters

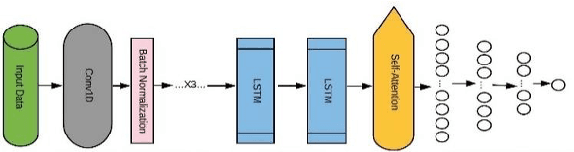
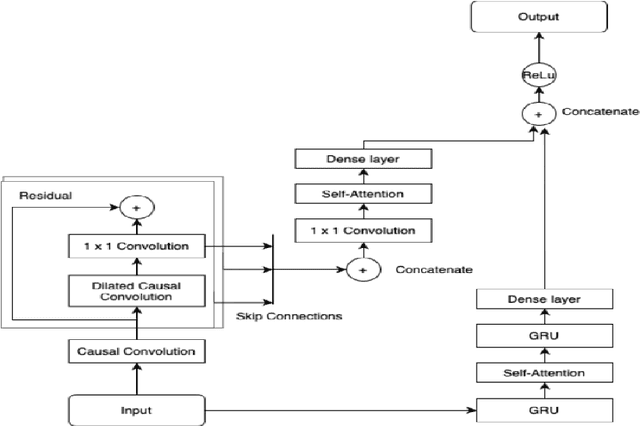
Computational tools for forecasting yields and prices for fresh produce have been based on traditional machine learning approaches or time series modelling. We propose here an alternate approach based on deep learning algorithms for forecasting strawberry yields and prices in Santa Barbara county, California. Building the proposed forecasting model comprises three stages: first, the station-based ensemble model (ATT-CNN-LSTM-SeriesNet_Ens) with its compound deep learning components, SeriesNet with Gated Recurrent Unit (GRU) and Convolutional Neural Network LSTM with Attention layer (Att-CNN-LSTM), are trained and tested using the station-based soil temperature and moisture data of SantaBarbara as input and the corresponding strawberry yields or prices as output. Secondly, the remote sensing ensemble model (SIM_CNN-LSTM_Ens), which is an ensemble model of Convolutional NeuralNetwork LSTM (CNN-LSTM) models, is trained and tested using satellite images of the same county as input mapped to the same yields and prices as output. These two ensembles forecast strawberry yields and prices with minimal forecasting errors and highest model correlation for five weeks ahead forecasts.Finally, the forecasts of these two models are ensembled to have a final forecasted value for yields and prices by introducing a voting ensemble. Based on an aggregated performance measure (AGM), it is found that this voting ensemble not only enhances the forecasting performance by 5% compared to its best performing component model but also outperforms the Deep Learning (DL) ensemble model found in literature by 33% for forecasting yields and 21% for forecasting prices

On the Philosophical, Cognitive and Mathematical Foundations of Symbiotic Autonomous Systems (SAS)

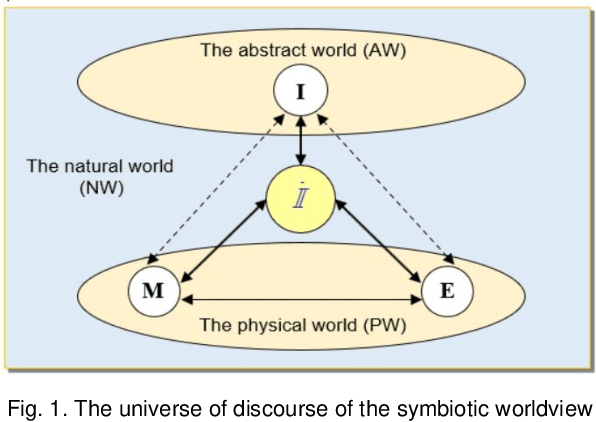
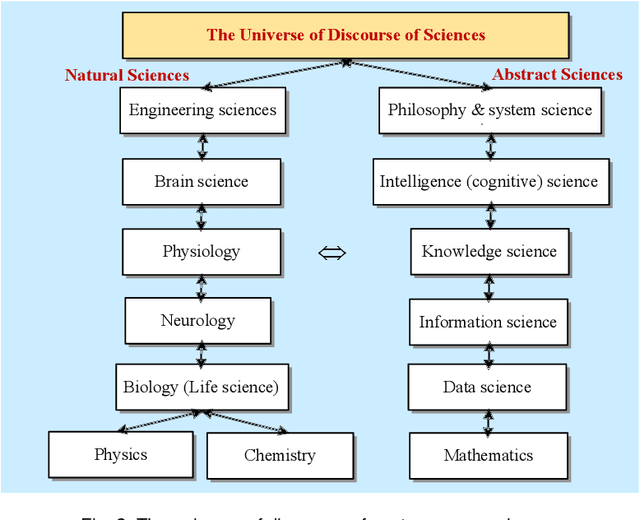
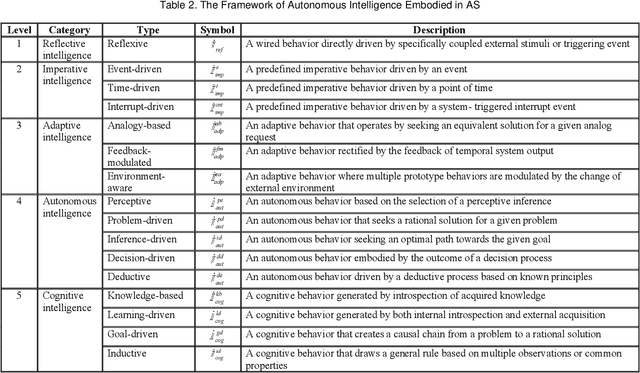
Symbiotic Autonomous Systems (SAS) are advanced intelligent and cognitive systems exhibiting autonomous collective intelligence enabled by coherent symbiosis of human-machine interactions in hybrid societies. Basic research in the emerging field of SAS has triggered advanced general AI technologies functioning without human intervention or hybrid symbiotic systems synergizing humans and intelligent machines into coherent cognitive systems. This work presents a theoretical framework of SAS underpinned by the latest advances in intelligence, cognition, computer, and system sciences. SAS are characterized by the composition of autonomous and symbiotic systems that adopt bio-brain-social-inspired and heterogeneously synergized structures and autonomous behaviors. This paper explores their cognitive and mathematical foundations. The challenge to seamless human-machine interactions in a hybrid environment is addressed. SAS-based collective intelligence is explored in order to augment human capability by autonomous machine intelligence towards the next generation of general AI, autonomous computers, and trustworthy mission-critical intelligent systems. Emerging paradigms and engineering applications of SAS are elaborated via an autonomous knowledge learning system that symbiotically works between humans and cognitive robots.

Magnification Generalization for Histopathology Image Embedding

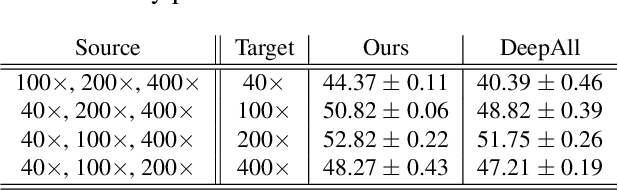
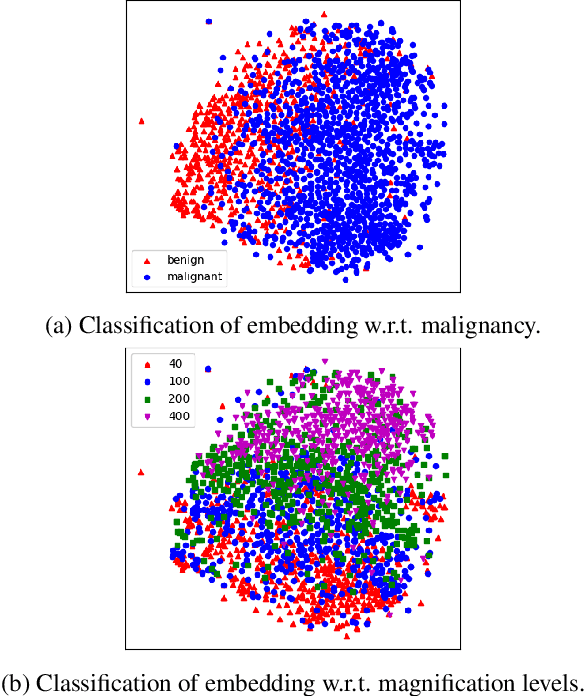
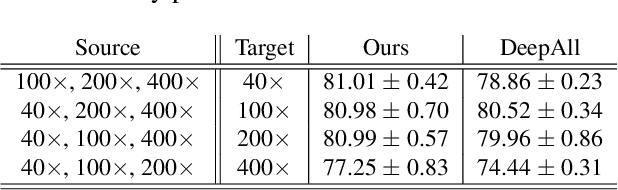
Histopathology image embedding is an active research area in computer vision. Most of the embedding models exclusively concentrate on a specific magnification level. However, a useful task in histopathology embedding is to train an embedding space regardless of the magnification level. Two main approaches for tackling this goal are domain adaptation and domain generalization, where the target magnification levels may or may not be introduced to the model in training, respectively. Although magnification adaptation is a well-studied topic in the literature, this paper, to the best of our knowledge, is the first work on magnification generalization for histopathology image embedding. We use an episodic trainable domain generalization technique for magnification generalization, namely Model Agnostic Learning of Semantic Features (MASF), which works based on the Model Agnostic Meta-Learning (MAML) concept. Our experimental results on a breast cancer histopathology dataset with four different magnification levels show the proposed method's effectiveness for magnification generalization.

Factor Analysis, Probabilistic Principal Component Analysis, Variational Inference, and Variational Autoencoder: Tutorial and Survey

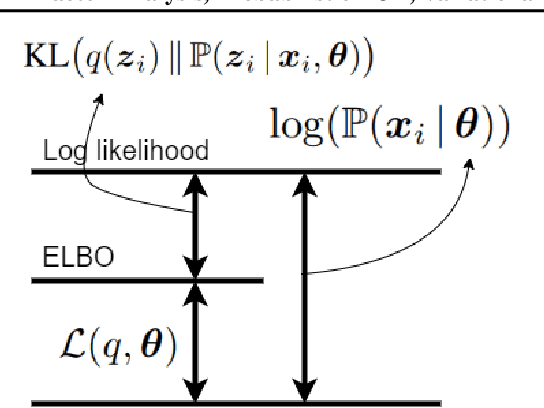
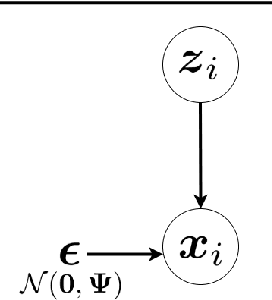
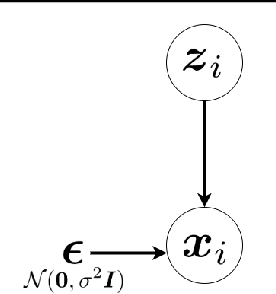
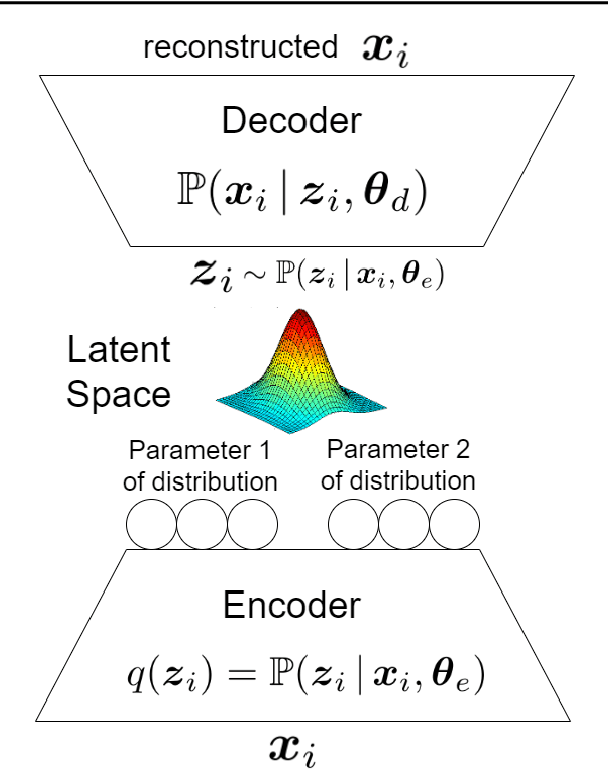
This is a tutorial and survey paper on factor analysis, probabilistic Principal Component Analysis (PCA), variational inference, and Variational Autoencoder (VAE). These methods, which are tightly related, are dimensionality reduction and generative models. They asssume that every data point is generated from or caused by a low-dimensional latent factor. By learning the parameters of distribution of latent space, the corresponding low-dimensional factors are found for the sake of dimensionality reduction. For their stochastic and generative behaviour, these models can also be used for generation of new data points in the data space. In this paper, we first start with variational inference where we derive the Evidence Lower Bound (ELBO) and Expectation Maximization (EM) for learning the parameters. Then, we introduce factor analysis, derive its joint and marginal distributions, and work out its EM steps. Probabilistic PCA is then explained, as a special case of factor analysis, and its closed-form solutions are derived. Finally, VAE is explained where the encoder, decoder and sampling from the latent space are introduced. Training VAE using both EM and backpropagation are explained.

Locally Linear Embedding and its Variants: Tutorial and Survey

This is a tutorial and survey paper for Locally Linear Embedding (LLE) and its variants. The idea of LLE is fitting the local structure of manifold in the embedding space. In this paper, we first cover LLE, kernel LLE, inverse LLE, and feature fusion with LLE. Then, we cover out-of-sample embedding using linear reconstruction, eigenfunctions, and kernel mapping. Incremental LLE is explained for embedding streaming data. Landmark LLE methods using the Nystrom approximation and locally linear landmarks are explained for big data embedding. We introduce the methods for parameter selection of number of neighbors using residual variance, Procrustes statistics, preservation neighborhood error, and local neighborhood selection. Afterwards, Supervised LLE (SLLE), enhanced SLLE, SLLE projection, probabilistic SLLE, supervised guided LLE (using Hilbert-Schmidt independence criterion), and semi-supervised LLE are explained for supervised and semi-supervised embedding. Robust LLE methods using least squares problem and penalty functions are also introduced for embedding in the presence of outliers and noise. Then, we introduce fusion of LLE with other manifold learning methods including Isomap (i.e., ISOLLE), principal component analysis, Fisher discriminant analysis, discriminant LLE, and Isotop. Finally, we explain weighted LLE in which the distances, reconstruction weights, or the embeddings are adjusted for better embedding; we cover weighted LLE for deformed distributed data, weighted LLE using probability of occurrence, SLLE by adjusting weights, modified LLE, and iterative LLE.

Sampling Algorithms, from Survey Sampling to Monte Carlo Methods: Tutorial and Literature Review

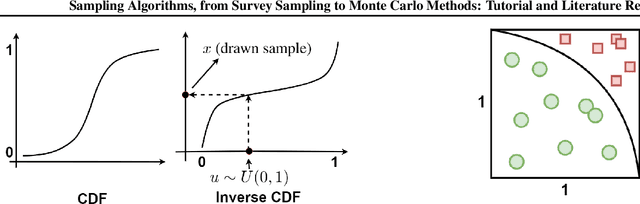
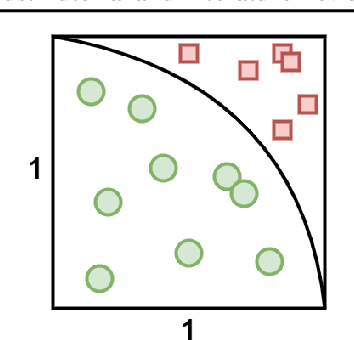
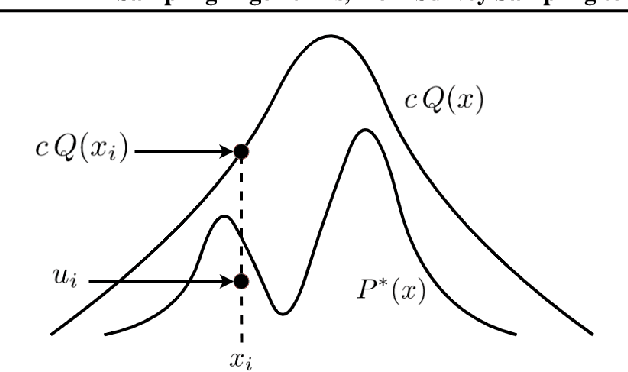
This paper is a tutorial and literature review on sampling algorithms. We have two main types of sampling in statistics. The first type is survey sampling which draws samples from a set or population. The second type is sampling from probability distribution where we have a probability density or mass function. In this paper, we cover both types of sampling. First, we review some required background on mean squared error, variance, bias, maximum likelihood estimation, Bernoulli, Binomial, and Hypergeometric distributions, the Horvitz-Thompson estimator, and the Markov property. Then, we explain the theory of simple random sampling, bootstrapping, stratified sampling, and cluster sampling. We also briefly introduce multistage sampling, network sampling, and snowball sampling. Afterwards, we switch to sampling from distribution. We explain sampling from cumulative distribution function, Monte Carlo approximation, simple Monte Carlo methods, and Markov Chain Monte Carlo (MCMC) methods. For simple Monte Carlo methods, whose iterations are independent, we cover importance sampling and rejection sampling. For MCMC methods, we cover Metropolis algorithm, Metropolis-Hastings algorithm, Gibbs sampling, and slice sampling. Then, we explain the random walk behaviour of Monte Carlo methods and more efficient Monte Carlo methods, including Hamiltonian (or hybrid) Monte Carlo, Adler's overrelaxation, and ordered overrelaxation. Finally, we summarize the characteristics, pros, and cons of sampling methods compared to each other. This paper can be useful for different fields of statistics, machine learning, reinforcement learning, and computational physics.