An Optimal Cascade Feature-Level Spatiotemporal Fusion Strategy for Anomaly Detection in CAN Bus

Autonomous vehicles represent a revolutionary advancement driven by the integration of artificial intelligence within intelligent transportation systems. However, they remain vulnerable due to the absence of robust security mechanisms in the Controller Area Network (CAN) bus. In order to mitigate the security issue, many machine learning models and strategies have been proposed, which primarily focus on a subset of dominant patterns of anomalies and lack rigorous evaluation in terms of reliability and robustness. Therefore, to address the limitations of previous works and mitigate the security vulnerability in CAN bus, the current study develops a model based on the intrinsic nature of the problem to cover all dominant patterns of anomalies. To achieve this, a cascade feature-level fusion strategy optimized by a two-parameter genetic algorithm is proposed to combine temporal and spatial information. Subsequently, the model is evaluated using a paired t-test to ensure reliability and robustness. Finally, a comprehensive comparative analysis conducted on two widely used datasets advocates that the proposed model outperforms other models and achieves superior accuracy and F1-score, demonstrating the best performance among all models presented to date.

Self-Supervised Learning Using Nonlinear Dependence

Self-supervised learning has gained significant attention in contemporary applications, particularly due to the scarcity of labeled data. While existing SSL methodologies primarily address feature variance and linear correlations, they often neglect the intricate relations between samples and the nonlinear dependencies inherent in complex data. In this paper, we introduce Correlation-Dependence Self-Supervised Learning (CDSSL), a novel framework that unifies and extends existing SSL paradigms by integrating both linear correlations and nonlinear dependencies, encapsulating sample-wise and feature-wise interactions. Our approach incorporates the Hilbert-Schmidt Independence Criterion (HSIC) to robustly capture nonlinear dependencies within a Reproducing Kernel Hilbert Space, enriching representation learning. Experimental evaluations on diverse benchmarks demonstrate the efficacy of CDSSL in improving representation quality.

Probabilistic Classification by Density Estimation Using Gaussian Mixture Model and Masked Autoregressive Flow

Density estimation, which estimates the distribution of data, is an important category of probabilistic machine learning. A family of density estimators is mixture models, such as Gaussian Mixture Model (GMM) by expectation maximization. Another family of density estimators is the generative models which generate data from input latent variables. One of the generative models is the Masked Autoregressive Flow (MAF) which makes use of normalizing flows and autoregressive networks. In this paper, we use the density estimators for classification, although they are often used for estimating the distribution of data. We model the likelihood of classes of data by density estimation, specifically using GMM and MAF. The proposed classifiers outperform simpler classifiers such as linear discriminant analysis which model the likelihood using only a single Gaussian distribution. This work opens the research door for proposing other probabilistic classifiers based on joint density estimation.

On Philomatics and Psychomatics for Combining Philosophy and Psychology with Mathematics

We propose the concepts of philomatics and psychomatics as hybrid combinations of philosophy and psychology with mathematics. We explain four motivations for this combination which are fulfilling the desire of analytical philosophy, proposing science of philosophy, justifying mathematical algorithms by philosophy, and abstraction in both philosophy and mathematics. We enumerate various examples for philomatics and psychomatics, some of which are explained in more depth. The first example is the analysis of relation between the context principle, semantic holism, and the usage theory of meaning with the attention mechanism in mathematics. The other example is on the relations of Plato's theory of forms in philosophy with the holographic principle in string theory, object-oriented programming, and machine learning. Finally, the relation between Wittgenstein's family resemblance and clustering in mathematics is explained. This paper opens the door of research for combining philosophy and psychology with mathematics.

Recurrent Neural Networks and Long Short-Term Memory Networks: Tutorial and Survey

This is a tutorial paper on Recurrent Neural Network (RNN), Long Short-Term Memory Network (LSTM), and their variants. We start with a dynamical system and backpropagation through time for RNN. Then, we discuss the problems of gradient vanishing and explosion in long-term dependencies. We explain close-to-identity weight matrix, long delays, leaky units, and echo state networks for solving this problem. Then, we introduce LSTM gates and cells, history and variants of LSTM, and Gated Recurrent Units (GRU). Finally, we introduce bidirectional RNN, bidirectional LSTM, and the Embeddings from Language Model (ELMo) network, for processing a sequence in both directions.

Gravitational Dimensionality Reduction Using Newtonian Gravity and Einstein's General Relativity

Due to the effectiveness of using machine learning in physics, it has been widely received increased attention in the literature. However, the notion of applying physics in machine learning has not been given much awareness to. This work is a hybrid of physics and machine learning where concepts of physics are used in machine learning. We propose the supervised Gravitational Dimensionality Reduction (GDR) algorithm where the data points of every class are moved to each other for reduction of intra-class variances and better separation of classes. For every data point, the other points are considered to be gravitational particles, such as stars, where the point is attracted to the points of its class by gravity. The data points are first projected onto a spacetime manifold using principal component analysis. We propose two variants of GDR -- one with the Newtonian gravity and one with the Einstein's general relativity. The former uses Newtonian gravity in a straight line between points but the latter moves data points along the geodesics of spacetime manifold. For GDR with relativity gravitation, we use both Schwarzschild and Minkowski metric tensors to cover both general relativity and special relativity. Our simulations show the effectiveness of GDR in discrimination of classes.

Affective Manifolds: Modeling Machine's Mind to Like, Dislike, Enjoy, Suffer, Worry, Fear, and Feel Like A Human

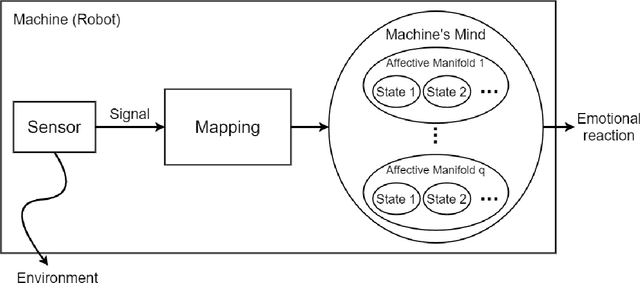
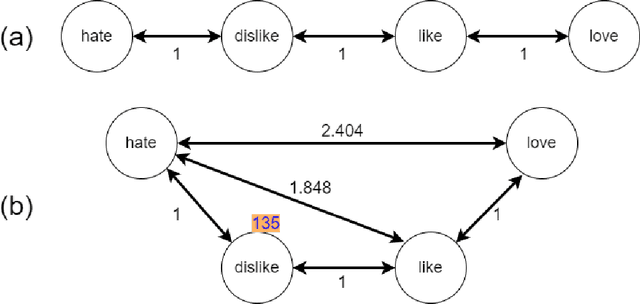
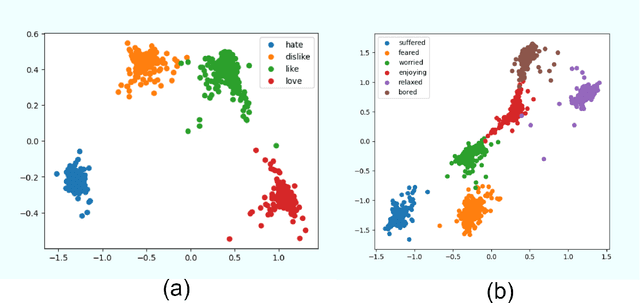
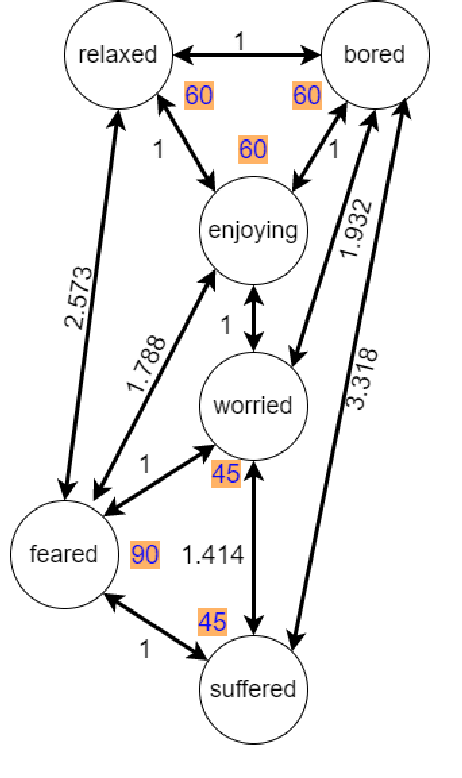
After the development of different machine learning and manifold learning algorithms, it may be a good time to put them together to make a powerful mind for machine. In this work, we propose affective manifolds as components of a machine's mind. Every affective manifold models a characteristic group of mind and contains multiple states. We define the machine's mind as a set of affective manifolds. We use a learning model for mapping the input signals to the embedding space of affective manifold. Using this mapping, a machine or a robot takes an input signal and can react emotionally to it. We use deep metric learning, with Siamese network, and propose a loss function for affective manifold learning. We define margins between states based on the psychological and philosophical studies. Using triplets of instances, we train the network to minimize the variance of every state and have the desired distances between states. We show that affective manifolds can have various applications for machine-machine and human-machine interactions. Some simulations are also provided for verification of the proposed method. It is possible to have as many affective manifolds as required in machine's mind. More affective manifolds in the machine's mind can make it more realistic and effective. This paper opens the door; we invite the researchers from various fields of science to propose more affective manifolds to be inserted in machine's mind.

Theoretical Connection between Locally Linear Embedding, Factor Analysis, and Probabilistic PCA

Locally Linear Embedding (LLE) is a nonlinear spectral dimensionality reduction and manifold learning method. It has two main steps which are linear reconstruction and linear embedding of points in the input space and embedding space, respectively. In this work, we look at the linear reconstruction step from a stochastic perspective where it is assumed that every data point is conditioned on its linear reconstruction weights as latent factors. The stochastic linear reconstruction of LLE is solved using expectation maximization. We show that there is a theoretical connection between three fundamental dimensionality reduction methods, i.e., LLE, factor analysis, and probabilistic Principal Component Analysis (PCA). The stochastic linear reconstruction of LLE is formulated similar to the factor analysis and probabilistic PCA. It is also explained why factor analysis and probabilistic PCA are linear and LLE is a nonlinear method. This work combines and makes a bridge between two broad approaches of dimensionality reduction, i.e., the spectral and probabilistic algorithms.

On Manifold Hypothesis: Hypersurface Submanifold Embedding Using Osculating Hyperspheres

Consider a set of $n$ data points in the Euclidean space $\mathbb{R}^d$. This set is called dataset in machine learning and data science. Manifold hypothesis states that the dataset lies on a low-dimensional submanifold with high probability. All dimensionality reduction and manifold learning methods have the assumption of manifold hypothesis. In this paper, we show that the dataset lies on an embedded hypersurface submanifold which is locally $(d-1)$-dimensional. Hence, we show that the manifold hypothesis holds at least for the embedding dimensionality $d-1$. Using an induction in a pyramid structure, we also extend the embedding dimensionality to lower embedding dimensionalities to show the validity of manifold hypothesis for embedding dimensionalities $\{1, 2, \dots, d-1\}$. For embedding the hypersurface, we first construct the $d$ nearest neighbors graph for data. For every point, we fit an osculating hypersphere $S^{d-1}$ using its neighbors where this hypersphere is osculating to a hypothetical hypersurface. Then, using surgery theory, we apply surgery on the osculating hyperspheres to obtain $n$ hyper-caps. We connect the hyper-caps to one another using partial hyper-cylinders. By connecting all parts, the embedded hypersurface is obtained as the disjoint union of these elements. We discuss the geometrical characteristics of the embedded hypersurface, such as having boundary, its topology, smoothness, boundedness, orientability, compactness, and injectivity. Some discussion are also provided for the linearity and structure of data. This paper is the intersection of several fields of science including machine learning, differential geometry, and algebraic topology.

Spectral, Probabilistic, and Deep Metric Learning: Tutorial and Survey

This is a tutorial and survey paper on metric learning. Algorithms are divided into spectral, probabilistic, and deep metric learning. We first start with the definition of distance metric, Mahalanobis distance, and generalized Mahalanobis distance. In spectral methods, we start with methods using scatters of data, including the first spectral metric learning, relevant methods to Fisher discriminant analysis, Relevant Component Analysis (RCA), Discriminant Component Analysis (DCA), and the Fisher-HSIC method. Then, large-margin metric learning, imbalanced metric learning, locally linear metric adaptation, and adversarial metric learning are covered. We also explain several kernel spectral methods for metric learning in the feature space. We also introduce geometric metric learning methods on the Riemannian manifolds. In probabilistic methods, we start with collapsing classes in both input and feature spaces and then explain the neighborhood component analysis methods, Bayesian metric learning, information theoretic methods, and empirical risk minimization in metric learning. In deep learning methods, we first introduce reconstruction autoencoders and supervised loss functions for metric learning. Then, Siamese networks and its various loss functions, triplet mining, and triplet sampling are explained. Deep discriminant analysis methods, based on Fisher discriminant analysis, are also reviewed. Finally, we introduce multi-modal deep metric learning, geometric metric learning by neural networks, and few-shot metric learning.