Approaching Rate-Distortion Limits in Neural Compression with Lattice Transform Coding

Neural compression has brought tremendous progress in designing lossy compressors with good rate-distortion (RD) performance at low complexity. Thus far, neural compression design involves transforming the source to a latent vector, which is then rounded to integers and entropy coded. While this approach has been shown to be optimal in a one-shot sense on certain sources, we show that it is highly sub-optimal on i.i.d. sequences, and in fact always recovers scalar quantization of the original source sequence. We demonstrate that the sub-optimality is due to the choice of quantization scheme in the latent space, and not the transform design. By employing lattice quantization instead of scalar quantization in the latent space, we demonstrate that Lattice Transform Coding (LTC) is able to recover optimal vector quantization at various dimensions and approach the asymptotically-achievable rate-distortion function at reasonable complexity. On general vector sources, LTC improves upon standard neural compressors in one-shot coding performance. LTC also enables neural compressors that perform block coding on i.i.d. vector sources, which yields coding gain over optimal one-shot coding.

Score-Based Methods for Discrete Optimization in Deep Learning

Discrete optimization problems often arise in deep learning tasks, despite the fact that neural networks typically operate on continuous data. One class of these problems involve objective functions which depend on neural networks, but optimization variables which are discrete. Although the discrete optimization literature provides efficient algorithms, they are still impractical in these settings due to the high cost of an objective function evaluation, which involves a neural network forward-pass. In particular, they require $O(n)$ complexity per iteration, but real data such as point clouds have values of $n$ in thousands or more. In this paper, we investigate a score-based approximation framework to solve such problems. This framework uses a score function as a proxy for the marginal gain of the objective, leveraging embeddings of the discrete variables and speed of auto-differentiation frameworks to compute backward-passes in parallel. We experimentally demonstrate, in adversarial set classification tasks, that our method achieves a superior trade-off in terms of speed and solution quality compared to heuristic methods.

WrappingNet: Mesh Autoencoder via Deep Sphere Deformation

There have been recent efforts to learn more meaningful representations via fixed length codewords from mesh data, since a mesh serves as a complete model of underlying 3D shape compared to a point cloud. However, the mesh connectivity presents new difficulties when constructing a deep learning pipeline for meshes. Previous mesh unsupervised learning approaches typically assume category-specific templates, e.g., human face/body templates. It restricts the learned latent codes to only be meaningful for objects in a specific category, so the learned latent spaces are unable to be used across different types of objects. In this work, we present WrappingNet, the first mesh autoencoder enabling general mesh unsupervised learning over heterogeneous objects. It introduces a novel base graph in the bottleneck dedicated to representing mesh connectivity, which is shown to facilitate learning a shared latent space representing object shape. The superiority of WrappingNet mesh learning is further demonstrated via improved reconstruction quality and competitive classification compared to point cloud learning, as well as latent interpolation between meshes of different categories.

Text + Sketch: Image Compression at Ultra Low Rates

Recent advances in text-to-image generative models provide the ability to generate high-quality images from short text descriptions. These foundation models, when pre-trained on billion-scale datasets, are effective for various downstream tasks with little or no further training. A natural question to ask is how such models may be adapted for image compression. We investigate several techniques in which the pre-trained models can be directly used to implement compression schemes targeting novel low rate regimes. We show how text descriptions can be used in conjunction with side information to generate high-fidelity reconstructions that preserve both semantics and spatial structure of the original. We demonstrate that at very low bit-rates, our method can significantly improve upon learned compressors in terms of perceptual and semantic fidelity, despite no end-to-end training.

On a Relation Between the Rate-Distortion Function and Optimal Transport

We discuss a relationship between rate-distortion and optimal transport (OT) theory, even though they seem to be unrelated at first glance. In particular, we show that a function defined via an extremal entropic OT distance is equivalent to the rate-distortion function. We numerically verify this result as well as previous results that connect the Monge and Kantorovich problems to optimal scalar quantization. Thus, we unify solving scalar quantization and rate-distortion functions in an alternative fashion by using their respective optimal transport solvers.

Federated Neural Compression Under Heterogeneous Data

We discuss a federated learned compression problem, where the goal is to learn a compressor from real-world data which is scattered across clients and may be statistically heterogeneous, yet share a common underlying representation. We propose a distributed source model that encompasses both characteristics, and naturally suggests a compressor architecture that uses analysis and synthesis transforms shared by clients. Inspired by personalized federated learning methods, we employ an entropy model that is personalized to each client. This allows for a global latent space to be learned across clients, and personalized entropy models that adapt to the clients' latent distributions. We show empirically that this strategy outperforms solely local methods, which indicates that learned compression also benefits from a shared global representation in statistically heterogeneous federated settings.

Neural Estimation of the Rate-Distortion Function With Applications to Operational Source Coding

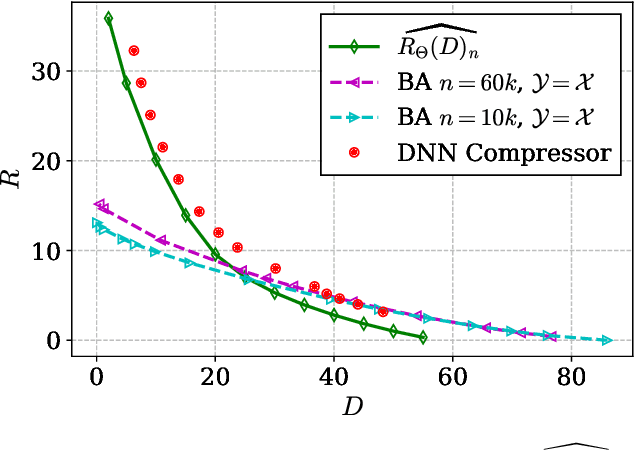
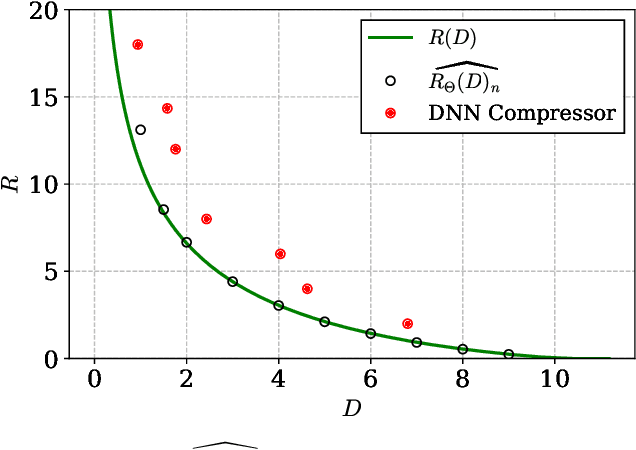
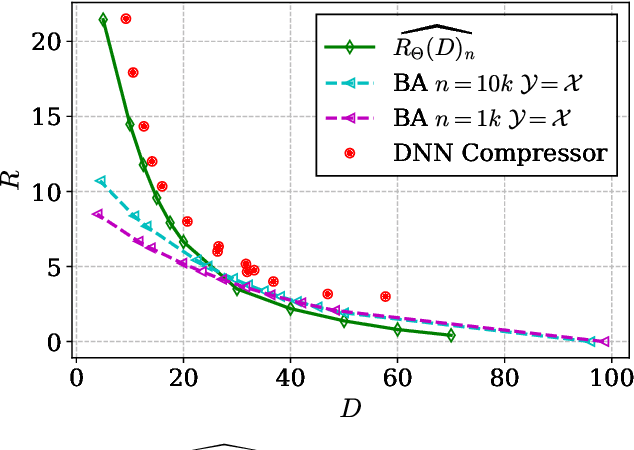
A fundamental question in designing lossy data compression schemes is how well one can do in comparison with the rate-distortion function, which describes the known theoretical limits of lossy compression. Motivated by the empirical success of deep neural network (DNN) compressors on large, real-world data, we investigate methods to estimate the rate-distortion function on such data, which would allow comparison of DNN compressors with optimality. While one could use the empirical distribution of the data and apply the Blahut-Arimoto algorithm, this approach presents several computational challenges and inaccuracies when the datasets are large and high-dimensional, such as the case of modern image datasets. Instead, we re-formulate the rate-distortion objective, and solve the resulting functional optimization problem using neural networks. We apply the resulting rate-distortion estimator, called NERD, on popular image datasets, and provide evidence that NERD can accurately estimate the rate-distortion function. Using our estimate, we show that the rate-distortion achievable by DNN compressors are within several bits of the rate-distortion function for real-world datasets. Additionally, NERD provides access to the rate-distortion achieving channel, as well as samples from its output marginal. Therefore, using recent results in reverse channel coding, we describe how NERD can be used to construct an operational one-shot lossy compression scheme with guarantees on the achievable rate and distortion. Experimental results demonstrate competitive performance with DNN compressors.

Robust Graph Neural Networks via Probabilistic Lipschitz Constraints

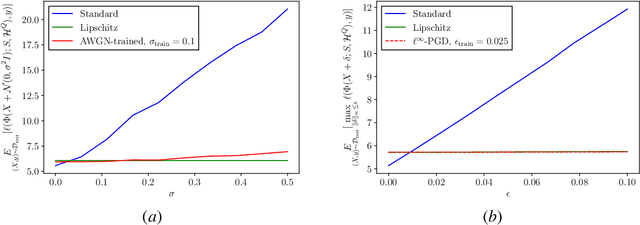
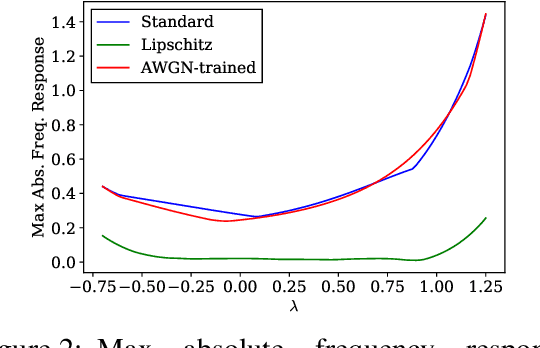
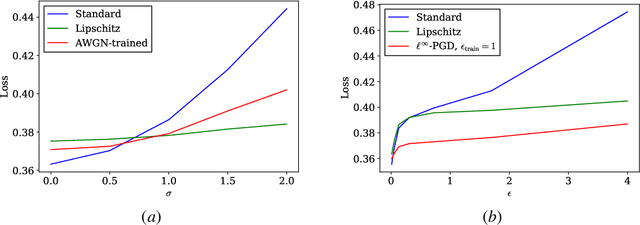
Graph neural networks (GNNs) have recently been demonstrated to perform well on a variety of network-based tasks such as decentralized control and resource allocation, and provide computationally efficient methods for these tasks which have traditionally been challenging in that regard. However, like many neural-network based systems, GNNs are susceptible to shifts and perturbations on their inputs, which can include both node attributes and graph structure. In order to make them more useful for real-world applications, it is important to ensure their robustness post-deployment. Motivated by controlling the Lipschitz constant of GNN filters with respect to the node attributes, we propose to constrain the frequency response of the GNN's filter banks. We extend this formulation to the dynamic graph setting using a continuous frequency response constraint, and solve a relaxed variant of the problem via the scenario approach. This allows for the use of the same computationally efficient algorithm on sampled constraints, which provides PAC-style guarantees on the stability of the GNN using results in scenario optimization. We also highlight an important connection between this setup and GNN stability to graph perturbations, and provide experimental results which demonstrate the efficacy and broadness of our approach.

Out-of-Distribution Robustness in Deep Learning Compression

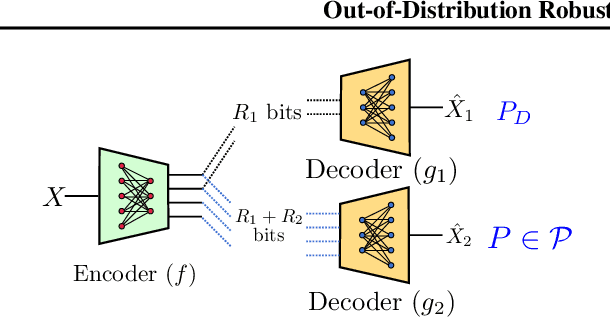
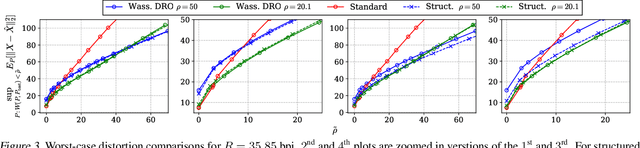
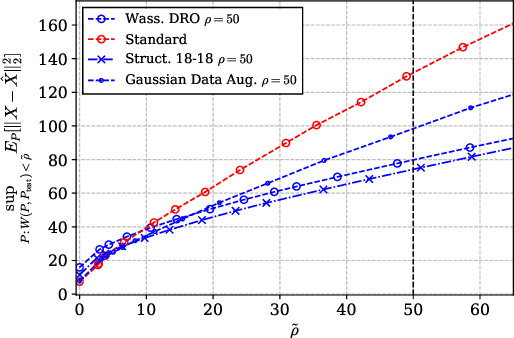
In recent years, deep neural network (DNN) compression systems have proved to be highly effective for designing source codes for many natural sources. However, like many other machine learning systems, these compressors suffer from vulnerabilities to distribution shifts as well as out-of-distribution (OOD) data, which reduces their real-world applications. In this paper, we initiate the study of OOD robust compression. Considering robustness to two types of ambiguity sets (Wasserstein balls and group shifts), we propose algorithmic and architectural frameworks built on two principled methods: one that trains DNN compressors using distributionally-robust optimization (DRO), and the other which uses a structured latent code. Our results demonstrate that both methods enforce robustness compared to a standard DNN compressor, and that using a structured code can be superior to the DRO compressor. We observe tradeoffs between robustness and distortion and corroborate these findings theoretically for a specific class of sources.

Siamese Neural Networks for Wireless Positioning and Channel Charting

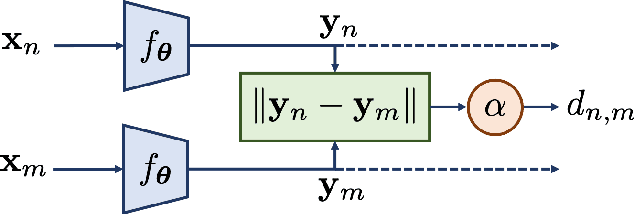
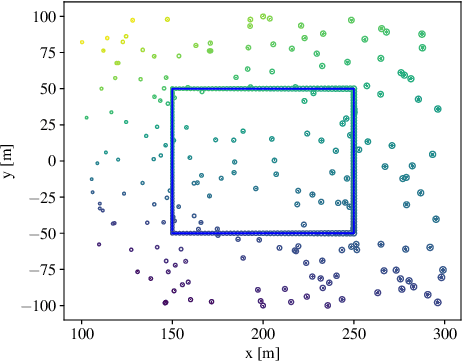
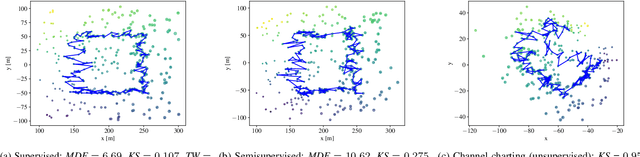
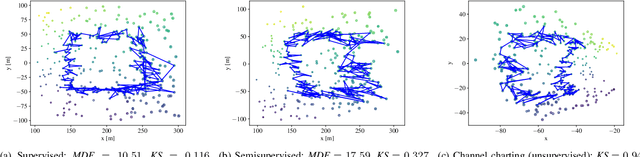
Neural networks have been proposed recently for positioning and channel charting of user equipments (UEs) in wireless systems. Both of these approaches process channel state information (CSI) that is acquired at a multi-antenna base-station in order to learn a function that maps CSI to location information. CSI-based positioning using deep neural networks requires a dataset that contains both CSI and associated location information. Channel charting (CC) only requires CSI information to extract relative position information. Since CC builds on dimensionality reduction, it can be implemented using autoencoders. In this paper, we propose a unified architecture based on Siamese networks that can be used for supervised UE positioning and unsupervised channel charting. In addition, our framework enables semisupervised positioning, where only a small set of location information is available during training. We use simulations to demonstrate that Siamese networks achieve similar or better performance than existing positioning and CC approaches with a single, unified neural network architecture.