A Behavioural and Representational Evaluation of Goal-Directedness in Language Model Agents

Understanding an agent's goals helps explain and predict its behaviour, yet there is no established methodology for reliably attributing goals to agentic systems. We propose a framework for evaluating goal-directedness that integrates behavioural evaluation with interpretability-based analyses of models' internal representations. As a case study, we examine an LLM agent navigating a 2D grid world toward a goal state. Behaviourally, we evaluate the agent against an optimal policy across varying grid sizes, obstacle densities, and goal structures, finding that performance scales with task difficulty while remaining robust to difficulty-preserving transformations and complex goal structures. We then use probing methods to decode the agent's internal representations of the environment state and its multi-step action plans. We find that the LLM agent non-linearly encodes a coarse spatial map of the environment, preserving approximate task-relevant cues about its position and the goal location; that its actions are broadly consistent with these internal representations; and that reasoning reorganises them, shifting from broader environment structural cues toward information supporting immediate action selection. Our findings support the view that introspective examination is required beyond behavioural evaluations to characterise how agents represent and pursue their objectives.

Robust Graph Neural Networks via Probabilistic Lipschitz Constraints

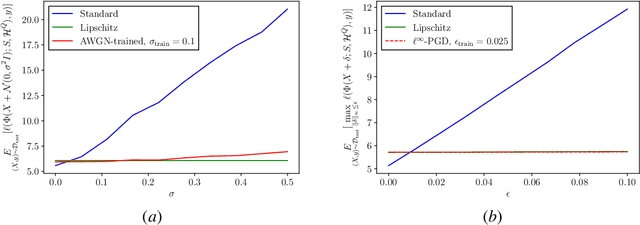
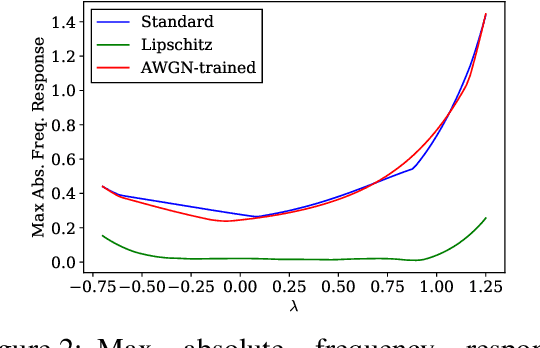
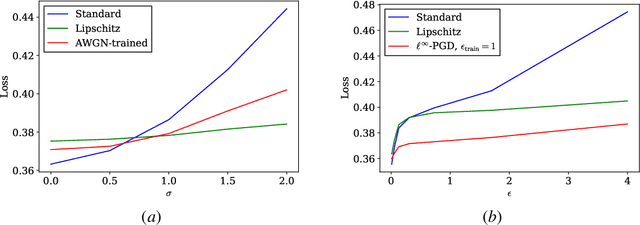
Graph neural networks (GNNs) have recently been demonstrated to perform well on a variety of network-based tasks such as decentralized control and resource allocation, and provide computationally efficient methods for these tasks which have traditionally been challenging in that regard. However, like many neural-network based systems, GNNs are susceptible to shifts and perturbations on their inputs, which can include both node attributes and graph structure. In order to make them more useful for real-world applications, it is important to ensure their robustness post-deployment. Motivated by controlling the Lipschitz constant of GNN filters with respect to the node attributes, we propose to constrain the frequency response of the GNN's filter banks. We extend this formulation to the dynamic graph setting using a continuous frequency response constraint, and solve a relaxed variant of the problem via the scenario approach. This allows for the use of the same computationally efficient algorithm on sampled constraints, which provides PAC-style guarantees on the stability of the GNN using results in scenario optimization. We also highlight an important connection between this setup and GNN stability to graph perturbations, and provide experimental results which demonstrate the efficacy and broadness of our approach.