Towards Reproducible Learning-based Compression

A deep learning system typically suffers from a lack of reproducibility that is partially rooted in hardware or software implementation details. The irreproducibility leads to skepticism in deep learning technologies and it can hinder them from being deployed in many applications. In this work, the irreproducibility issue is analyzed where deep learning is employed in compression systems while the encoding and decoding may be run on devices from different manufacturers. The decoding process can even crash due to a single bit difference, e.g., in a learning-based entropy coder. For a given deep learning-based module with limited resources for protection, we first suggest that reproducibility can only be assured when the mismatches are bounded. Then a safeguarding mechanism is proposed to tackle the challenges. The proposed method may be applied for different levels of protection either at the reconstruction level or at a selected decoding level. Furthermore, the overhead introduced for the protection can be scaled down accordingly when the error bound is being suppressed. Experiments demonstrate the effectiveness of the proposed approach for learning-based compression systems, e.g., in image compression and point cloud compression.

WrappingNet: Mesh Autoencoder via Deep Sphere Deformation

There have been recent efforts to learn more meaningful representations via fixed length codewords from mesh data, since a mesh serves as a complete model of underlying 3D shape compared to a point cloud. However, the mesh connectivity presents new difficulties when constructing a deep learning pipeline for meshes. Previous mesh unsupervised learning approaches typically assume category-specific templates, e.g., human face/body templates. It restricts the learned latent codes to only be meaningful for objects in a specific category, so the learned latent spaces are unable to be used across different types of objects. In this work, we present WrappingNet, the first mesh autoencoder enabling general mesh unsupervised learning over heterogeneous objects. It introduces a novel base graph in the bottleneck dedicated to representing mesh connectivity, which is shown to facilitate learning a shared latent space representing object shape. The superiority of WrappingNet mesh learning is further demonstrated via improved reconstruction quality and competitive classification compared to point cloud learning, as well as latent interpolation between meshes of different categories.

GRASP-Net: Geometric Residual Analysis and Synthesis for Point Cloud Compression

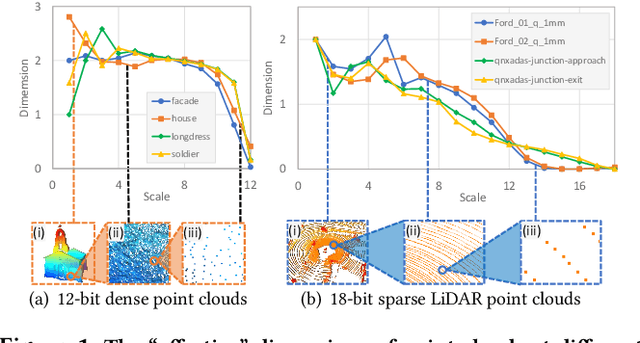
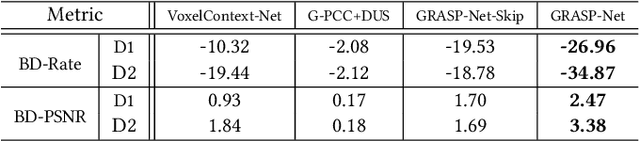
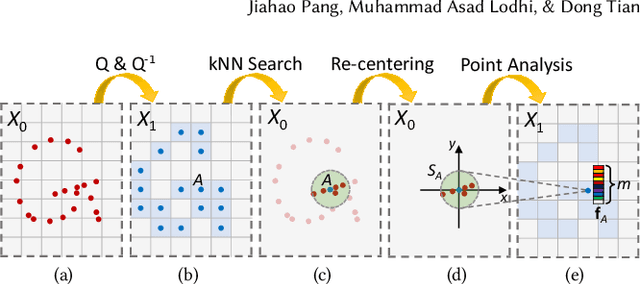
Point cloud compression (PCC) is a key enabler for various 3-D applications, owing to the universality of the point cloud format. Ideally, 3D point clouds endeavor to depict object/scene surfaces that are continuous. Practically, as a set of discrete samples, point clouds are locally disconnected and sparsely distributed. This sparse nature is hindering the discovery of local correlation among points for compression. Motivated by an analysis with fractal dimension, we propose a heterogeneous approach with deep learning for lossy point cloud geometry compression. On top of a base layer compressing a coarse representation of the input, an enhancement layer is designed to cope with the challenging geometric residual/details. Specifically, a point-based network is applied to convert the erratic local details to latent features residing on the coarse point cloud. Then a sparse convolutional neural network operating on the coarse point cloud is launched. It utilizes the continuity/smoothness of the coarse geometry to compress the latent features as an enhancement bit-stream that greatly benefits the reconstruction quality. When this bit-stream is unavailable, e.g., due to packet loss, we support a skip mode with the same architecture which generates geometric details from the coarse point cloud directly. Experimentation on both dense and sparse point clouds demonstrate the state-of-the-art compression performance achieved by our proposal. Our code is available at https://github.com/InterDigitalInc/GRASP-Net.

Learning Product Graphs Underlying Smooth Graph Signals

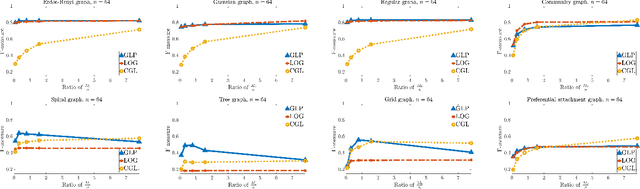
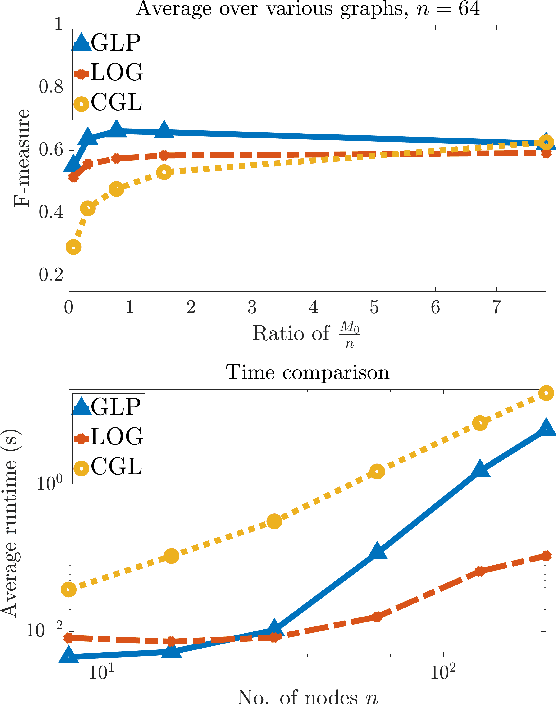
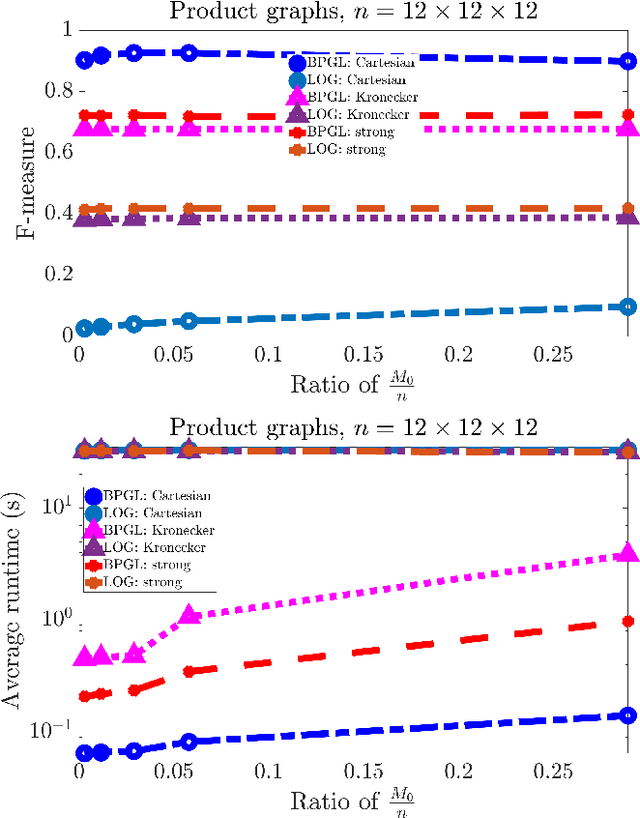
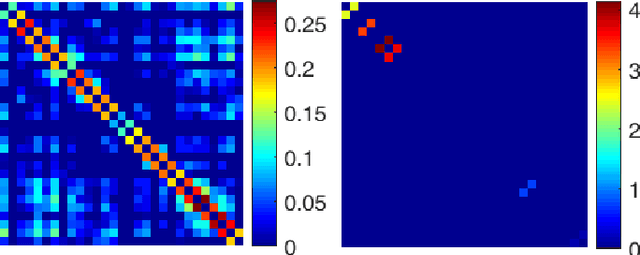
Real-world data is often times associated with irregular structures that can analytically be represented as graphs. Having access to this graph, which is sometimes trivially evident from domain knowledge, provides a better representation of the data and facilitates various information processing tasks. However, in cases where the underlying graph is unavailable, it needs to be learned from the data itself for data representation, data processing and inference purposes. Existing literature on learning graphs from data has mostly considered arbitrary graphs, whereas the graphs generating real-world data tend to have additional structure that can be incorporated in the graph learning procedure. Structure-aware graph learning methods require learning fewer parameters and have the potential to reduce computational, memory and sample complexities. In light of this, the focus of this paper is to devise a method to learn structured graphs from data that are given in the form of product graphs. Product graphs arise naturally in many real-world datasets and provide an efficient and compact representation of large-scale graphs through several smaller factor graphs. To this end, first the graph learning problem is posed as a linear program, which (on average) outperforms the state-of-the-art graph learning algorithms. This formulation is of independent interest itself as it shows that graph learning is possible through a simple linear program. Afterwards, an alternating minimization-based algorithm aimed at learning various types of product graphs is proposed, and local convergence guarantees to the true solution are established for this algorithm. Finally the performance gains, reduced sample complexity, and inference capabilities of the proposed algorithm over existing methods are also validated through numerical simulations on synthetic and real datasets.