HyColor: An Efficient Heuristic Algorithm for Graph Coloring

The graph coloring problem (GCP) is a classic combinatorial optimization problem that aims to find the minimum number of colors assigned to vertices of a graph such that no two adjacent vertices receive the same color. GCP has been extensively studied by researchers from various fields, including mathematics, computer science, and biological science. Due to the NP-hard nature, many heuristic algorithms have been proposed to solve GCP. However, existing GCP algorithms focus on either small hard graphs or large-scale sparse graphs (with up to 10^7 vertices). This paper presents an efficient hybrid heuristic algorithm for GCP, named HyColor, which excels in handling large-scale sparse graphs while achieving impressive results on small dense graphs. The efficiency of HyColor comes from the following three aspects: a local decision strategy to improve the lower bound on the chromatic number; a graph-reduction strategy to reduce the working graph; and a k-core and mixed degree-based greedy heuristic for efficiently coloring graphs. HyColor is evaluated against three state-of-the-art GCP algorithms across four benchmarks, comprising three large-scale sparse graph benchmarks and one small dense graph benchmark, totaling 209 instances. The results demonstrate that HyColor consistently outperforms existing heuristic algorithms in both solution accuracy and computational efficiency for the majority of instances. Notably, HyColor achieved the best solutions in 194 instances (over 93%), with 34 of these solutions significantly surpassing those of other algorithms. Furthermore, HyColor successfully determined the chromatic number and achieved optimal coloring in 128 instances.

Dynamic Location Search for Identifying Maximum Weighted Independent Sets in Complex Networks

While Artificial intelligence (AI), including Generative AI, are effective at generating high-quality traffic data and optimization solutions in intelligent transportation systems (ITSs), these techniques often demand significant training time and computational resources, especially in large-scale and complex scenarios. To address this, we introduce a novel and efficient algorithm for solving the maximum weighted independent set (MWIS) problem, which can be used to model many ITSs applications, such as traffic signal control and vehicle routing. Given the NP-hard nature of the MWIS problem, our proposed algorithm, DynLS, incorporates three key innovations to solve it effectively. First, it uses a scores-based adaptive vertex perturbation (SAVP) technique to accelerate convergence, particularly in sparse graphs. Second, it includes a region location mechanism (RLM) to help escape local optima by dynamically adjusting the search space. Finally, it employs a novel variable neighborhood descent strategy, ComLS, which combines vertex exchange strategies with a reward mechanism to guide the search toward high-quality solutions. Our experimental results demonstrate DynLS's superior performance, consistently delivering high-quality solutions within 1000 seconds. DynLS outperformed five leading algorithms across 360 test instances, achieving the best solution for 350 instances and surpassing the second-best algorithm, Cyclic-Fast, by 177 instances. Moreover, DynLS matched Cyclic-Fast's convergence speed, highlighting its efficiency and practicality. This research represents a significant advancement in heuristic algorithms for the MWIS problem, offering a promising approach to aid AI techniques in optimizing intelligent transportation systems.

Optimizing Minimum Vertex Cover Solving via a GCN-assisted Heuristic Algorithm

The problem of finding a minimum vertex cover (MVC) in a graph is a well-known NP-hard problem with significant practical applications in optimization and scheduling. Its complexity, combined with the increasing scale of problems, underscores the need for efficient and effective algorithms. However, existing heuristic algorithms for MVC often rely on simplistic initialization strategies and overlook the impact of edge attributes and neighborhood information on vertex selection. In this paper, we introduce GCNIVC, a novel heuristic search algorithm designed to address the limitations of existing methods for solving MVC problems in large-scale graphs. Our approach features two main innovations. First, it utilizes a Graph Convolutional Network (GCN) to capture the global structure of graphs, which enables the generation of high-quality initial solutions that enhance the efficiency of the subsequent search process. Second, GCNIVC introduces a new heuristic that employs three containers and the concept of double-covered edges (dc-edges), improving search efficiency and providing greater flexibility for adding and removing operations based on edge attributes. Through extensive experiments on benchmark datasets, we demonstrate that GCNIVC outperforms state-of-the-art MVC algorithms in terms of both accuracy and efficiency. Our results highlight the effectiveness of GCNIVC's GCN-assisted initialization and its edge-informed search strategy. This study not only advances the understanding of MVC problem-solving but also contributes a new tool for addressing large-scale graph optimization challenges.

Guiding Multi-agent Multi-task Reinforcement Learning by a Hierarchical Framework with Logical Reward Shaping

Multi-agent hierarchical reinforcement learning (MAHRL) has been studied as an effective means to solve intelligent decision problems in complex and large-scale environments. However, most current MAHRL algorithms follow the traditional way of using reward functions in reinforcement learning, which limits their use to a single task. This study aims to design a multi-agent cooperative algorithm with logic reward shaping (LRS), which uses a more flexible way of setting the rewards, allowing for the effective completion of multi-tasks. LRS uses Linear Temporal Logic (LTL) to express the internal logic relation of subtasks within a complex task. Then, it evaluates whether the subformulae of the LTL expressions are satisfied based on a designed reward structure. This helps agents to learn to effectively complete tasks by adhering to the LTL expressions, thus enhancing the interpretability and credibility of their decisions. To enhance coordination and cooperation among multiple agents, a value iteration technique is designed to evaluate the actions taken by each agent. Based on this evaluation, a reward function is shaped for coordination, which enables each agent to evaluate its status and complete the remaining subtasks through experiential learning. Experiments have been conducted on various types of tasks in the Minecraft-like environment. The results demonstrate that the proposed algorithm can improve the performance of multi-agents when learning to complete multi-tasks.

DFDRNN: A dual-feature based neural network for drug repositioning

Drug repositioning is an economically efficient strategy used to discover new indications for existing drugs beyond their original approvals, expanding their applicability and usage to address challenges in disease treatment. In recent years, deep-learning techniques for drug repositioning have gained much attention. While most deep learning-based research methods focus on encoding drugs and diseases by extracting feature information from neighbors in the network, they often pay little attention to the potential relationships between the features of drugs and diseases, leading to imprecise encoding of drugs and diseases. To address this, we design a dual-feature drug repositioning neural network (DFDRNN) model to achieve precise encoding of drugs and diseases. DFDRNN uses two features to represent drugs and diseases: the similarity feature and the association feature. The model incorporates a self-attention mechanism to design two dual-feature extraction modules for achieving precisely encoding of drugs and diseases: the intra-domain dual-feature extraction (IntraDDFE) module and the inter-domain dual-feature extraction (InterDDFE) module. The IntraDDFE module extracts features from a single domain (drug or disease domain), while the InterDDFE module extracts features from the mixed domain (drug and disease domain). In particular, the feature is changed by InterDDFE, ensuring a precise encoding of drugs and diseases. Finally, a cross-dual-domain decoder is designed to predict drug-disease associations in both the drug and disease domains. Compared to six state-of-the-art methods, DFDRNN outperforms others on four benchmark datasets, with an average AUROC of 0.946 and an average AUPR of 0.597.

Improving Critical Node Detection Using Neural Network-based Initialization in a Genetic Algorithm

The Critical Node Problem (CNP) is concerned with identifying the critical nodes in a complex network. These nodes play a significant role in maintaining the connectivity of the network, and removing them can negatively impact network performance. CNP has been studied extensively due to its numerous real-world applications. Among the different versions of CNP, CNP-1a has gained the most popularity. The primary objective of CNP-1a is to minimize the pair-wise connectivity in the remaining network after deleting a limited number of nodes from a network. Due to the NP-hard nature of CNP-1a, many heuristic/metaheuristic algorithms have been proposed to solve this problem. However, most existing algorithms start with a random initialization, leading to a high cost of obtaining an optimal solution. To improve the efficiency of solving CNP-1a, a knowledge-guided genetic algorithm named K2GA has been proposed. Unlike the standard genetic algorithm framework, K2GA has two main components: a pretrained neural network to obtain prior knowledge on possible critical nodes, and a hybrid genetic algorithm with local search for finding an optimal set of critical nodes based on the knowledge given by the trained neural network. The local search process utilizes a cut node-based greedy strategy. The effectiveness of the proposed knowledgeguided genetic algorithm is verified by experiments on 26 realworld instances of complex networks. Experimental results show that K2GA outperforms the state-of-the-art algorithms regarding the best, median, and average objective values, and improves the best upper bounds on the best objective values for eight realworld instances.

A Dual-mode Local Search Algorithm for Solving the Minimum Dominating Set Problem

Given a graph, the minimum dominating set (MinDS) problem is to identify a smallest set $D$ of vertices such that every vertex not in $D$ is adjacent to at least one vertex in $D$. The MinDS problem is a classic $\mathcal{NP}$-hard problem and has been extensively studied because of its many disparate applications in network analysis. To solve this problem efficiently, many heuristic approaches have been proposed to obtain a good solution within an acceptable time limit. However, existing MinDS heuristic algorithms are always limited by various tie-breaking cases when selecting vertices, which slows down the effectiveness of the algorithms. In this paper, we design an efficient local search algorithm for the MinDS problem, named DmDS -- a dual-mode local search framework that probabilistically chooses between two distinct vertex-swapping schemes. We further address limitations of other algorithms by introducing vertex selection criterion based on the frequency of vertices added to solutions to address tie-breaking cases, and a new strategy to improve the quality of the initial solution via a greedy-based strategy integrated with perturbation. We evaluate DmDS against the state-of-the-art algorithms on seven datasets, consisting of 346 instances (or families) with up to tens of millions of vertices. Experimental results show that DmDS obtains the best performance in accuracy for almost all instances and finds much better solutions than state-of-the-art MinDS algorithms on a broad range of large real-world graphs.

An Adaptive Repeated-Intersection-Reduction Local Search for the Maximum Independent Set Problem

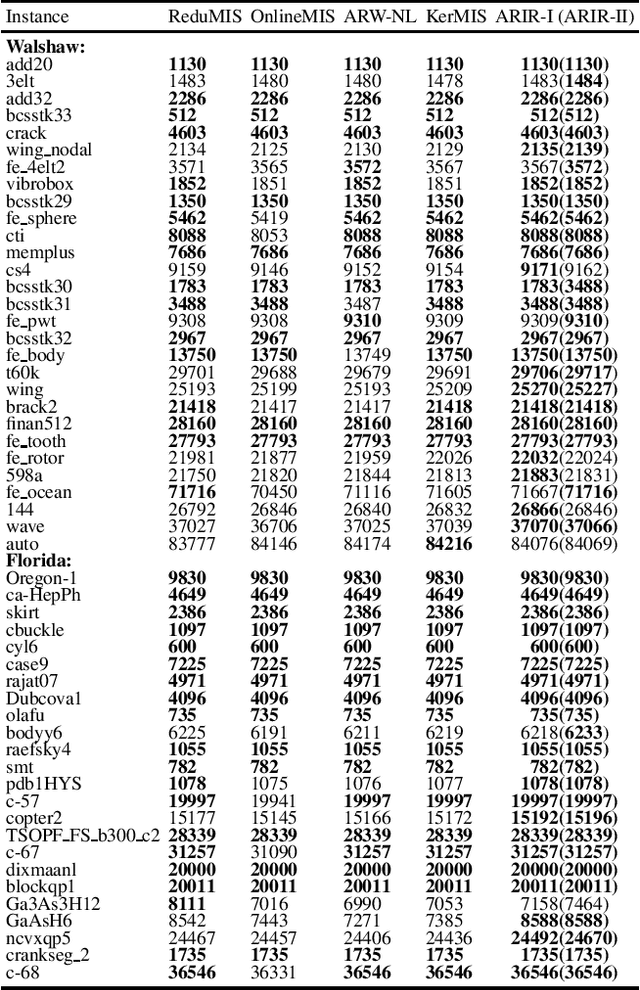
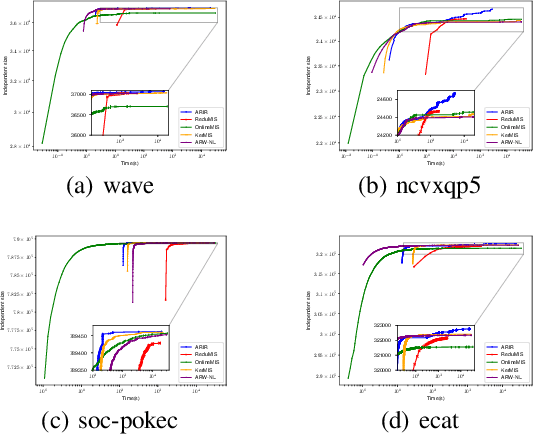
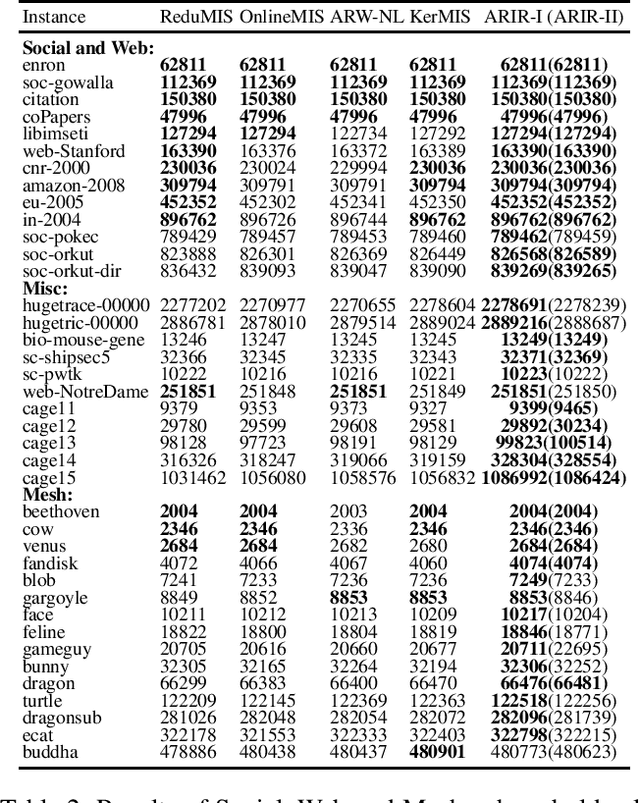
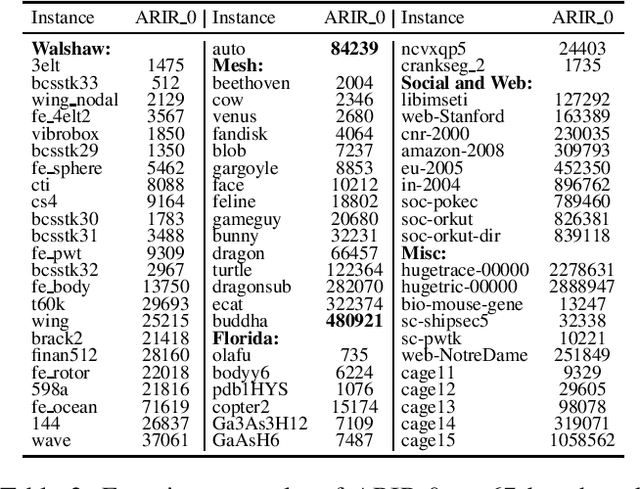
The maximum independent set (MIS) problem, a classical NP-hard problem with extensive applications in various areas, aims to find a largest set of vertices with no edge among them. Due to its computational intractability, it is difficult to solve the MIS problem effectively, especially on large graphs. Employing heuristic approaches to obtain a good solution within an acceptable amount of time has attracted much attention in literature. In this paper, we propose an efficient local search algorithm for MIS called ARIR, which consists of two main parts: an adaptive local search framework, and a novel inexact efficient reduction rule to simplify instances. We conduct experiments on five benchmarks, encompassing 92 instances. Compared with four state-of-the-art algorithms, ARIR offers the best accuracy on 89 instances and obtains competitive results on the three remaining instances.