Learning nonnegative matrix factorizations from compressed data

We propose a flexible and theoretically supported framework for scalable nonnegative matrix factorization. The goal is to find nonnegative low-rank components directly from compressed measurements, accessing the original data only once or twice. We consider compression through randomized sketching methods that can be adapted to the data, or can be oblivious. We formulate optimization problems that only depend on the compressed data, but which can recover a nonnegative factorization which closely approximates the original matrix. The defined problems can be approached with a variety of algorithms, and in particular, we discuss variations of the popular multiplicative updates method for these compressed problems. We demonstrate the success of our approaches empirically and validate their performance in real-world applications.

Higher-Order Newton Methods with Polynomial Work per Iteration

We present generalizations of Newton's method that incorporate derivatives of an arbitrary order $d$ but maintain a polynomial dependence on dimension in their cost per iteration. At each step, our $d^{\text{th}}$-order method uses semidefinite programming to construct and minimize a sum of squares-convex approximation to the $d^{\text{th}}$-order Taylor expansion of the function we wish to minimize. We prove that our $d^{\text{th}}$-order method has local convergence of order $d$. This results in lower oracle complexity compared to the classical Newton method. We show on numerical examples that basins of attraction around local minima can get larger as $d$ increases. Under additional assumptions, we present a modified algorithm, again with polynomial cost per iteration, which is globally convergent and has local convergence of order $d$.

Safely Learning Dynamical Systems

A fundamental challenge in learning an unknown dynamical system is to reduce model uncertainty by making measurements while maintaining safety. In this work, we formulate a mathematical definition of what it means to safely learn a dynamical system by sequentially deciding where to initialize the next trajectory. In our framework, the state of the system is required to stay within a safety region for a horizon of $T$ time steps under the action of all dynamical systems that (i) belong to a given initial uncertainty set, and (ii) are consistent with the information gathered so far. For our first set of results, we consider the setting of safely learning a linear dynamical system involving $n$ states. For the case $T=1$, we present a linear programming-based algorithm that either safely recovers the true dynamics from at most $n$ trajectories, or certifies that safe learning is impossible. For $T=2$, we give a semidefinite representation of the set of safe initial conditions and show that $\lceil n/2 \rceil$ trajectories generically suffice for safe learning. Finally, for $T = \infty$, we provide semidefinite representable inner approximations of the set of safe initial conditions and show that one trajectory generically suffices for safe learning. Our second set of results concerns the problem of safely learning a general class of nonlinear dynamical systems. For the case $T=1$, we give a second-order cone programming based representation of the set of safe initial conditions. For $T=\infty$, we provide semidefinite representable inner approximations to the set of safe initial conditions. We show how one can safely collect trajectories and fit a polynomial model of the nonlinear dynamics that is consistent with the initial uncertainty set and best agrees with the observations.

Safely Learning Dynamical Systems from Short Trajectories

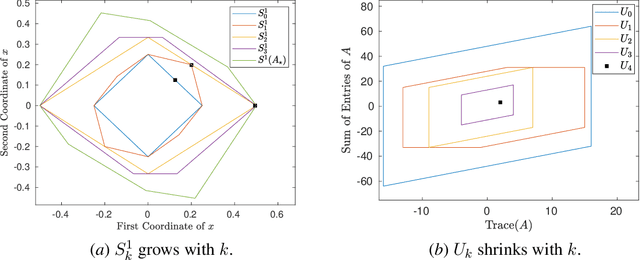
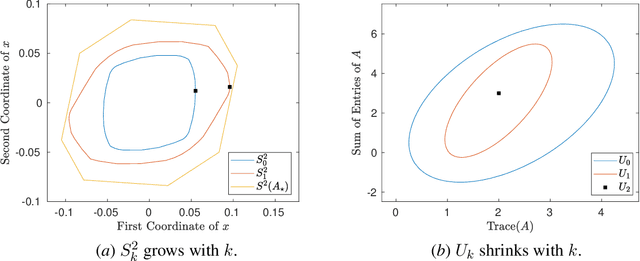
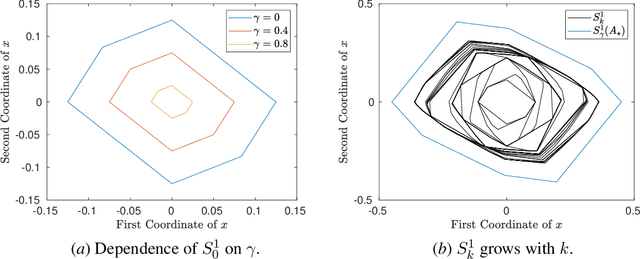
A fundamental challenge in learning to control an unknown dynamical system is to reduce model uncertainty by making measurements while maintaining safety. In this work, we formulate a mathematical definition of what it means to safely learn a dynamical system by sequentially deciding where to initialize the next trajectory. In our framework, the state of the system is required to stay within a given safety region under the (possibly repeated) action of all dynamical systems that are consistent with the information gathered so far. For our first two results, we consider the setting of safely learning linear dynamics. We present a linear programming-based algorithm that either safely recovers the true dynamics from trajectories of length one, or certifies that safe learning is impossible. We also give an efficient semidefinite representation of the set of initial conditions whose resulting trajectories of length two are guaranteed to stay in the safety region. For our final result, we study the problem of safely learning a nonlinear dynamical system. We give a second-order cone programming based representation of the set of initial conditions that are guaranteed to remain in the safety region after one application of the system dynamics.