SPAM: Stochastic Proximal Point Method with Momentum Variance Reduction for Non-convex Cross-Device Federated Learning

Cross-device training is a crucial subfield of federated learning, where the number of clients can reach into the billions. Standard approaches and local methods are prone to issues such as client drift and insensitivity to data similarities. We propose a novel algorithm (SPAM) for cross-device federated learning with non-convex losses, which solves both issues. We provide sharp analysis under second-order (Hessian) similarity, a condition satisfied by a variety of machine learning problems in practice. Additionally, we extend our results to the partial participation setting, where a cohort of selected clients communicate with the server at each communication round. Our method is the first in its kind, that does not require the smoothness of the objective and provably benefits from clients having similar data.

MAST: Model-Agnostic Sparsified Training

We introduce a novel optimization problem formulation that departs from the conventional way of minimizing machine learning model loss as a black-box function. Unlike traditional formulations, the proposed approach explicitly incorporates an initially pre-trained model and random sketch operators, allowing for sparsification of both the model and gradient during training. We establish insightful properties of the proposed objective function and highlight its connections to the standard formulation. Furthermore, we present several variants of the Stochastic Gradient Descent (SGD) method adapted to the new problem formulation, including SGD with general sampling, a distributed version, and SGD with variance reduction techniques. We achieve tighter convergence rates and relax assumptions, bridging the gap between theoretical principles and practical applications, covering several important techniques such as Dropout and Sparse training. This work presents promising opportunities to enhance the theoretical understanding of model training through a sparsification-aware optimization approach.

Towards a Better Theoretical Understanding of Independent Subnetwork Training

Modern advancements in large-scale machine learning would be impossible without the paradigm of data-parallel distributed computing. Since distributed computing with large-scale models imparts excessive pressure on communication channels, significant recent research has been directed toward co-designing communication compression strategies and training algorithms with the goal of reducing communication costs. While pure data parallelism allows better data scaling, it suffers from poor model scaling properties. Indeed, compute nodes are severely limited by memory constraints, preventing further increases in model size. For this reason, the latest achievements in training giant neural network models also rely on some form of model parallelism. In this work, we take a closer theoretical look at Independent Subnetwork Training (IST), which is a recently proposed and highly effective technique for solving the aforementioned problems. We identify fundamental differences between IST and alternative approaches, such as distributed methods with compressed communication, and provide a precise analysis of its optimization performance on a quadratic model.

Shifted Compression Framework: Generalizations and Improvements

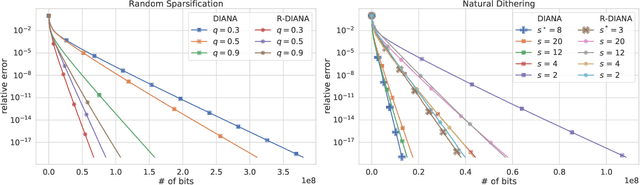
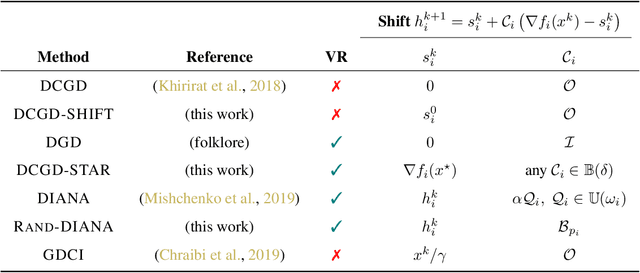
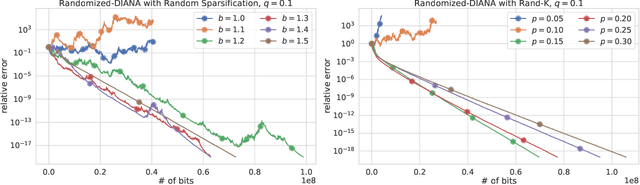
Communication is one of the key bottlenecks in the distributed training of large-scale machine learning models, and lossy compression of exchanged information, such as stochastic gradients or models, is one of the most effective instruments to alleviate this issue. Among the most studied compression techniques is the class of unbiased compression operators with variance bounded by a multiple of the square norm of the vector we wish to compress. By design, this variance may remain high, and only diminishes if the input vector approaches zero. However, unless the model being trained is overparameterized, there is no a-priori reason for the vectors we wish to compress to approach zero during the iterations of classical methods such as distributed compressed {\sf SGD}, which has adverse effects on the convergence speed. Due to this issue, several more elaborate and seemingly very different algorithms have been proposed recently, with the goal of circumventing this issue. These methods are based on the idea of compressing the {\em difference} between the vector we would normally wish to compress and some auxiliary vector which changes throughout the iterative process. In this work we take a step back, and develop a unified framework for studying such methods, conceptually, and theoretically. Our framework incorporates methods compressing both gradients and models, using unbiased and biased compressors, and sheds light on the construction of the auxiliary vectors. Furthermore, our general framework can lead to the improvement of several existing algorithms, and can produce new algorithms. Finally, we performed several numerical experiments which illustrate and support our theoretical findings.

Certified Robustness in Federated Learning

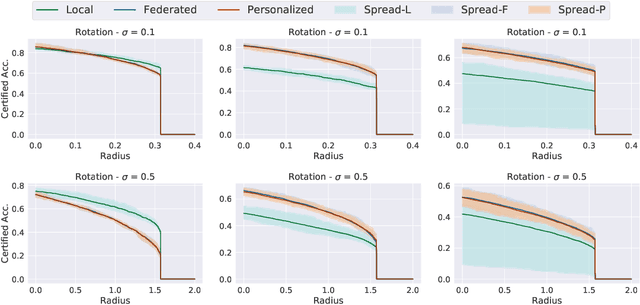
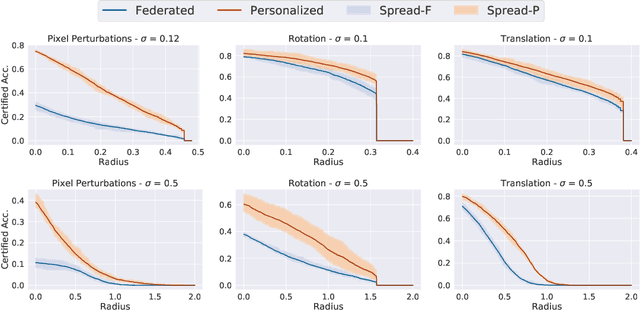
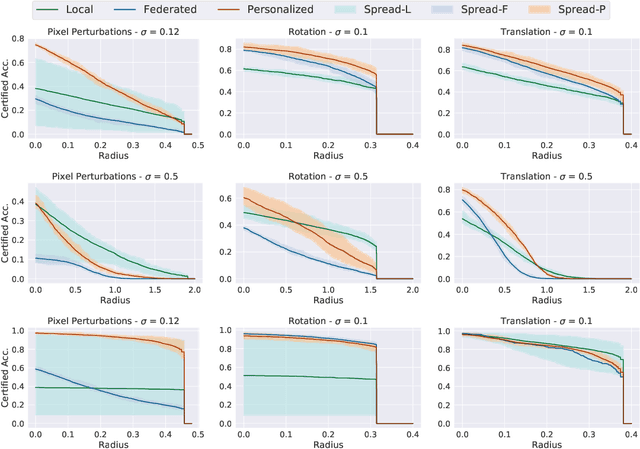
Federated learning has recently gained significant attention and popularity due to its effectiveness in training machine learning models on distributed data privately. However, as in the single-node supervised learning setup, models trained in federated learning suffer from vulnerability to imperceptible input transformations known as adversarial attacks, questioning their deployment in security-related applications. In this work, we study the interplay between federated training, personalization, and certified robustness. In particular, we deploy randomized smoothing, a widely-used and scalable certification method, to certify deep networks trained on a federated setup against input perturbations and transformations. We find that the simple federated averaging technique is effective in building not only more accurate, but also more certifiably-robust models, compared to training solely on local data. We further analyze personalization, a popular technique in federated training that increases the model's bias towards local data, on robustness. We show several advantages of personalization over both~(that is, only training on local data and federated training) in building more robust models with faster training. Finally, we explore the robustness of mixtures of global and local~(\ie personalized) models, and find that the robustness of local models degrades as they diverge from the global model

ADOM: Accelerated Decentralized Optimization Method for Time-Varying Networks

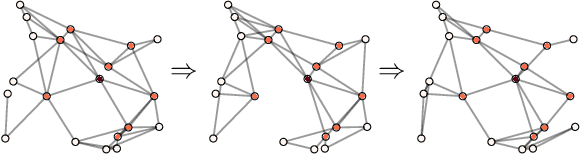
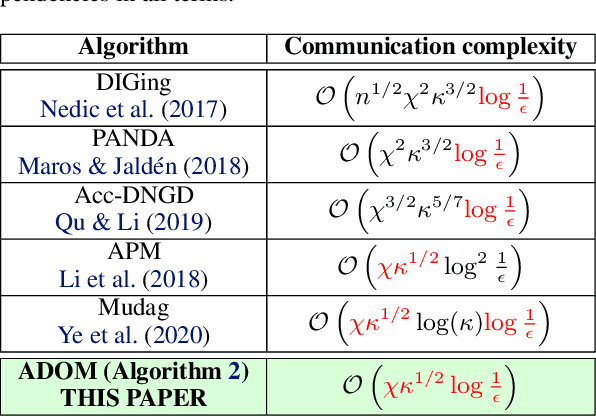
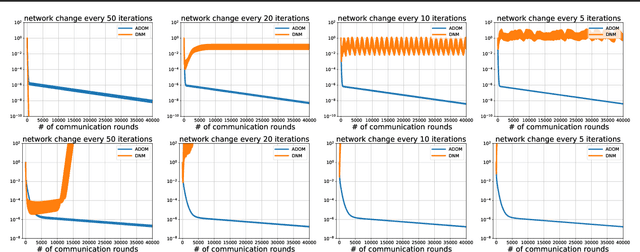
We propose ADOM - an accelerated method for smooth and strongly convex decentralized optimization over time-varying networks. ADOM uses a dual oracle, i.e., we assume access to the gradient of the Fenchel conjugate of the individual loss functions. Up to a constant factor, which depends on the network structure only, its communication complexity is the same as that of accelerated Nesterov gradient method (Nesterov, 2003). To the best of our knowledge, only the algorithm of Rogozin et al. (2019) has a convergence rate with similar properties. However, their algorithm converges under the very restrictive assumption that the number of network changes can not be greater than a tiny percentage of the number of iterations. This assumption is hard to satisfy in practice, as the network topology changes usually can not be controlled. In contrast, ADOM merely requires the network to stay connected throughout time.

Uncertainty Principle for Communication Compression in Distributed and Federated Learning and the Search for an Optimal Compressor

In order to mitigate the high communication cost in distributed and federated learning, various vector compression schemes, such as quantization, sparsification and dithering, have become very popular. In designing a compression method, one aims to communicate as few bits as possible, which minimizes the cost per communication round, while at the same time attempting to impart as little distortion (variance) to the communicated messages as possible, which minimizes the adverse effect of the compression on the overall number of communication rounds. However, intuitively, these two goals are fundamentally in conflict: the more compression we allow, the more distorted the messages become. We formalize this intuition and prove an {\em uncertainty principle} for randomized compression operators, thus quantifying this limitation mathematically, and {\em effectively providing lower bounds on what might be achievable with communication compression}. Motivated by these developments, we call for the search for the optimal compression operator. In an attempt to take a first step in this direction, we construct a new unbiased compression method inspired by the Kashin representation of vectors, which we call {\em Kashin compression (KC)}. In contrast to all previously proposed compression mechanisms, we prove that KC enjoys a {\em dimension independent} variance bound with an explicit formula even in the regime when only a few bits need to be communicate per each vector entry. We show how KC can be provably and efficiently combined with several existing optimization algorithms, in all cases leading to communication complexity improvements on previous state of the art.

Revisiting Stochastic Extragradient

We consider a new extension of the extragradient method that is motivated by approximating implicit updates. Since in a recent work~\cite{chavdarova2019reducing} it was shown that the existing stochastic extragradient algorithm (called mirror-prox) of~\cite{juditsky2011solving} diverges on a simple bilinear problem, we prove guarantees for solving variational inequality that are more general than in~\cite{juditsky2011solving}. Furthermore, we illustrate numerically that the proposed variant converges faster than many other methods on the example of~\cite{chavdarova2019reducing}. We also discuss how extragradient can be applied to training Generative Adversarial Networks (GANs). Our experiments on GANs demonstrate that the introduced approach may make the training faster in terms of data passes, while its higher iteration complexity makes the advantage smaller. To further accelerate method's convergence on problems such as bilinear minimax, we combine the extragradient step with negative momentum~\cite{gidel2018negative} and discuss the optimal momentum value.

SGD: General Analysis and Improved Rates

We propose a general yet simple theorem describing the convergence of SGD under the arbitrary sampling paradigm. Our theorem describes the convergence of an infinite array of variants of SGD, each of which is associated with a specific probability law governing the data selection rule used to form mini-batches. This is the first time such an analysis is performed, and most of our variants of SGD were never explicitly considered in the literature before. Our analysis relies on the recently introduced notion of expected smoothness and does not rely on a uniform bound on the variance of the stochastic gradients. By specializing our theorem to different mini-batching strategies, such as sampling with replacement and independent sampling, we derive exact expressions for the stepsize as a function of the mini-batch size. With this we can also determine the mini-batch size that optimizes the total complexity, and show explicitly that as the variance of the stochastic gradient evaluated at the minimum grows, so does the optimal mini-batch size. For zero variance, the optimal mini-batch size is one. Moreover, we prove insightful stepsize-switching rules which describe when one should switch from a constant to a decreasing stepsize regime.