Optimal Probing with Statistical Guarantees for Network Monitoring at Scale

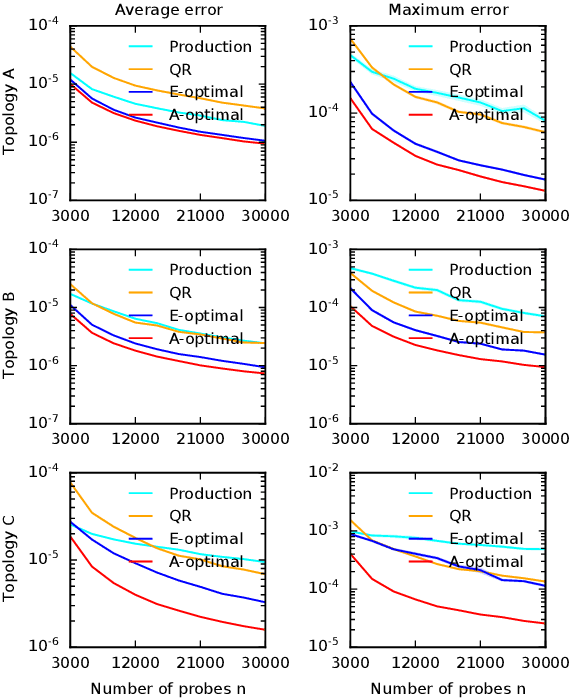
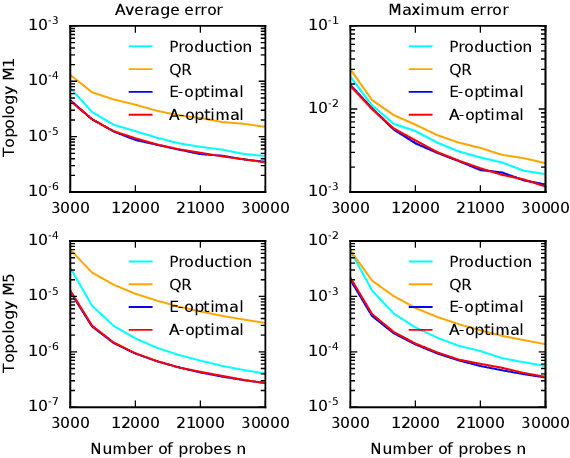
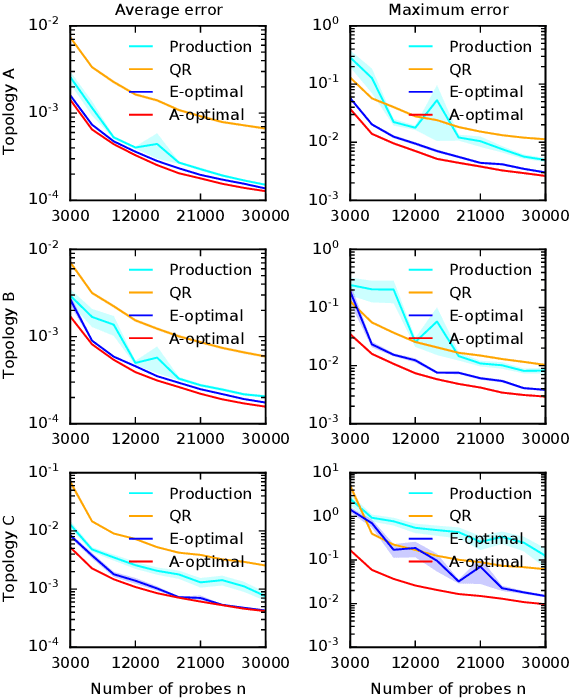
Cloud networks are difficult to monitor because they grow rapidly and the budgets for monitoring them are limited. We propose a framework for estimating network metrics, such as latency and packet loss, with guarantees on estimation errors for a fixed monitoring budget. Our proposed algorithms produce a distribution of probes across network paths, which we then monitor; and are based on A- and E-optimal experimental designs in statistics. Unfortunately, these designs are too computationally costly to use at production scale. We propose their scalable and near-optimal approximations based on the Frank-Wolfe algorithm. We validate our approaches in simulation on real network topologies, and also using a production probing system in a real cloud network. We show major gains in reducing the probing budget compared to both production and academic baselines, while maintaining low estimation errors, even with very low probing budgets.

Time Series Analysis via Matrix Estimation

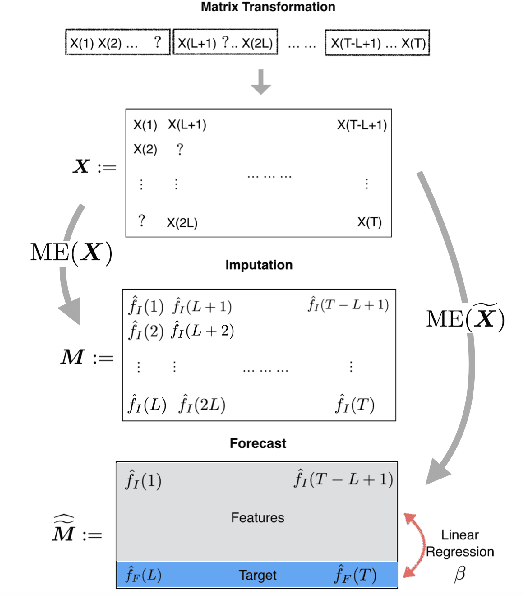
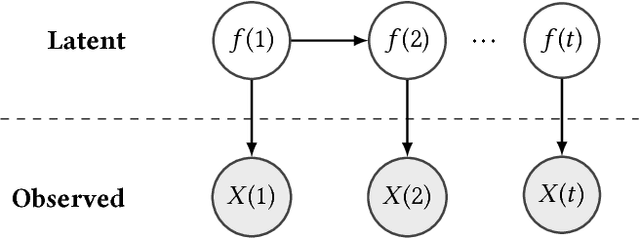
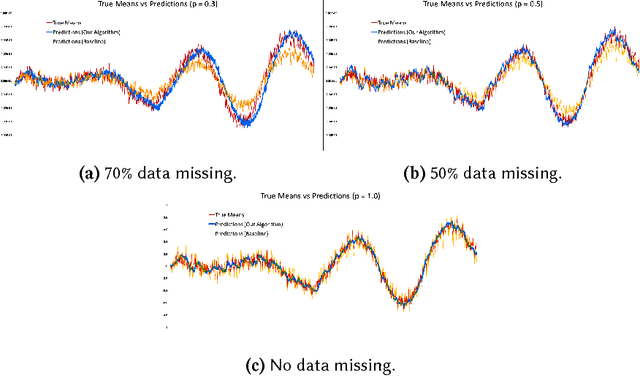
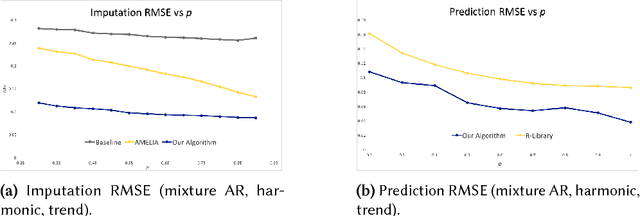
We propose an algorithm to impute and forecast a time series by transforming the observed time series into a matrix, utilizing matrix estimation to recover missing values and de-noise observed entries, and performing linear regression to make predictions. At the core of our analysis is a representation result, which states that for a large model class, the transformed matrix obtained from the time series via our algorithm is (approximately) low-rank. This, in effect, generalizes the widely used Singular Spectrum Analysis (SSA) in literature, and allows us to establish a rigorous link between time series analysis and matrix estimation. The key is to construct a matrix with non-overlapping entries rather than with the Hankel matrix as done in the literature, including in SSA. We provide finite sample analysis for imputation and prediction leading to the asymptotic consistency of our method. A salient feature of our algorithm is that it is model agnostic both with respect to the underlying time dynamics as well as the noise model in the observations. Being noise agnostic makes our algorithm applicable to the setting where the state is hidden and we only have access to its noisy observations a la a Hidden Markov Model, e.g., observing a Poisson process with a time-varying parameter without knowing that the process is Poisson, but still recovering the time-varying parameter accurately. As part of the forecasting algorithm, an important task is to perform regression with noisy observations of the features a la an error- in-variable regression. In essence, our approach suggests a matrix estimation based method for such a setting, which could be of interest in its own right. Through synthetic and real-world datasets, we demonstrate that our algorithm outperforms standard software packages (including R libraries) in the presence of missing data as well as high levels of noise.

Robust Synthetic Control

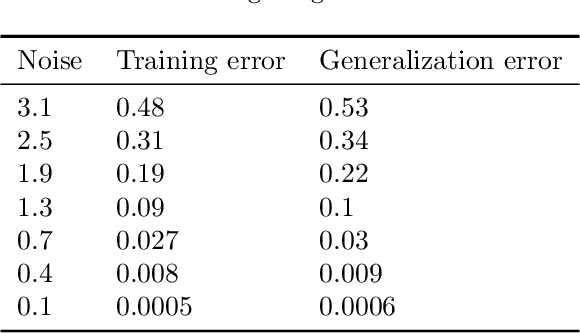
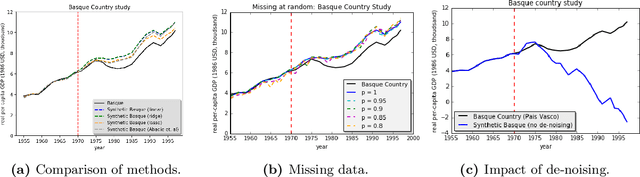
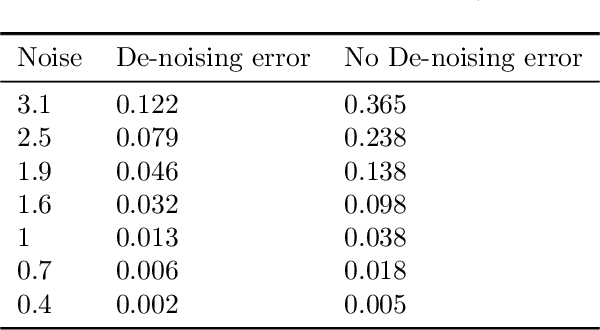
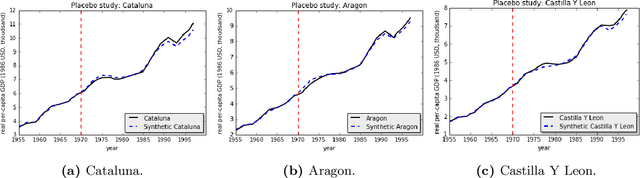
We present a robust generalization of the synthetic control method for comparative case studies. Like the classical method, we present an algorithm to estimate the unobservable counterfactual of a treatment unit. A distinguishing feature of our algorithm is that of de-noising the data matrix via singular value thresholding, which renders our approach robust in multiple facets: it automatically identifies a good subset of donors, overcomes the challenges of missing data, and continues to work well in settings where covariate information may not be provided. To begin, we establish the condition under which the fundamental assumption in synthetic control-like approaches holds, i.e. when the linear relationship between the treatment unit and the donor pool prevails in both the pre- and post-intervention periods. We provide the first finite sample analysis for a broader class of models, the Latent Variable Model, in contrast to Factor Models previously considered in the literature. Further, we show that our de-noising procedure accurately imputes missing entries, producing a consistent estimator of the underlying signal matrix provided $p = \Omega( T^{-1 + \zeta})$ for some $\zeta > 0$; here, $p$ is the fraction of observed data and $T$ is the time interval of interest. Under the same setting, we prove that the mean-squared-error (MSE) in our prediction estimation scales as $O(\sigma^2/p + 1/\sqrt{T})$, where $\sigma^2$ is the noise variance. Using a data aggregation method, we show that the MSE can be made as small as $O(T^{-1/2+\gamma})$ for any $\gamma \in (0, 1/2)$, leading to a consistent estimator. We also introduce a Bayesian framework to quantify the model uncertainty through posterior probabilities. Our experiments, using both real-world and synthetic datasets, demonstrate that our robust generalization yields an improvement over the classical synthetic control method.