Multivector Neurons: Better and Faster O(n)-Equivariant Clifford Graph Neural Networks

Most current deep learning models equivariant to $O(n)$ or $SO(n)$ either consider mostly scalar information such as distances and angles or have a very high computational complexity. In this work, we test a few novel message passing graph neural networks (GNNs) based on Clifford multivectors, structured similarly to other prevalent equivariant models in geometric deep learning. Our approach leverages efficient invariant scalar features while simultaneously performing expressive learning on multivector representations, particularly through the use of the equivariant geometric product operator. By integrating these elements, our methods outperform established efficient baseline models on an N-Body simulation task and protein denoising task while maintaining a high efficiency. In particular, we push the state-of-the-art error on the N-body dataset to 0.0035 (averaged over 3 runs); an 8% improvement over recent methods. Our implementation is available on Github.

Clifford-Steerable Convolutional Neural Networks

We present Clifford-Steerable Convolutional Neural Networks (CS-CNNs), a novel class of $\mathrm{E}(p, q)$-equivariant CNNs. CS-CNNs process multivector fields on pseudo-Euclidean spaces $\mathbb{R}^{p,q}$. They cover, for instance, $\mathrm{E}(3)$-equivariance on $\mathbb{R}^3$ and Poincar\'e-equivariance on Minkowski spacetime $\mathbb{R}^{1,3}$. Our approach is based on an implicit parametrization of $\mathrm{O}(p,q)$-steerable kernels via Clifford group equivariant neural networks. We significantly and consistently outperform baseline methods on fluid dynamics as well as relativistic electrodynamics forecasting tasks.

Clifford Group Equivariant Simplicial Message Passing Networks

We introduce Clifford Group Equivariant Simplicial Message Passing Networks, a method for steerable E(n)-equivariant message passing on simplicial complexes. Our method integrates the expressivity of Clifford group-equivariant layers with simplicial message passing, which is topologically more intricate than regular graph message passing. Clifford algebras include higher-order objects such as bivectors and trivectors, which express geometric features (e.g., areas, volumes) derived from vectors. Using this knowledge, we represent simplex features through geometric products of their vertices. To achieve efficient simplicial message passing, we share the parameters of the message network across different dimensions. Additionally, we restrict the final message to an aggregation of the incoming messages from different dimensions, leading to what we term shared simplicial message passing. Experimental results show that our method is able to outperform both equivariant and simplicial graph neural networks on a variety of geometric tasks.

Rolling Diffusion Models

Diffusion models have recently been increasingly applied to temporal data such as video, fluid mechanics simulations, or climate data. These methods generally treat subsequent frames equally regarding the amount of noise in the diffusion process. This paper explores Rolling Diffusion: a new approach that uses a sliding window denoising process. It ensures that the diffusion process progressively corrupts through time by assigning more noise to frames that appear later in a sequence, reflecting greater uncertainty about the future as the generation process unfolds. Empirically, we show that when the temporal dynamics are complex, Rolling Diffusion is superior to standard diffusion. In particular, this result is demonstrated in a video prediction task using the Kinetics-600 video dataset and in a chaotic fluid dynamics forecasting experiment.

On the Effectiveness of Hybrid Mutual Information Estimation

Estimating the mutual information from samples from a joint distribution is a challenging problem in both science and engineering. In this work, we realize a variational bound that generalizes both discriminative and generative approaches. Using this bound, we propose a hybrid method to mitigate their respective shortcomings. Further, we propose Predictive Quantization (PQ): a simple generative method that can be easily combined with discriminative estimators for minimal computational overhead. Our propositions yield a tighter bound on the information thanks to the reduced variance of the estimator. We test our methods on a challenging task of correlated high-dimensional Gaussian distributions and a stochastic process involving a system of free particles subjected to a fixed energy landscape. Empirical results show that hybrid methods consistently improved mutual information estimates when compared to the corresponding discriminative counterpart.

Clifford Group Equivariant Neural Networks

We introduce Clifford Group Equivariant Neural Networks: a novel approach for constructing $\mathrm{E}(n)$-equivariant networks. We identify and study the $\textit{Clifford group}$, a subgroup inside the Clifford algebra, whose definition we slightly adjust to achieve several favorable properties. Primarily, the group's action forms an orthogonal automorphism that extends beyond the typical vector space to the entire Clifford algebra while respecting the multivector grading. This leads to several non-equivalent subrepresentations corresponding to the multivector decomposition. Furthermore, we prove that the action respects not just the vector space structure of the Clifford algebra but also its multiplicative structure, i.e., the geometric product. These findings imply that every polynomial in multivectors, including their grade projections, constitutes an equivariant map with respect to the Clifford group, allowing us to parameterize equivariant neural network layers. Notable advantages are that these layers operate directly on a vector basis and elegantly generalize to any dimension. We demonstrate, notably from a single core implementation, state-of-the-art performance on several distinct tasks, including a three-dimensional $n$-body experiment, a four-dimensional Lorentz-equivariant high-energy physics experiment, and a five-dimensional convex hull experiment.

Geometric Clifford Algebra Networks

We propose Geometric Clifford Algebra Networks (GCANs) that are based on symmetry group transformations using geometric (Clifford) algebras. GCANs are particularly well-suited for representing and manipulating geometric transformations, often found in dynamical systems. We first review the quintessence of modern (plane-based) geometric algebra, which builds on isometries encoded as elements of the $\mathrm{Pin}(p,q,r)$ group. We then propose the concept of group action layers, which linearly combine object transformations using pre-specified group actions. Together with a new activation and normalization scheme, these layers serve as adjustable geometric templates that can be refined via gradient descent. Theoretical advantages are strongly reflected in the modeling of three-dimensional rigid body transformations as well as large-scale fluid dynamics simulations, showing significantly improved performance over traditional methods.

Normalizing Flows for Hierarchical Bayesian Analysis: A Gravitational Wave Population Study

We propose parameterizing the population distribution of the gravitational wave population modeling framework (Hierarchical Bayesian Analysis) with a normalizing flow. We first demonstrate the merit of this method on illustrative experiments and then analyze four parameters of the latest LIGO data release: primary mass, secondary mass, redshift, and effective spin. Our results show that despite the small and notoriously noisy dataset, the posterior predictive distributions (assuming a prior over the parameters of the flow) of the observed gravitational wave population recover structure that agrees with robust previous phenomenological modeling results while being less susceptible to biases introduced by less-flexible distribution models. Therefore, the method forms a promising flexible, reliable replacement for population inference distributions, even when data is highly noisy.

Self-Supervised Hybrid Inference in State-Space Models

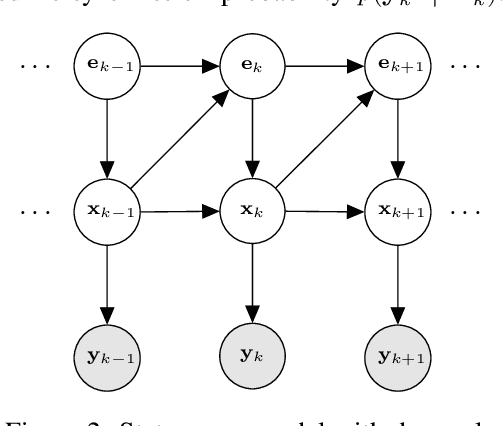
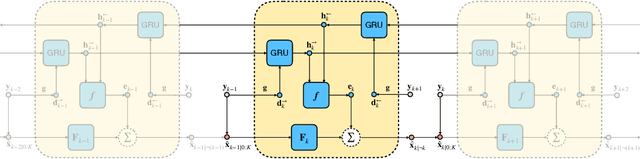
We perform approximate inference in state-space models that allow for nonlinear higher-order Markov chains in latent space. The conditional independencies of the generative model enable us to parameterize only an inference model, which learns to estimate clean states in a self-supervised manner using maximum likelihood. First, we propose a recurrent method that is trained directly on noisy observations. Afterward, we cast the model such that the optimization problem leads to an update scheme that backpropagates through a recursion similar to the classical Kalman filter and smoother. In scientific applications, domain knowledge can give a linear approximation of the latent transition maps. We can easily incorporate this knowledge into our model, leading to a hybrid inference approach. In contrast to other methods, experiments show that the hybrid method makes the inferred latent states physically more interpretable and accurate, especially in low-data regimes. Furthermore, we do not rely on an additional parameterization of the generative model or supervision via uncorrupted observations or ground truth latent states. Despite our model's simplicity, we obtain competitive results on the chaotic Lorenz system compared to a fully supervised approach and outperform a method based on variational inference.

Bayesian Modelling in Practice: Using Uncertainty to Improve Trustworthiness in Medical Applications

The Intensive Care Unit (ICU) is a hospital department where machine learning has the potential to provide valuable assistance in clinical decision making. Classical machine learning models usually only provide point-estimates and no uncertainty of predictions. In practice, uncertain predictions should be presented to doctors with extra care in order to prevent potentially catastrophic treatment decisions. In this work we show how Bayesian modelling and the predictive uncertainty that it provides can be used to mitigate risk of misguided prediction and to detect out-of-domain examples in a medical setting. We derive analytically a bound on the prediction loss with respect to predictive uncertainty. The bound shows that uncertainty can mitigate loss. Furthermore, we apply a Bayesian Neural Network to the MIMIC-III dataset, predicting risk of mortality of ICU patients. Our empirical results show that uncertainty can indeed prevent potential errors and reliably identifies out-of-domain patients. These results suggest that Bayesian predictive uncertainty can greatly improve trustworthiness of machine learning models in high-risk settings such as the ICU.