Electrostatics from Laplacian Eigenbasis for Neural Network Interatomic Potentials

Recent advances in neural network interatomic potentials have emerged as a promising research direction. However, popular deep learning models often lack auxiliary constraints grounded in physical laws, which could accelerate training and improve fidelity through physics-based regularization. In this work, we introduce $\Phi$-Module, a universal plugin module that enforces Poisson's equation within the message-passing framework to learn electrostatic interactions in a self-supervised manner. Specifically, each atom-wise representation is encouraged to satisfy a discretized Poisson's equation, making it possible to acquire a potential $\boldsymbol{\phi}$ and a corresponding charge density $\boldsymbol{\rho}$ linked to the learnable Laplacian eigenbasis coefficients of a given molecular graph. We then derive an electrostatic energy term, crucial for improved total energy predictions. This approach integrates seamlessly into any existing neural potential with insignificant computational overhead. Experiments on the OE62 and MD22 benchmarks confirm that models combined with $\Phi$-Module achieve robust improvements over baseline counterparts. For OE62 error reduction ranges from 4.5\% to 17.8\%, and for MD22, baseline equipped with $\Phi$-Module achieves best results on 5 out of 14 cases. Our results underscore how embedding a first-principles constraint in neural interatomic potentials can significantly improve performance while remaining hyperparameter-friendly, memory-efficient and lightweight in training. Code will be available at \href{https://github.com/dunnolab/phi-module}{dunnolab/phi-module}.

AdS-GNN -- a Conformally Equivariant Graph Neural Network

Conformal symmetries, i.e.\ coordinate transformations that preserve angles, play a key role in many fields, including physics, mathematics, computer vision and (geometric) machine learning. Here we build a neural network that is equivariant under general conformal transformations. To achieve this, we lift data from flat Euclidean space to Anti de Sitter (AdS) space. This allows us to exploit a known correspondence between conformal transformations of flat space and isometric transformations on the AdS space. We then build upon the fact that such isometric transformations have been extensively studied on general geometries in the geometric deep learning literature. We employ message-passing layers conditioned on the proper distance, yielding a computationally efficient framework. We validate our model on tasks from computer vision and statistical physics, demonstrating strong performance, improved generalization capacities, and the ability to extract conformal data such as scaling dimensions from the trained network.

Erwin: A Tree-based Hierarchical Transformer for Large-scale Physical Systems

Large-scale physical systems defined on irregular grids pose significant scalability challenges for deep learning methods, especially in the presence of long-range interactions and multi-scale coupling. Traditional approaches that compute all pairwise interactions, such as attention, become computationally prohibitive as they scale quadratically with the number of nodes. We present Erwin, a hierarchical transformer inspired by methods from computational many-body physics, which combines the efficiency of tree-based algorithms with the expressivity of attention mechanisms. Erwin employs ball tree partitioning to organize computation, which enables linear-time attention by processing nodes in parallel within local neighborhoods of fixed size. Through progressive coarsening and refinement of the ball tree structure, complemented by a novel cross-ball interaction mechanism, it captures both fine-grained local details and global features. We demonstrate Erwin's effectiveness across multiple domains, including cosmology, molecular dynamics, and particle fluid dynamics, where it consistently outperforms baseline methods both in accuracy and computational efficiency.

Clifford-Steerable Convolutional Neural Networks

We present Clifford-Steerable Convolutional Neural Networks (CS-CNNs), a novel class of $\mathrm{E}(p, q)$-equivariant CNNs. CS-CNNs process multivector fields on pseudo-Euclidean spaces $\mathbb{R}^{p,q}$. They cover, for instance, $\mathrm{E}(3)$-equivariance on $\mathbb{R}^3$ and Poincar\'e-equivariance on Minkowski spacetime $\mathbb{R}^{1,3}$. Our approach is based on an implicit parametrization of $\mathrm{O}(p,q)$-steerable kernels via Clifford group equivariant neural networks. We significantly and consistently outperform baseline methods on fluid dynamics as well as relativistic electrodynamics forecasting tasks.

Unveiling Empirical Pathologies of Laplace Approximation for Uncertainty Estimation

In this paper, we critically evaluate Bayesian methods for uncertainty estimation in deep learning, focusing on the widely applied Laplace approximation and its variants. Our findings reveal that the conventional method of fitting the Hessian matrix negatively impacts out-of-distribution (OOD) detection efficiency. We propose a different point of view, asserting that focusing solely on optimizing prior precision can yield more accurate uncertainty estimates in OOD detection while preserving adequate calibration metrics. Moreover, we demonstrate that this property is not connected to the training stage of a model but rather to its intrinsic properties. Through extensive experimental evaluation, we establish the superiority of our simplified approach over traditional methods in the out-of-distribution domain.

Catching Image Retrieval Generalization

The concepts of overfitting and generalization are vital for evaluating machine learning models. In this work, we show that the popular Recall@K metric depends on the number of classes in the dataset, which limits its ability to estimate generalization. To fix this issue, we propose a new metric, which measures retrieval performance, and, unlike Recall@K, estimates generalization. We apply the proposed metric to popular image retrieval methods and provide new insights about deep metric learning generalization.

Implicit Neural Convolutional Kernels for Steerable CNNs

Steerable convolutional neural networks (CNNs) provide a general framework for building neural networks equivariant to translations and other transformations belonging to an origin-preserving group $G$, such as reflections and rotations. They rely on standard convolutions with $G$-steerable kernels obtained by analytically solving the group-specific equivariance constraint imposed onto the kernel space. As the solution is tailored to a particular group $G$, the implementation of a kernel basis does not generalize to other symmetry transformations, which complicates the development of group equivariant models. We propose using implicit neural representation via multi-layer perceptrons (MLPs) to parameterize $G$-steerable kernels. The resulting framework offers a simple and flexible way to implement Steerable CNNs and generalizes to any group $G$ for which a $G$-equivariant MLP can be built. We apply our method to point cloud (ModelNet-40) and molecular data (QM9) and demonstrate a significant improvement in performance compared to standard Steerable CNNs.

Amortized Bayesian Inference of GISAXS Data with Normalizing Flows

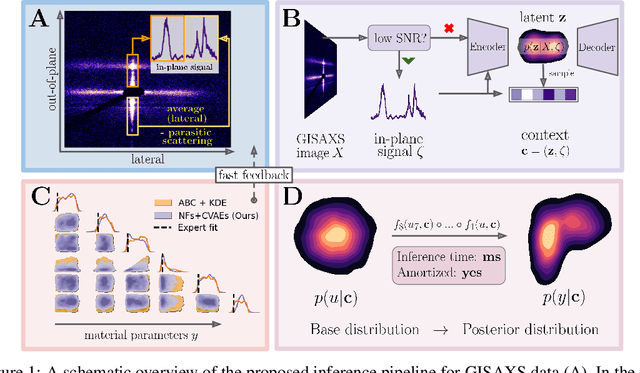
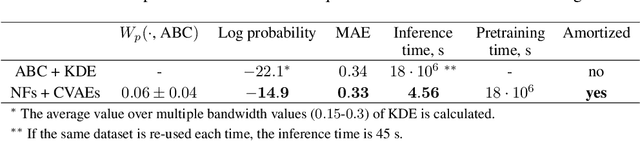
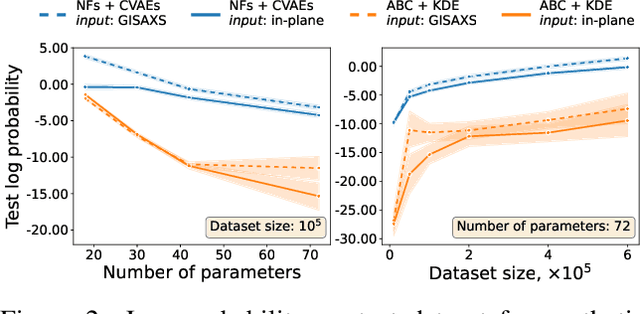
Grazing-Incidence Small-Angle X-ray Scattering (GISAXS) is a modern imaging technique used in material research to study nanoscale materials. Reconstruction of the parameters of an imaged object imposes an ill-posed inverse problem that is further complicated when only an in-plane GISAXS signal is available. Traditionally used inference algorithms such as Approximate Bayesian Computation (ABC) rely on computationally expensive scattering simulation software, rendering analysis highly time-consuming. We propose a simulation-based framework that combines variational auto-encoders and normalizing flows to estimate the posterior distribution of object parameters given its GISAXS data. We apply the inference pipeline to experimental data and demonstrate that our method reduces the inference cost by orders of magnitude while producing consistent results with ABC.

Learning Generative Factors of Neuroimaging Data with Variational auto-encoders

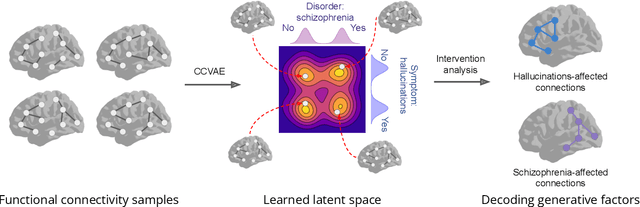
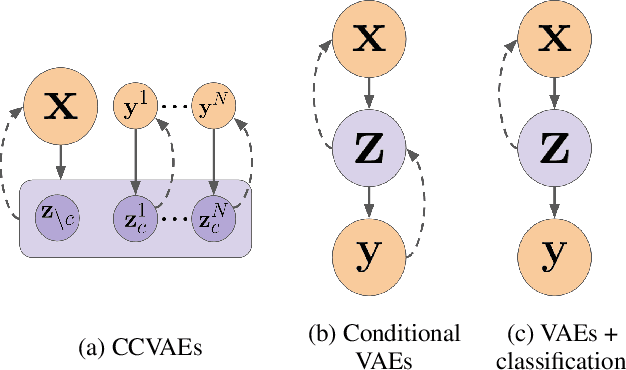
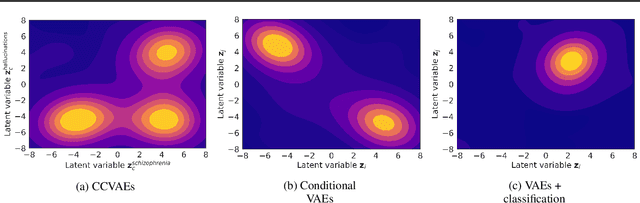
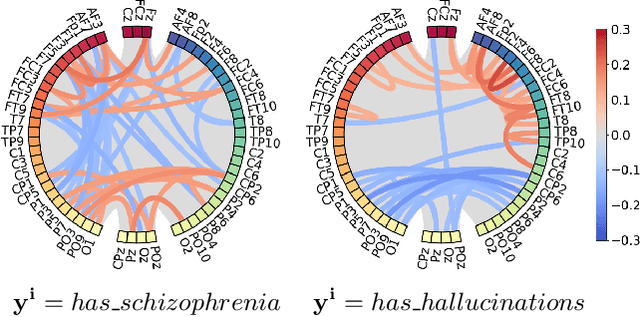
Neuroimaging techniques produce high-dimensional, stochastic data from which it might be challenging to extract high-level knowledge about the phenomena of interest. We address this challenge by applying the framework of generative modelling to 1) classify multiple pathologies, 2) recover neurological mechanisms of those pathologies in a data-driven manner and 3) learn robust representations of neuroimaging data. We illustrate the applicability of the proposed approach to identifying schizophrenia, either followed or not by auditory verbal hallucinations. We further demonstrate the ability of the framework to learn disease-related mechanisms that are consistent with current domain knowledge. We also compare the proposed framework with several benchmark approaches and indicate its advantages.

Investigating Brain Connectivity with Graph Neural Networks and GNNExplainer

Functional connectivity plays an essential role in modern neuroscience. The modality sheds light on the brain's functional and structural aspects, including mechanisms behind multiple pathologies. One such pathology is schizophrenia which is often followed by auditory verbal hallucinations. The latter is commonly studied by observing functional connectivity during speech processing. In this work, we have made a step toward an in-depth examination of functional connectivity during a dichotic listening task via deep learning for three groups of people: schizophrenia patients with and without auditory verbal hallucinations and healthy controls. We propose a graph neural network-based framework within which we represent EEG data as signals in the graph domain. The framework allows one to 1) predict a brain mental disorder based on EEG recording, 2) differentiate the listening state from the resting state for each group and 3) recognize characteristic task-depending connectivity. Experimental results show that the proposed model can differentiate between the above groups with state-of-the-art performance. Besides, it provides a researcher with meaningful information regarding each group's functional connectivity, which we validated on the current domain knowledge.