Grappa: Gradient-Only Communication for Scalable Graph Neural Network Training

Cross-partition edges dominate the cost of distributed GNN training: fetching remote features and activations per iteration overwhelms the network as graphs deepen and partition counts grow. Grappa is a distributed GNN training framework that enforces gradient-only communication: during each iteration, partitions train in isolation and exchange only gradients for the global update. To recover accuracy lost to isolation, Grappa (i) periodically repartitions to expose new neighborhoods and (ii) applies a lightweight coverage-corrected gradient aggregation inspired by importance sampling. We prove the corrected estimator is asymptotically unbiased under standard support and boundedness assumptions, and we derive a batch-level variant for compatibility with common deep-learning packages that minimizes mean-squared deviation from the ideal node-level correction. We also introduce a shrinkage version that improves stability in practice. Empirical results on real and synthetic graphs show that Grappa trains GNNs 4 times faster on average (up to 13 times) than state-of-the-art systems, achieves better accuracy especially for deeper models, and sustains training at the trillion-edge scale on commodity hardware. Grappa is model-agnostic, supports full-graph and mini-batch training, and does not rely on high-bandwidth interconnects or caching.

Networked Restless Multi-Armed Bandits for Mobile Interventions

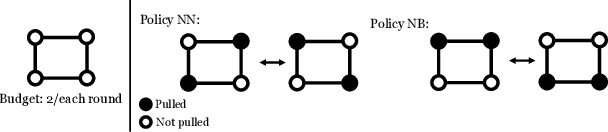
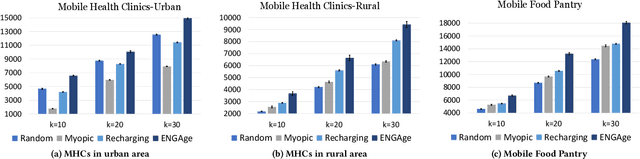
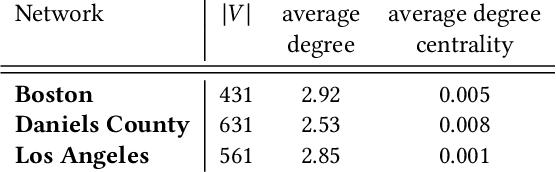
Motivated by a broad class of mobile intervention problems, we propose and study restless multi-armed bandits (RMABs) with network effects. In our model, arms are partially recharging and connected through a graph, so that pulling one arm also improves the state of neighboring arms, significantly extending the previously studied setting of fully recharging bandits with no network effects. In mobile interventions, network effects may arise due to regular population movements (such as commuting between home and work). We show that network effects in RMABs induce strong reward coupling that is not accounted for by existing solution methods. We propose a new solution approach for networked RMABs, exploiting concavity properties which arise under natural assumptions on the structure of intervention effects. We provide sufficient conditions for optimality of our approach in idealized settings and demonstrate that it empirically outperforms state-of-the art baselines in three mobile intervention domains using real-world graphs.

Efficient Algorithms for Finite Horizon and Streaming Restless Multi-Armed Bandit Problems

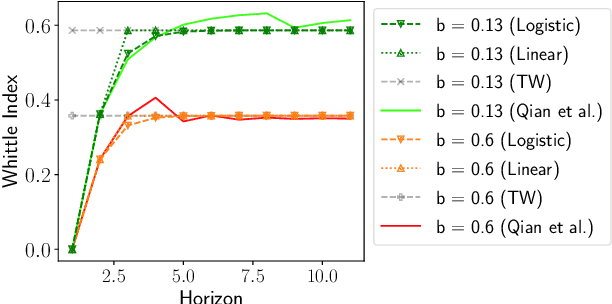
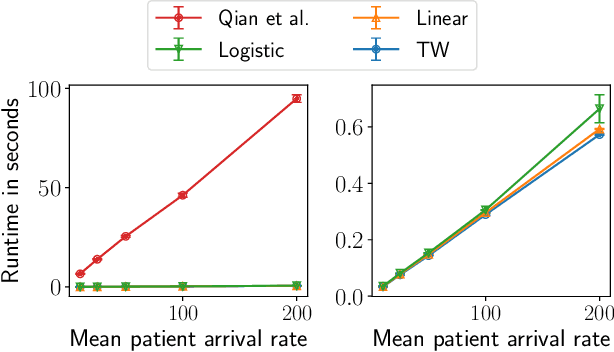
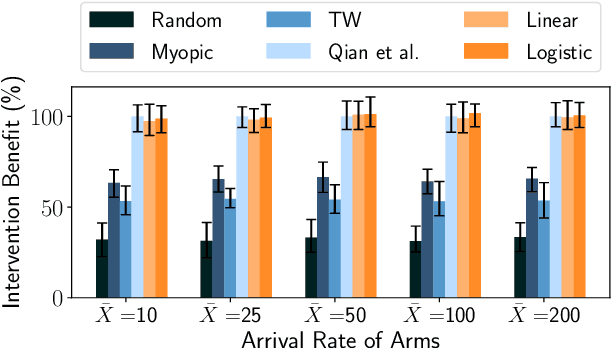
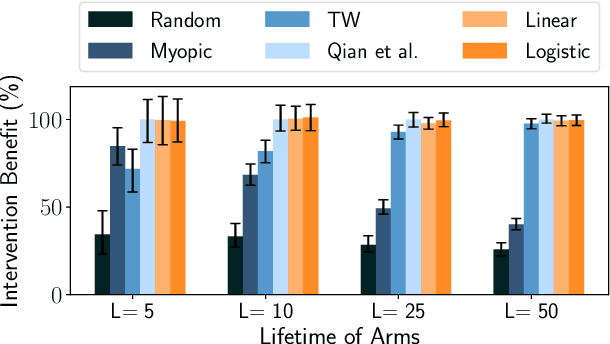
Restless Multi-Armed Bandits (RMABs) have been popularly used to model limited resource allocation problems. Recently, these have been employed for health monitoring and intervention planning problems. However, the existing approaches fail to account for the arrival of new patients and the departure of enrolled patients from a treatment program. To address this challenge, we formulate a streaming bandit (S-RMAB) framework, a generalization of RMABs where heterogeneous arms arrive and leave under possibly random streams. We propose a new and scalable approach to computing index-based solutions. We start by proving that index values decrease for short residual lifetimes, a phenomenon that we call index decay. We then provide algorithms designed to capture index decay without having to solve the costly finite horizon problem, thereby lowering the computational complexity compared to existing methods.We evaluate our approach via simulations run on real-world data obtained from a tuberculosis intervention planning task as well as multiple other synthetic domains. Our algorithms achieve an over 150x speed-up over existing methods in these tasks without loss in performance. These findings are robust across multiple domains.