MOT20: A benchmark for multi object tracking in crowded scenes

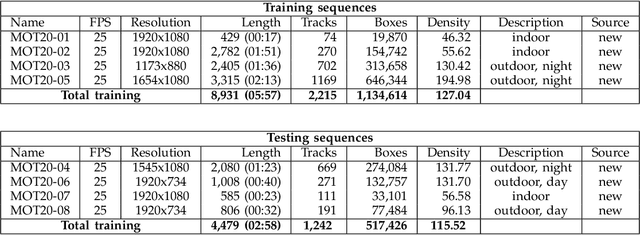
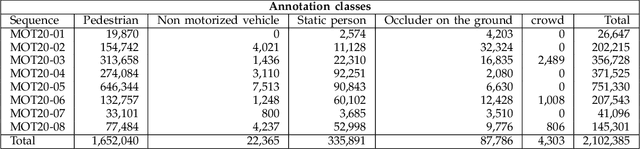
Standardized benchmarks are crucial for the majority of computer vision applications. Although leaderboards and ranking tables should not be over-claimed, benchmarks often provide the most objective measure of performance and are therefore important guides for research. The benchmark for Multiple Object Tracking, MOTChallenge, was launched with the goal to establish a standardized evaluation of multiple object tracking methods. The challenge focuses on multiple people tracking, since pedestrians are well studied in the tracking community, and precise tracking and detection has high practical relevance. Since the first release, MOT15, MOT16, and MOT17 have tremendously contributed to the community by introducing a clean dataset and precise framework to benchmark multi-object trackers. In this paper, we present our MOT20benchmark, consisting of 8 new sequences depicting very crowded challenging scenes. The benchmark was presented first at the 4thBMTT MOT Challenge Workshop at the Computer Vision and Pattern Recognition Conference (CVPR) 2019, and gives to chance to evaluate state-of-the-art methods for multiple object tracking when handling extremely crowded scenarios.

Optimization of Graph Total Variation via Active-Set-based Combinatorial Reconditioning

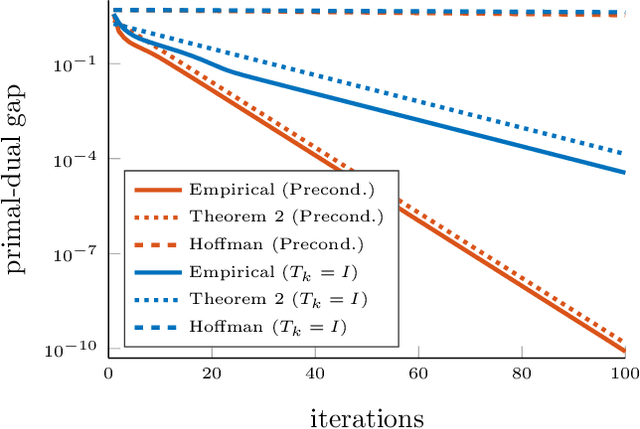
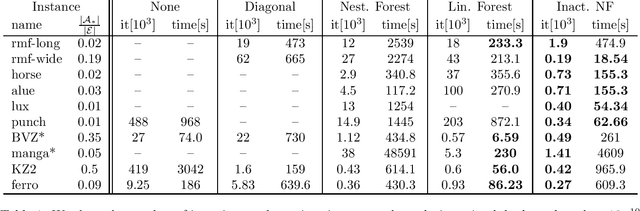
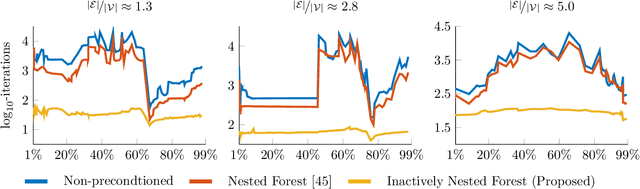
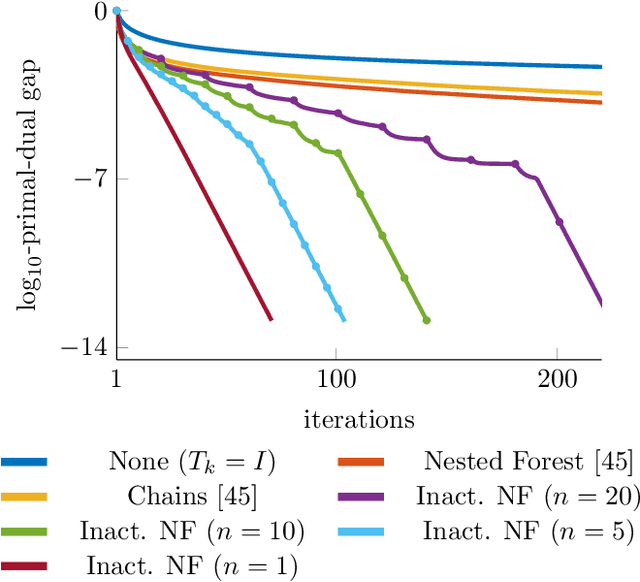
Structured convex optimization on weighted graphs finds numerous applications in machine learning and computer vision. In this work, we propose a novel adaptive preconditioning strategy for proximal algorithms on this problem class. Our preconditioner is driven by a sharp analysis of the local linear convergence rate depending on the "active set" at the current iterate. We show that nested-forest decomposition of the inactive edges yields a guaranteed local linear convergence rate. Further, we propose a practical greedy heuristic which realizes such nested decompositions and show in several numerical experiments that our reconditioning strategy, when applied to proximal gradient or primal-dual hybrid gradient algorithm, achieves competitive performances. Our results suggest that local convergence analysis can serve as a guideline for selecting variable metrics in proximal algorithms.

Learn to Predict Sets Using Feed-Forward Neural Networks

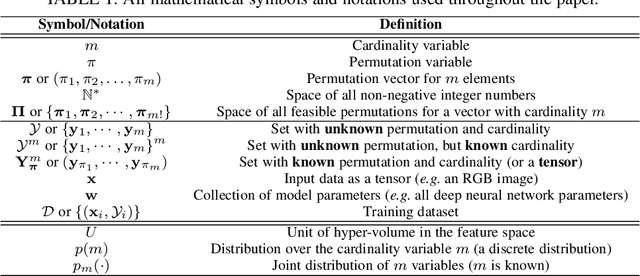
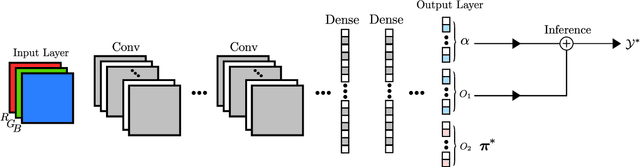
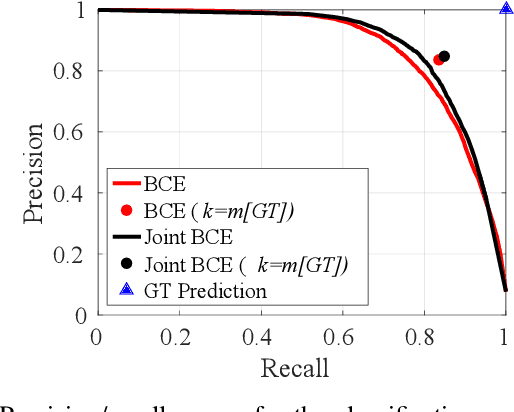
This paper addresses the task of set prediction using deep feed-forward neural networks. A set is a collection of elements which is invariant under permutation and the size of a set is not fixed in advance. Many real-world problems, such as image tagging and object detection, have outputs that are naturally expressed as sets of entities. This creates a challenge for traditional deep neural networks which naturally deal with structured outputs such as vectors, matrices or tensors. We present a novel approach for learning to predict sets with unknown permutation and cardinality using deep neural networks. In our formulation we define a likelihood for a set distribution represented by a) two discrete distributions defining the set cardinally and permutation variables, and b) a joint distribution over set elements with a fixed cardinality. Depending on the problem under consideration, we define different training models for set prediction using deep neural networks. We demonstrate the validity of our set formulations on relevant vision problems such as: 1)multi-label image classification where we achieve state-of-the-art performance on the PASCAL VOC and MS COCO datasets, 2) object detection, for which our formulation outperforms state-of-the-art detectors such as Faster R-CNN and YOLO v3, and 3) a complex CAPTCHA test, where we observe that, surprisingly, our set-based network acquired the ability of mimicking arithmetics without any rules being coded.

From Planes to Corners: Multi-Purpose Primitive Detection in Unorganized 3D Point Clouds

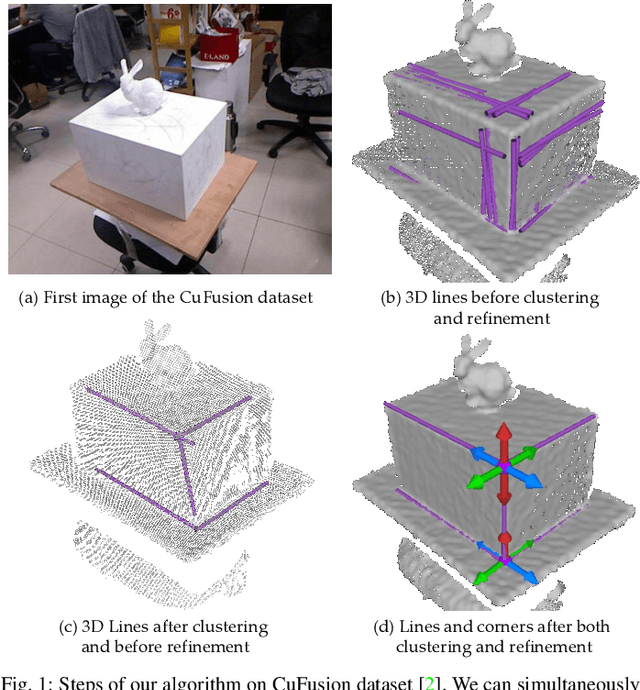
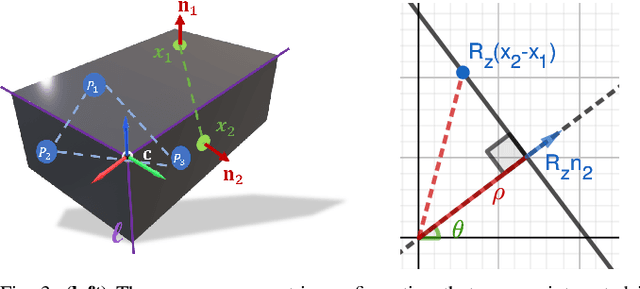
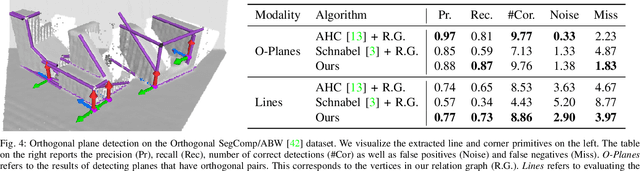
We propose a new method for segmentation-free joint estimation of orthogonal planes, their intersection lines, relationship graph and corners lying at the intersection of three orthogonal planes. Such unified scene exploration under orthogonality allows for multitudes of applications such as semantic plane detection or local and global scan alignment, which in turn can aid robot localization or grasping tasks. Our two-stage pipeline involves a rough yet joint estimation of orthogonal planes followed by a subsequent joint refinement of plane parameters respecting their orthogonality relations. We form a graph of these primitives, paving the way to the extraction of further reliable features: lines and corners. Our experiments demonstrate the validity of our approach in numerous scenarios from wall detection to 6D tracking, both on synthetic and real data.

Inferring Super-Resolution Depth from a Moving Light-Source Enhanced RGB-D Sensor: A Variational Approach

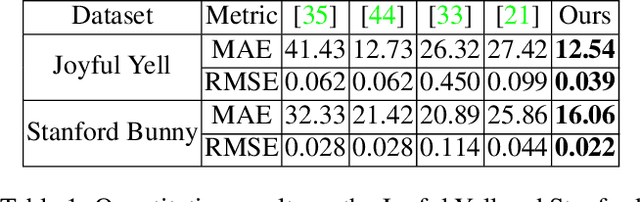
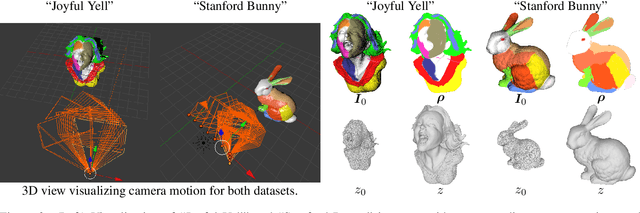
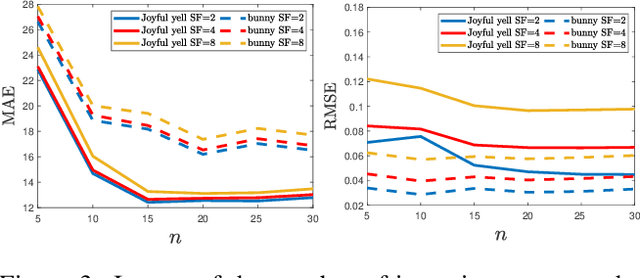
A novel approach towards depth map super-resolution using multi-view uncalibrated photometric stereo is presented. Practically, an LED light source is attached to a commodity RGB-D sensor and is used to capture objects from multiple viewpoints with unknown motion. This non-static camera-to-object setup is described with a nonconvex variational approach such that no calibration on lighting or camera motion is required due to the formulation of an end-to-end joint optimization problem. Solving the proposed variational model results in high resolution depth, reflectance and camera pose estimates, as we show on challenging synthetic and real-world datasets.

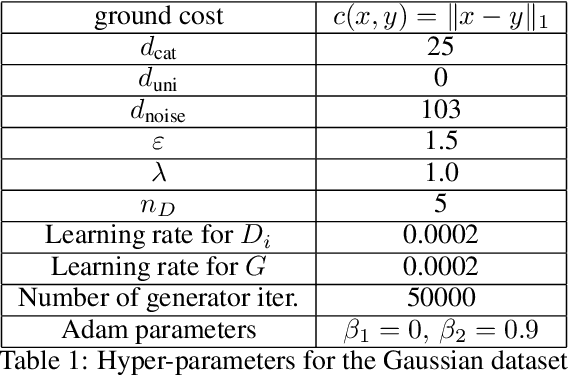
Informative GANs via Structured Regularization of Optimal Transport

We tackle the challenge of disentangled representation learning in generative adversarial networks (GANs) from the perspective of regularized optimal transport (OT). Specifically, a smoothed OT loss gives rise to an implicit transportation plan between the latent space and the data space. Based on this theoretical observation, we exploit a structured regularization on the transportation plan to encourage a prescribed latent subspace to be informative. This yields the formulation of a novel informative OT-based GAN. By convex duality, we obtain the equivalent view that this leads to perturbed ground costs favoring sparsity in the informative latent dimensions. Practically, we devise a stable training algorithm for the proposed informative GAN. Our experiments support the hypothesis that such regularizations effectively yield the discovery of disentangled and interpretable latent representations. Our work showcases potential power of a regularized OT framework in the context of generative modeling through its access to the transport plan. Further challenges are addressed in this line.

Efficient Derivative Computation for Cumulative B-Splines on Lie Groups

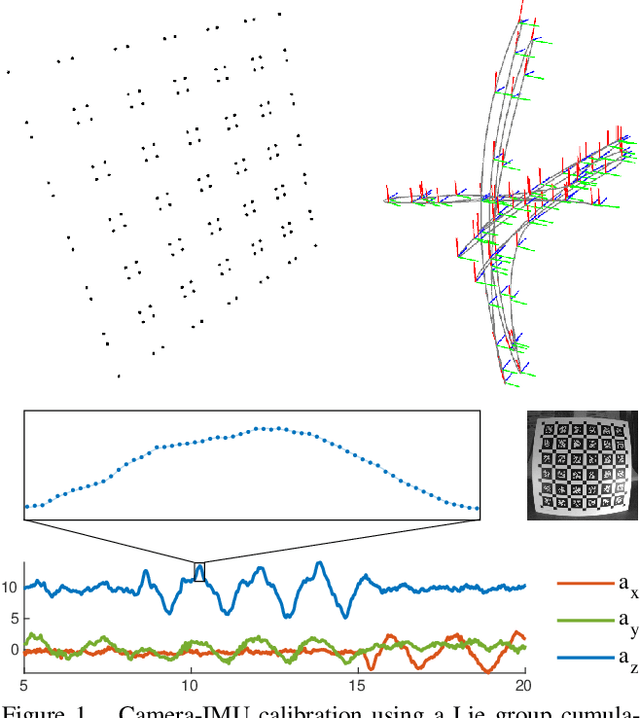
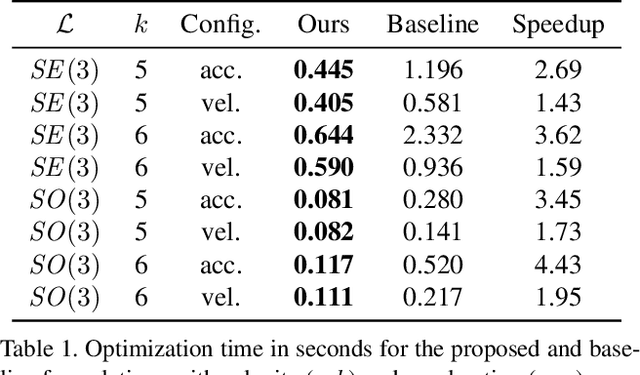
Continuous-time trajectory representation has recently gained popularity for tasks where the fusion of high-frame-rate sensors and multiple unsynchronized devices is required. Lie group cumulative B-splines are a popular way of representing continuous trajectories without singularities. They have been used in near real-time SLAM and odometry systems with IMU, LiDAR, regular, RGB-D and event cameras, as well as for offline calibration. These applications require efficient computation of time derivatives (velocity, acceleration), but all prior works rely on a computationally suboptimal formulation. In this work we present an alternative derivation of time derivatives based on recurrence relations that needs $\mathcal{O}(k)$ instead of $\mathcal{O}(k^2)$ matrix operations (for a spline of order $k$) and results in simple and elegant expressions. While producing the same result, the proposed approach significantly speeds up the trajectory optimization and allows for computing simple analytic derivatives with respect to spline knots. The results presented in this paper pave the way for incorporating continuous-time trajectory representations into more applications where real-time performance is required.

On the well-posedness of uncalibrated photometric stereo under general lighting

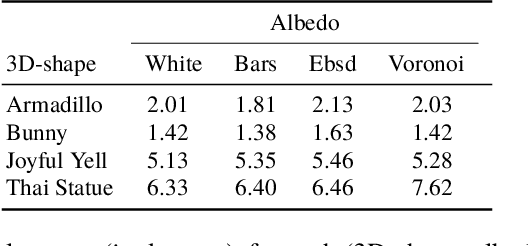
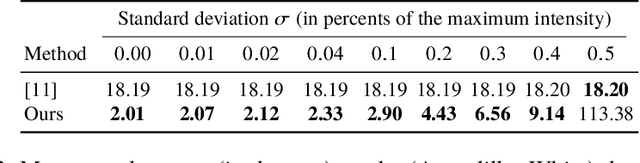
Uncalibrated photometric stereo aims at estimating the 3D-shape of a surface, given a set of images captured from the same viewing angle, but under unknown, varying illumination. While the theoretical foundations of this inverse problem under directional lighting are well-established, there is a lack of mathematical evidence for the uniqueness of a solution under general lighting. On the other hand, stable and accurate heuristical solutions of uncalibrated photometric stereo under such general lighting have recently been proposed. The quality of the results demonstrated therein tends to indicate that the problem may actually be well-posed, but this still has to be established. The present paper addresses this theoretical issue, considering first-order spherical harmonics approximation of general lighting. Two important theoretical results are established. First, the orthographic integrability constraint ensures uniqueness of a solution up to a global concave-convex ambiguity, which had already been conjectured, yet not proven. Second, the perspective integrability constraint makes the problem well-posed, which generalizes a previous result limited to directional lighting. Eventually, a closed-form expression for the unique least-squares solution of the problem under perspective projection is provided, allowing numerical simulations on synthetic data to empirically validate our findings.

Rolling-Shutter Modelling for Direct Visual-Inertial Odometry

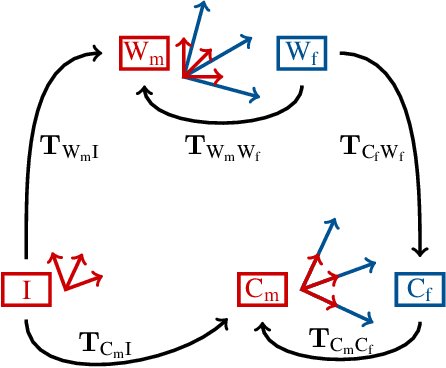
We present a direct visual-inertial odometry (VIO) method which estimates the motion of the sensor setup and sparse 3D geometry of the environment based on measurements from a rolling-shutter camera and an inertial measurement unit (IMU). The visual part of the system performs a photometric bundle adjustment on a sparse set of points. This direct approach does not extract feature points and is able to track not only corners, but any pixels with sufficient gradient magnitude. Neglecting rolling-shutter effects in the visual part severely degrades accuracy and robustness of the system. In this paper, we incorporate a rolling-shutter model into the photometric bundle adjustment that estimates a set of recent keyframe poses and the inverse depth of a sparse set of points. IMU information is accumulated between several frames using measurement preintegration, and is inserted into the optimization as an additional constraint between selected keyframes. For every keyframe we estimate not only the pose but also velocity and biases to correct the IMU measurements. Unlike systems with global-shutter cameras, we use both IMU measurements and rolling-shutter effects of the camera to estimate velocity and biases for every state. Last, we evaluate our system on a novel dataset that contains global-shutter and rolling-shutter images, IMU data and ground-truth poses for ten different sequences, which we make publicly available. Evaluation shows that the proposed method outperforms a system where rolling shutter is not modelled and achieves similar accuracy to the global-shutter method on global-shutter data.

Deep Learning for 2D and 3D Rotatable Data: An Overview of Methods

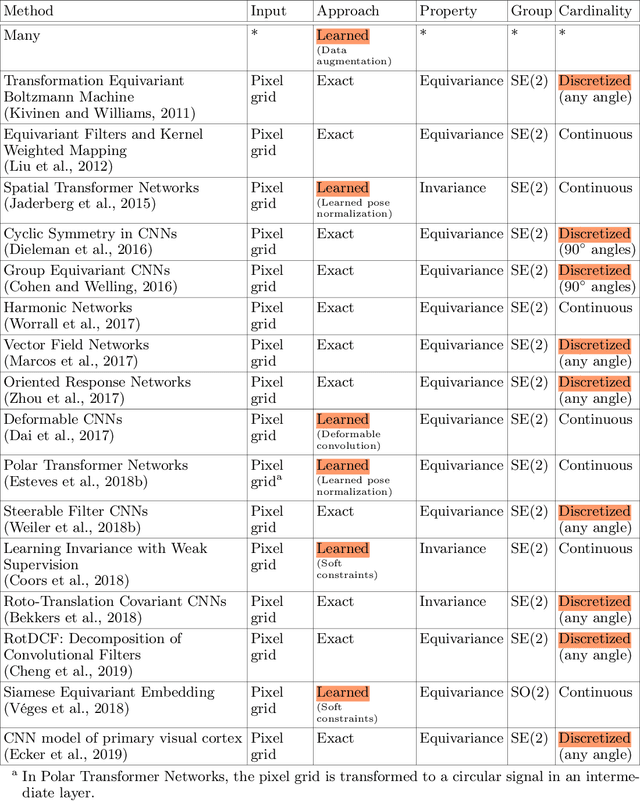
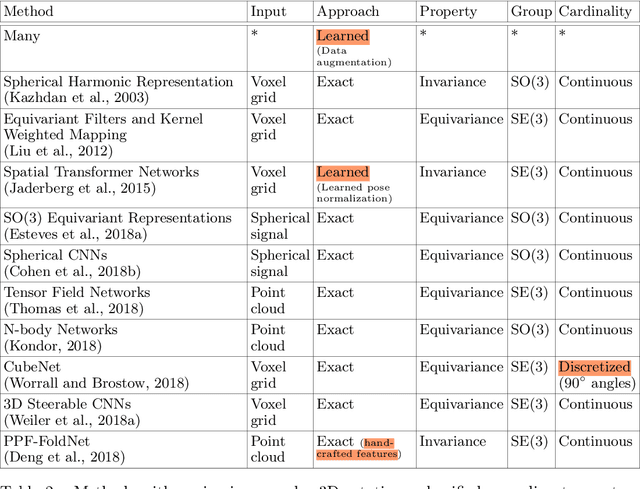
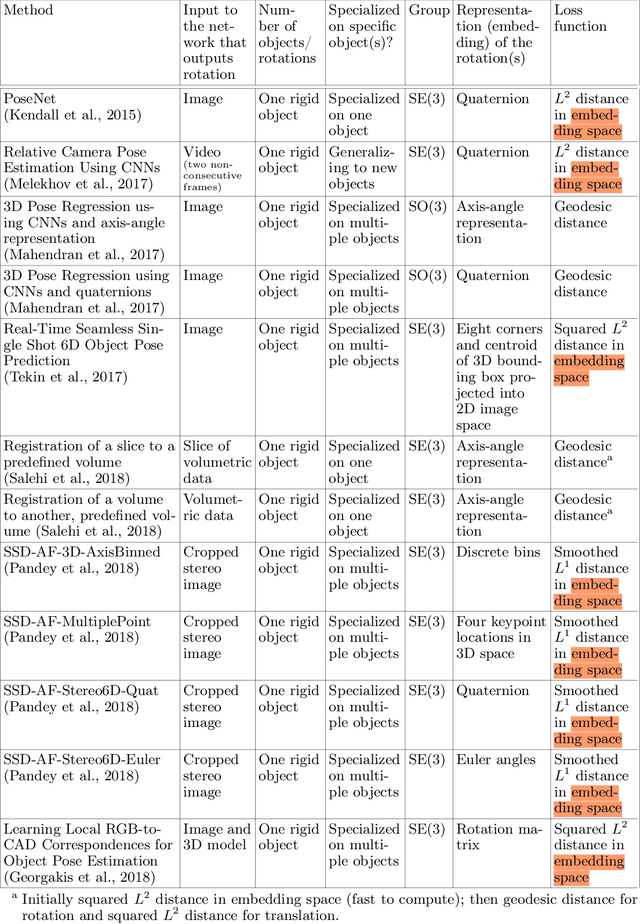
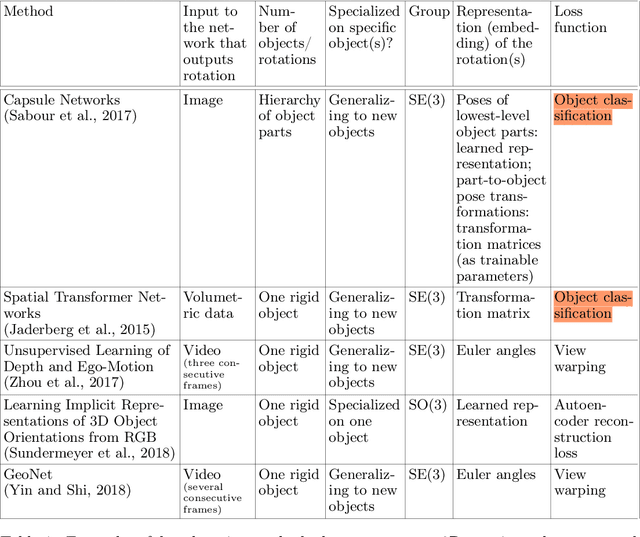
One of the reasons for the success of convolutional networks is their equivariance/invariance under translations. However, rotatable data such as molecules, living cells, everyday objects, or galaxies require processing with equivariance/invariance under rotations in cases where the rotation of the coordinate system does not affect the meaning of the data (e.g. object classification). On the other hand, estimation/processing of rotations is necessary in cases where rotations are important (e.g. motion estimation). There has been recent progress in methods and theory in all these regards. Here we provide an overview of existing methods, both for 2D and 3D rotations (and translations), and identify commonalities and links between them, in the hope that our insights will be useful for choosing and perfecting the methods.