Linear time small coresets for k-mean clustering of segments with applications

We study the $k$-means problem for a set $\mathcal{S} \subseteq \mathbb{R}^d$ of $n$ segments, aiming to find $k$ centers $X \subseteq \mathbb{R}^d$ that minimize $D(\mathcal{S},X) := \sum_{S \in \mathcal{S}} \min_{x \in X} D(S,x)$, where $D(S,x) := \int_{p \in S} |p - x| dp$ measures the total distance from each point along a segment to a center. Variants of this problem include handling outliers, employing alternative distance functions such as M-estimators, weighting distances to achieve balanced clustering, or enforcing unique cluster assignments. For any $\varepsilon > 0$, an $\varepsilon$-coreset is a weighted subset $C \subseteq \mathbb{R}^d$ that approximates $D(\mathcal{S},X)$ within a factor of $1 \pm \varepsilon$ for any set of $k$ centers, enabling efficient streaming, distributed, or parallel computation. We propose the first coreset construction that provably handles arbitrary input segments. For constant $k$ and $\varepsilon$, it produces a coreset of size $O(\log^2 n)$ computable in $O(nd)$ time. Experiments, including a real-time video tracking application, demonstrate substantial speedups with minimal loss in clustering accuracy, confirming both the practical efficiency and theoretical guarantees of our method.

Provable Imbalanced Point Clustering

We suggest efficient and provable methods to compute an approximation for imbalanced point clustering, that is, fitting $k$-centers to a set of points in $\mathbb{R}^d$, for any $d,k\geq 1$. To this end, we utilize \emph{coresets}, which, in the context of the paper, are essentially weighted sets of points in $\mathbb{R}^d$ that approximate the fitting loss for every model in a given set, up to a multiplicative factor of $1\pm\varepsilon$. We provide [Section 3 and Section E in the appendix] experiments that show the empirical contribution of our suggested methods for real images (novel and reference), synthetic data, and real-world data. We also propose choice clustering, which by combining clustering algorithms yields better performance than each one separately.

Opinion Spam Detection: A New Approach Using Machine Learning and Network-Based Algorithms

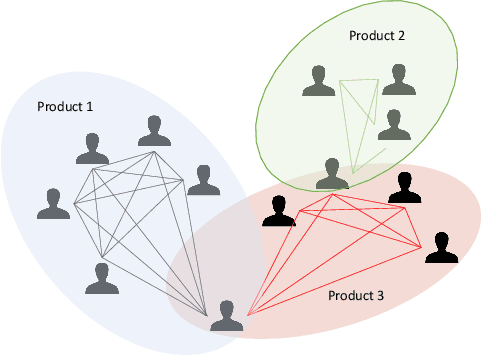
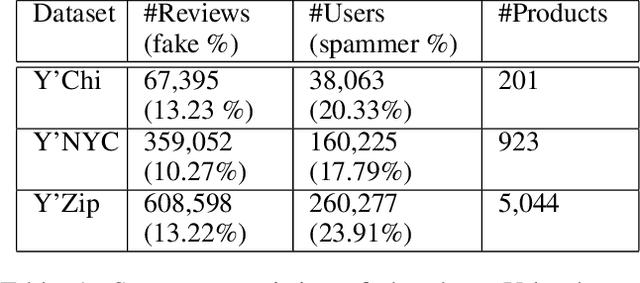
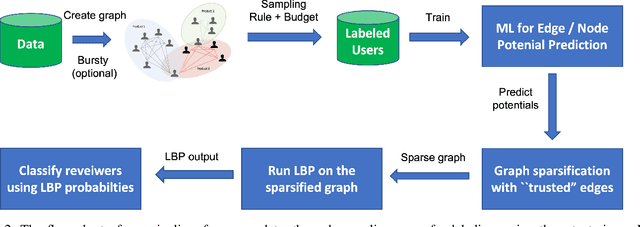
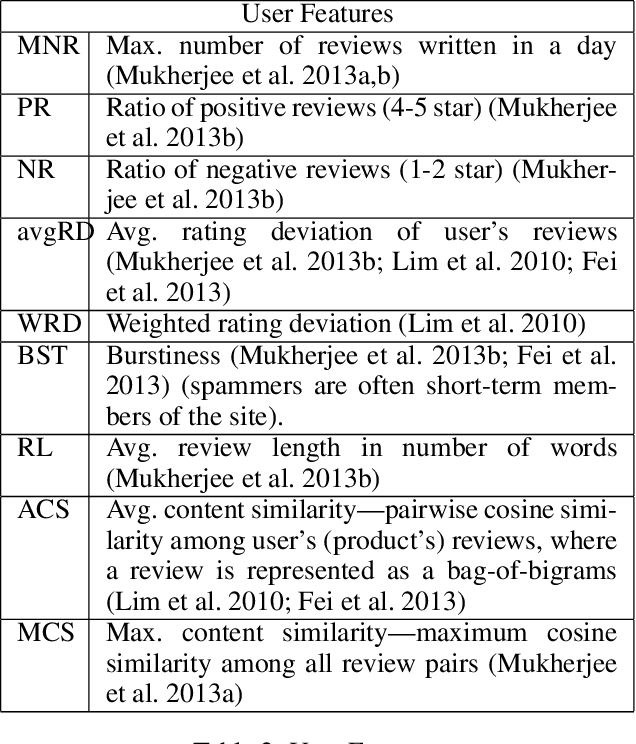
E-commerce is the fastest-growing segment of the economy. Online reviews play a crucial role in helping consumers evaluate and compare products and services. As a result, fake reviews (opinion spam) are becoming more prevalent and negatively impacting customers and service providers. There are many reasons why it is hard to identify opinion spammers automatically, including the absence of reliable labeled data. This limitation precludes an off-the-shelf application of a machine learning pipeline. We propose a new method for classifying reviewers as spammers or benign, combining machine learning with a message-passing algorithm that capitalizes on the users' graph structure to compensate for the possible scarcity of labeled data. We devise a new way of sampling the labels for the training step (active learning), replacing the typical uniform sampling. Experiments on three large real-world datasets from Yelp.com show that our method outperforms state-of-the-art active learning approaches and also machine learning methods that use a much larger set of labeled data for training.