Cynthia Dwork
Interpreting Robust Optimization via Adversarial Influence Functions
Oct 03, 2020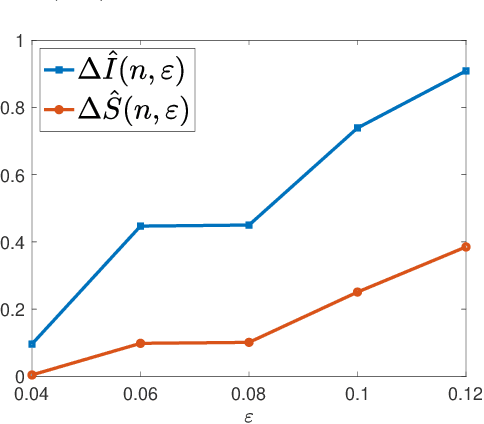
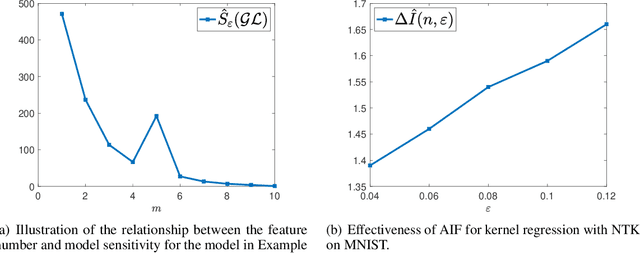
Abstract:Robust optimization has been widely used in nowadays data science, especially in adversarial training. However, little research has been done to quantify how robust optimization changes the optimizers and the prediction losses comparing to standard training. In this paper, inspired by the influence function in robust statistics, we introduce the Adversarial Influence Function (AIF) as a tool to investigate the solution produced by robust optimization. The proposed AIF enjoys a closed-form and can be calculated efficiently. To illustrate the usage of AIF, we apply it to study model sensitivity -- a quantity defined to capture the change of prediction losses on the natural data after implementing robust optimization. We use AIF to analyze how model complexity and randomized smoothing affect the model sensitivity with respect to specific models. We further derive AIF for kernel regressions, with a particular application to neural tangent kernels, and experimentally demonstrate the effectiveness of the proposed AIF. Lastly, the theories of AIF will be extended to distributional robust optimization.
Private Post-GAN Boosting
Jul 23, 2020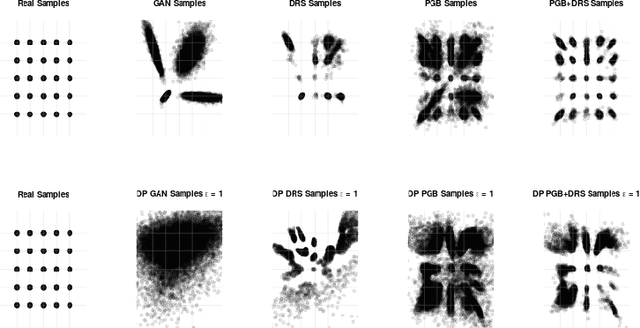
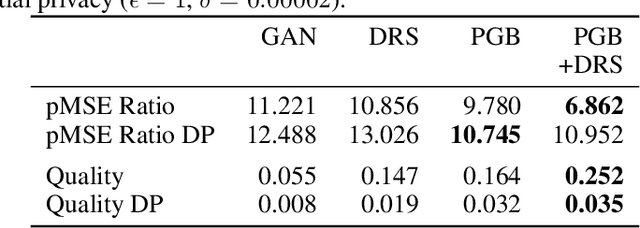
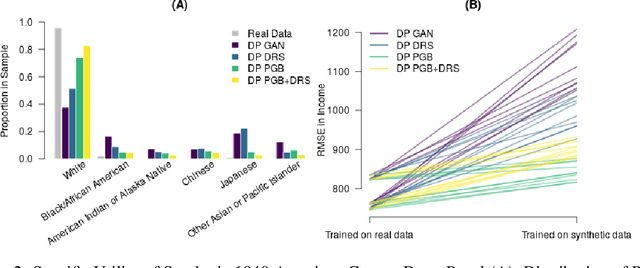
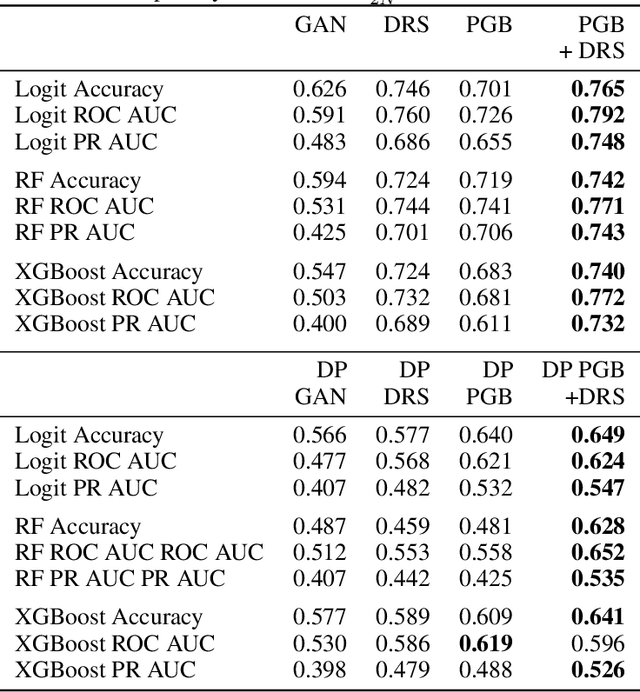
Abstract:Differentially private GANs have proven to be a promising approach for generating realistic synthetic data without compromising the privacy of individuals. However, due to the privacy-protective noise introduced in the training, the convergence of GANs becomes even more elusive, which often leads to poor utility in the output generator at the end of training. We propose Private post-GAN boosting (Private PGB), a differentially private method that combines samples produced by the sequence of generators obtained during GAN training to create a high-quality synthetic dataset. Our method leverages the Private Multiplicative Weights method (Hardt and Rothblum, 2010) and the discriminator rejection sampling technique (Azadi et al., 2019) for reweighting generated samples, to obtain high quality synthetic data even in cases where GAN training does not converge. We evaluate Private PGB on a Gaussian mixture dataset and two US Census datasets, and demonstrate that Private PGB improves upon the standard private GAN approach across a collection of quality measures. Finally, we provide a non-private variant of PGB that improves the data quality of standard GAN training.
Representation via Representations: Domain Generalization via Adversarially Learned Invariant Representations
Jun 20, 2020


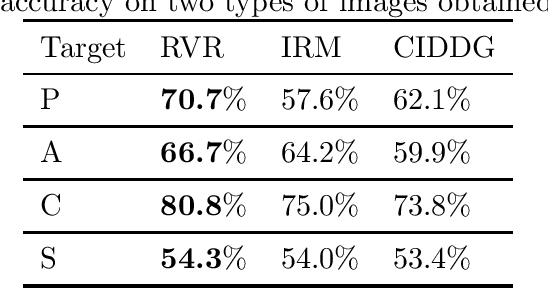
Abstract:We investigate the power of censoring techniques, first developed for learning {\em fair representations}, to address domain generalization. We examine {\em adversarial} censoring techniques for learning invariant representations from multiple "studies" (or domains), where each study is drawn according to a distribution on domains. The mapping is used at test time to classify instances from a new domain. In many contexts, such as medical forecasting, domain generalization from studies in populous areas (where data are plentiful), to geographically remote populations (for which no training data exist) provides fairness of a different flavor, not anticipated in previous work on algorithmic fairness. We study an adversarial loss function for $k$ domains and precisely characterize its limiting behavior as $k$ grows, formalizing and proving the intuition, backed by experiments, that observing data from a larger number of domains helps. The limiting results are accompanied by non-asymptotic learning-theoretic bounds. Furthermore, we obtain sufficient conditions for good worst-case prediction performance of our algorithm on previously unseen domains. Finally, we decompose our mappings into two components and provide a complete characterization of invariance in terms of this decomposition. To our knowledge, our results provide the first formal guarantees of these kinds for adversarial invariant domain generalization.
Individual Fairness in Pipelines
Apr 12, 2020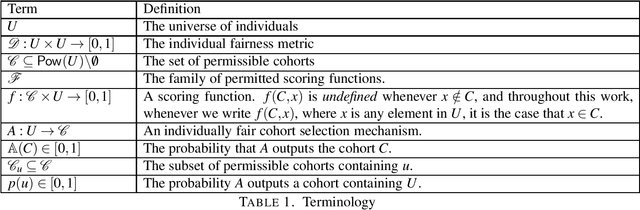

Abstract:It is well understood that a system built from individually fair components may not itself be individually fair. In this work, we investigate individual fairness under pipeline composition. Pipelines differ from ordinary sequential or repeated composition in that individuals may drop out at any stage, and classification in subsequent stages may depend on the remaining "cohort" of individuals. As an example, a company might hire a team for a new project and at a later point promote the highest performer on the team. Unlike other repeated classification settings, where the degree of unfairness degrades gracefully over multiple fair steps, the degree of unfairness in pipelines can be arbitrary, even in a pipeline with just two stages. Guided by a panoply of real-world examples, we provide a rigorous framework for evaluating different types of fairness guarantees for pipelines. We show that na\"{i}ve auditing is unable to uncover systematic unfairness and that, in order to ensure fairness, some form of dependence must exist between the design of algorithms at different stages in the pipeline. Finally, we provide constructions that permit flexibility at later stages, meaning that there is no need to lock in the entire pipeline at the time that the early stage is constructed.
Abstracting Fairness: Oracles, Metrics, and Interpretability
Apr 04, 2020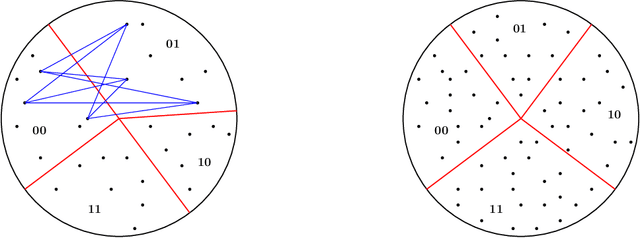
Abstract:It is well understood that classification algorithms, for example, for deciding on loan applications, cannot be evaluated for fairness without taking context into account. We examine what can be learned from a fairness oracle equipped with an underlying understanding of ``true'' fairness. The oracle takes as input a (context, classifier) pair satisfying an arbitrary fairness definition, and accepts or rejects the pair according to whether the classifier satisfies the underlying fairness truth. Our principal conceptual result is an extraction procedure that learns the underlying truth; moreover, the procedure can learn an approximation to this truth given access to a weak form of the oracle. Since every ``truly fair'' classifier induces a coarse metric, in which those receiving the same decision are at distance zero from one another and those receiving different decisions are at distance one, this extraction process provides the basis for ensuring a rough form of metric fairness, also known as individual fairness. Our principal technical result is a higher fidelity extractor under a mild technical constraint on the weak oracle's conception of fairness. Our framework permits the scenario in which many classifiers, with differing outcomes, may all be considered fair. Our results have implications for interpretablity -- a highly desired but poorly defined property of classification systems that endeavors to permit a human arbiter to reject classifiers deemed to be ``unfair'' or illegitimately derived.
Architecture Selection via the Trade-off Between Accuracy and Robustness
Jun 04, 2019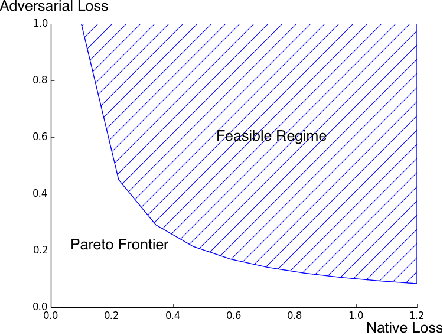
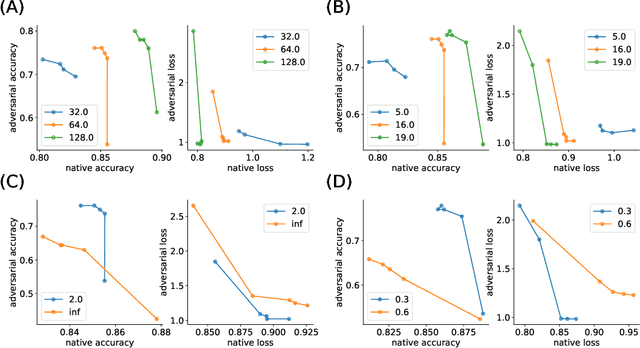
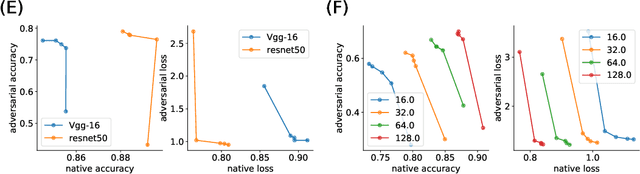
Abstract:We provide a general framework for characterizing the trade-off between accuracy and robustness in supervised learning. We propose a method and define quantities to characterize the trade-off between accuracy and robustness for a given architecture, and provide theoretical insight into the trade-off. Specifically we introduce a simple trade-off curve, define and study an influence function that captures the sensitivity, under adversarial attack, of the optima of a given loss function. We further show how adversarial training regularizes the parameters in an over-parameterized linear model, recovering the LASSO and ridge regression as special cases, which also allows us to theoretically analyze the behavior of the trade-off curve. In experiments, we demonstrate the corresponding trade-off curves of neural networks and how they vary with respect to factors such as number of layers, neurons, and across different network structures. Such information provides a useful guideline to architecture selection.
Differentially Private False Discovery Rate Control
Jul 11, 2018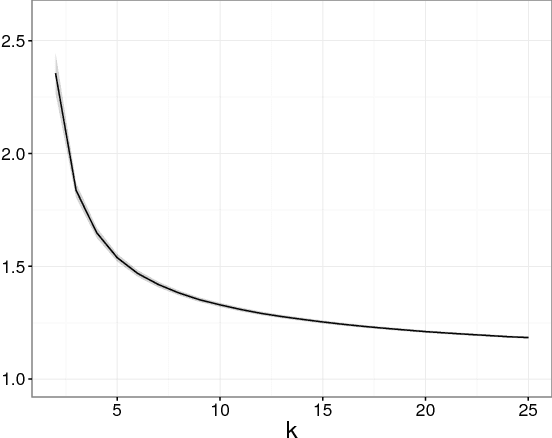
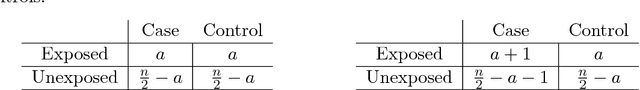
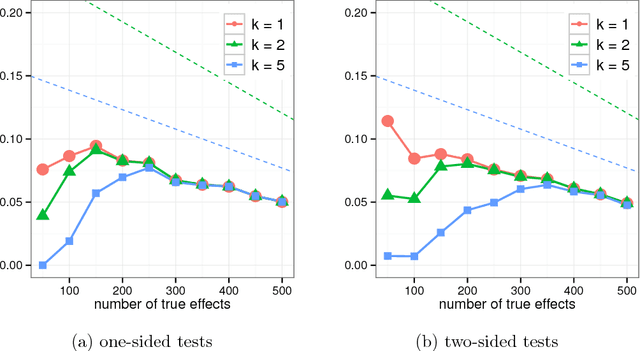
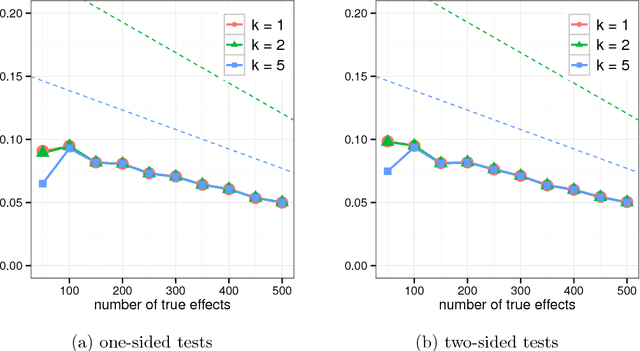
Abstract:Differential privacy provides a rigorous framework for privacy-preserving data analysis. This paper proposes the first differentially private procedure for controlling the false discovery rate (FDR) in multiple hypothesis testing. Inspired by the Benjamini- Hochberg procedure (BHq), our approach is to first repeatedly add noise to the logarithms of the p-values to ensure differential privacy and to select an approximately smallest p-value serving as a promising candidate at each iteration; the selected p-values are further supplied to the BHq and our private procedure releases only the rejected ones. Apart from the privacy considerations, we develop a new technique that is based on a backward submartingale for proving FDR control of a broad class of multiple testing procedures, including our private procedure, and both the BHq step-up and step-down procedures. As a novel aspect, the proof works for arbitrary dependence between the true null and false null test statistics, while FDR control is maintained up to a small multiplicative factor. This theoretical guarantee is the first in the FDR literature to explain the empirical validity of the BHq procedure in three simulation studies.
Fairness Under Composition
Jun 15, 2018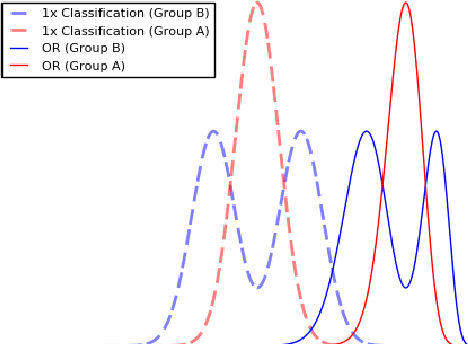
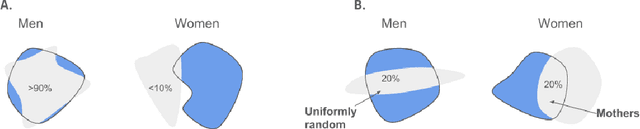
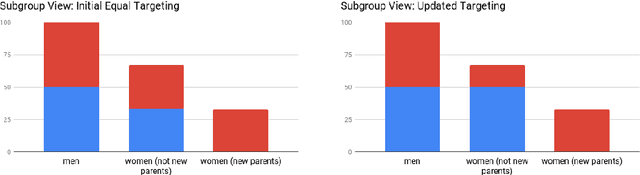
Abstract:Much of the literature on fair classifiers considers the case of a single classifier used once, in isolation. We initiate the study of composition of fair classifiers. In particular, we address the pitfalls of na{\i}ve composition and give general constructions for fair composition. Focusing on the individual fairness setting proposed in [Dwork, Hardt, Pitassi, Reingold, Zemel, 2011], we also extend our results to a large class of group fairness definitions popular in the recent literature. We exhibit several cases in which group fairness definitions give misleading signals under composition and conclude that additional context is needed to evaluate both group and individual fairness under composition.
Privacy-preserving Prediction
May 09, 2018
Abstract:Ensuring differential privacy of models learned from sensitive user data is an important goal that has been studied extensively in recent years. It is now known that for some basic learning problems, especially those involving high-dimensional data, producing an accurate private model requires much more data than learning without privacy. At the same time, in many applications it is not necessary to expose the model itself. Instead users may be allowed to query the prediction model on their inputs only through an appropriate interface. Here we formulate the problem of ensuring privacy of individual predictions and investigate the overheads required to achieve it in several standard models of classification and regression. We first describe a simple baseline approach based on training several models on disjoint subsets of data and using standard private aggregation techniques to predict. We show that this approach has nearly optimal sample complexity for (realizable) PAC learning of any class of Boolean functions. At the same time, without strong assumptions on the data distribution, the aggregation step introduces a substantial overhead. We demonstrate that this overhead can be avoided for the well-studied class of thresholds on a line and for a number of standard settings of convex regression. The analysis of our algorithm for learning thresholds relies crucially on strong generalization guarantees that we establish for all differentially private prediction algorithms.
Decoupled classifiers for fair and efficient machine learning
Jul 20, 2017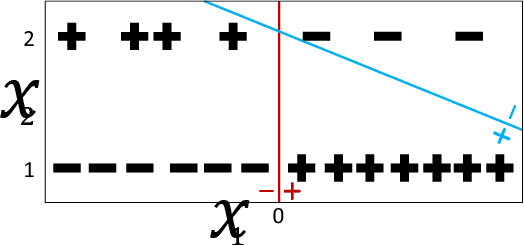
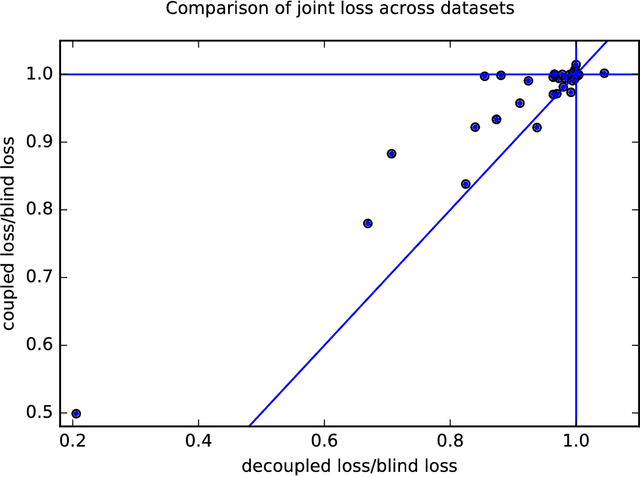
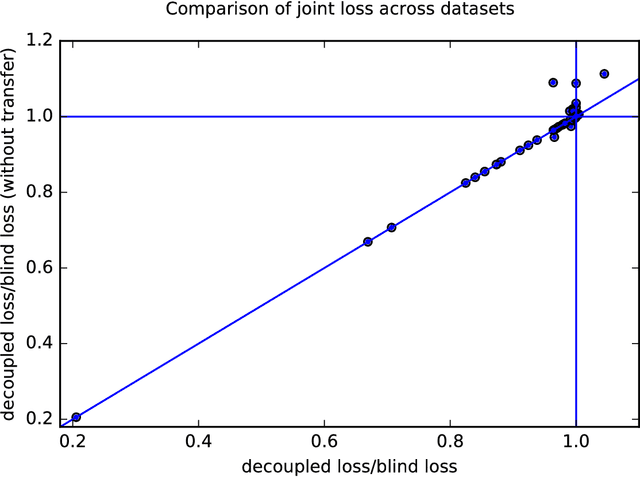
Abstract:When it is ethical and legal to use a sensitive attribute (such as gender or race) in machine learning systems, the question remains how to do so. We show that the naive application of machine learning algorithms using sensitive features leads to an inherent tradeoff in accuracy between groups. We provide a simple and efficient decoupling technique, that can be added on top of any black-box machine learning algorithm, to learn different classifiers for different groups. Transfer learning is used to mitigate the problem of having too little data on any one group. The method can apply to a range of fairness criteria. In particular, we require the application designer to specify as joint loss function that makes explicit the trade-off between fairness and accuracy. Our reduction is shown to efficiently find the minimum loss as long as the objective has a certain natural monotonicity property which may be of independent interest in the study of fairness in algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge