Linear Regression with Unknown Truncation Beyond Gaussian Features

In truncated linear regression, samples $(x,y)$ are shown only when the outcome $y$ falls inside a certain survival set $S^\star$ and the goal is to estimate the unknown $d$-dimensional regressor $w^\star$. This problem has a long history of study in Statistics and Machine Learning going back to the works of (Galton, 1897; Tobin, 1958) and more recently in, e.g., (Daskalakis et al., 2019; 2021; Lee et al., 2023; 2024). Despite this long history, however, most prior works are limited to the special case where $S^\star$ is precisely known. The more practically relevant case, where $S^\star$ is unknown and must be learned from data, remains open: indeed, here the only available algorithms require strong assumptions on the distribution of the feature vectors (e.g., Gaussianity) and, even then, have a $d^{\mathrm{poly} (1/\varepsilon)}$ run time for achieving $\varepsilon$ accuracy. In this work, we give the first algorithm for truncated linear regression with unknown survival set that runs in $\mathrm{poly} (d/\varepsilon)$ time, by only requiring that the feature vectors are sub-Gaussian. Our algorithm relies on a novel subroutine for efficiently learning unions of a bounded number of intervals using access to positive examples (without any negative examples) under a certain smoothness condition. This learning guarantee adds to the line of works on positive-only PAC learning and may be of independent interest.

EntRGi: Entropy Aware Reward Guidance for Diffusion Language Models

Reward guidance has been applied to great success in the test-time adaptation of continuous diffusion models; it updates each denoising step using the gradients from a downstream reward model. We study reward guidance for discrete diffusion language models, where one cannot differentiate through the natural outputs of the model because they are discrete tokens. Existing approaches either replace these discrete tokens with continuous relaxations, or employ techniques like the straight-through estimator. In this work, we show the downsides of both these methods. The former degrades gradient feedback because the reward model has never been trained with continuous inputs. The latter involves incorrect optimization because the gradient evaluated at discrete tokens is used to update continuous logits. Our key innovation is to go beyond this tradeoff by introducing a novel mechanism called EntRGi: Entropy aware Reward Guidance that dynamically regulates the gradients from the reward model. By modulating the continuous relaxation using the model's confidence, our approach substantially improves reward guidance while providing reliable inputs to the reward model. We empirically validate our approach on a 7B-parameter diffusion language model across 3 diverse reward models and 3 multi-skill benchmarks, showing consistent improvements over state-of-the-art methods.

Succeeding at Scale: Automated Multi-Retriever Fusion and Query-Side Adaptation for Multi-Tenant Search

Large-scale multi-tenant retrieval systems amass vast user query logs yet critically lack the curated relevance labels required for effective domain adaptation. This "dark data" problem is exacerbated by the operational cost of model updates: jointly fine-tuning query and document encoders requires re-indexing the entire corpus, which is prohibitive in multi-tenant environments with thousands of isolated indices. To address these dual challenges, we introduce \textbf{DevRev Search}, a passage retrieval benchmark for technical customer support constructed through a fully automatic pipeline. We employ a \textbf{fusion-based candidate generation} strategy, pooling results from diverse sparse and dense retrievers, and utilize an LLM-as-a-Judge to perform rigorous \textbf{consistency filtering} and relevance assignment. We further propose a practical \textbf{Index-Preserving Adaptation} strategy: by fine-tuning only the query encoder via Low-Rank Adaptation (LoRA), we achieve competitive performance improvements while keeping the document index frozen. Our experiments on DevRev Search and SciFact demonstrate that targeting specific transformer layers in the query encoder yields optimal quality-efficiency trade-offs, offering a scalable path for personalized enterprise search.

Test-Time Anchoring for Discrete Diffusion Posterior Sampling

We study the problem of posterior sampling using pretrained discrete diffusion foundation models, aiming to recover images from noisy measurements without retraining task-specific models. While diffusion models have achieved remarkable success in generative modeling, most advances rely on continuous Gaussian diffusion. In contrast, discrete diffusion offers a unified framework for jointly modeling categorical data such as text and images. Beyond unification, discrete diffusion provides faster inference, finer control, and principled training-free Bayesian inference, making it particularly well-suited for posterior sampling. However, existing approaches to discrete diffusion posterior sampling face severe challenges: derivative-free guidance yields sparse signals, continuous relaxations limit applicability, and split Gibbs samplers suffer from the curse of dimensionality. To overcome these limitations, we introduce Anchored Posterior Sampling (APS) for masked diffusion foundation models, built on two key innovations -- quantized expectation for gradient-like guidance in discrete embedding space, and anchored remasking for adaptive decoding. Our approach achieves state-of-the-art performance among discrete diffusion samplers across linear and nonlinear inverse problems on the standard benchmarks. We further demonstrate the benefits of our approach in training-free stylization and text-guided editing.

Anchored Diffusion Language Model

Diffusion Language Models (DLMs) promise parallel generation and bidirectional context, yet they underperform autoregressive (AR) models in both likelihood modeling and generated text quality. We identify that this performance gap arises when important tokens (e.g., key words or low-frequency words that anchor a sentence) are masked early in the forward process, limiting contextual information for accurate reconstruction. To address this, we introduce the Anchored Diffusion Language Model (ADLM), a novel two-stage framework that first predicts distributions over important tokens via an anchor network, and then predicts the likelihoods of missing tokens conditioned on the anchored predictions. ADLM significantly improves test perplexity on LM1B and OpenWebText, achieving up to 25.4% gains over prior DLMs, and narrows the gap with strong AR baselines. It also achieves state-of-the-art performance in zero-shot generalization across seven benchmarks and surpasses AR models in MAUVE score, which marks the first time a DLM generates better human-like text than an AR model. Theoretically, we derive an Anchored Negative Evidence Lower Bound (ANELBO) objective and show that anchoring improves sample complexity and likelihood modeling. Beyond diffusion, anchoring boosts performance in AR models and enhances reasoning in math and logic tasks, outperforming existing chain-of-thought approaches

Asymptotically-Optimal Gaussian Bandits with Side Observations

We study the problem of Gaussian bandits with general side information, as first introduced by Wu, Szepesvari, and Gyorgy. In this setting, the play of an arm reveals information about other arms, according to an arbitrary a priori known side information matrix: each element of this matrix encodes the fidelity of the information that the ``row'' arm reveals about the ``column'' arm. In the case of Gaussian noise, this model subsumes standard bandits, full-feedback, and graph-structured feedback as special cases. In this work, we first construct an LP-based asymptotic instance-dependent lower bound on the regret. The LP optimizes the cost (regret) required to reliably estimate the suboptimality gap of each arm. This LP lower bound motivates our main contribution: the first known asymptotically optimal algorithm for this general setting.

On Mitigating Affinity Bias through Bandits with Evolving Biased Feedback

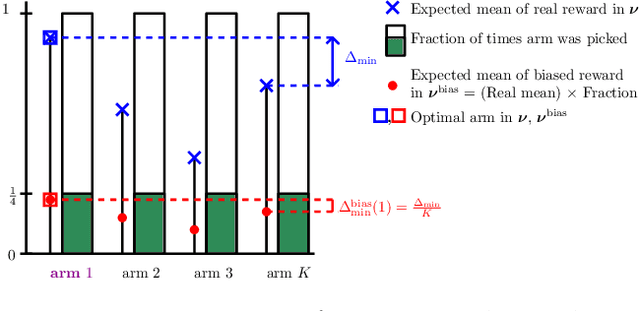
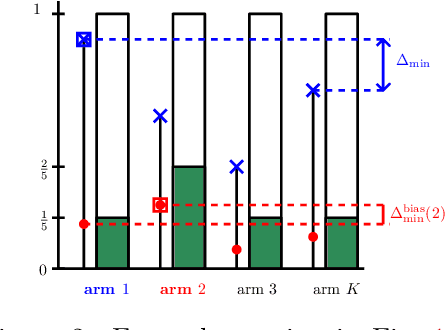
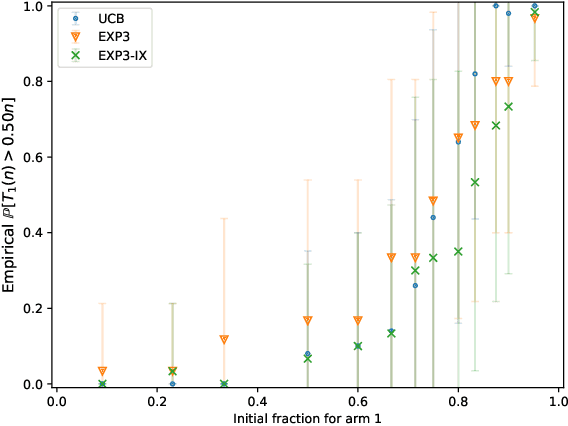
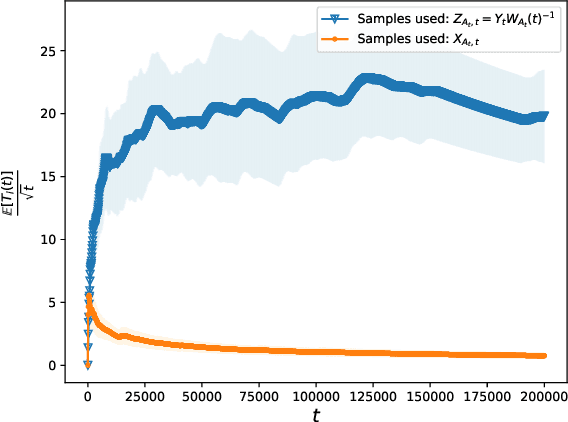
Unconscious bias has been shown to influence how we assess our peers, with consequences for hiring, promotions and admissions. In this work, we focus on affinity bias, the component of unconscious bias which leads us to prefer people who are similar to us, despite no deliberate intention of favoritism. In a world where the people hired today become part of the hiring committee of tomorrow, we are particularly interested in understanding (and mitigating) how affinity bias affects this feedback loop. This problem has two distinctive features: 1) we only observe the biased value of a candidate, but we want to optimize with respect to their real value 2) the bias towards a candidate with a specific set of traits depends on the fraction of people in the hiring committee with the same set of traits. We introduce a new bandits variant that exhibits those two features, which we call affinity bandits. Unsurprisingly, classical algorithms such as UCB often fail to identify the best arm in this setting. We prove a new instance-dependent regret lower bound, which is larger than that in the standard bandit setting by a multiplicative function of $K$. Since we treat rewards that are time-varying and dependent on the policy's past actions, deriving this lower bound requires developing proof techniques beyond the standard bandit techniques. Finally, we design an elimination-style algorithm which nearly matches this regret, despite never observing the real rewards.

Optimization Can Learn Johnson Lindenstrauss Embeddings

Embeddings play a pivotal role across various disciplines, offering compact representations of complex data structures. Randomized methods like Johnson-Lindenstrauss (JL) provide state-of-the-art and essentially unimprovable theoretical guarantees for achieving such representations. These guarantees are worst-case and in particular, neither the analysis, nor the algorithm, takes into account any potential structural information of the data. The natural question is: must we randomize? Could we instead use an optimization-based approach, working directly with the data? A first answer is no: as we show, the distance-preserving objective of JL has a non-convex landscape over the space of projection matrices, with many bad stationary points. But this is not the final answer. We present a novel method motivated by diffusion models, that circumvents this fundamental challenge: rather than performing optimization directly over the space of projection matrices, we use optimization over the larger space of random solution samplers, gradually reducing the variance of the sampler. We show that by moving through this larger space, our objective converges to a deterministic (zero variance) solution, avoiding bad stationary points. This method can also be seen as an optimization-based derandomization approach and is an idea and method that we believe can be applied to many other problems.

Semantic Image Inversion and Editing using Rectified Stochastic Differential Equations

Generative models transform random noise into images; their inversion aims to transform images back to structured noise for recovery and editing. This paper addresses two key tasks: (i) inversion and (ii) editing of a real image using stochastic equivalents of rectified flow models (such as Flux). Although Diffusion Models (DMs) have recently dominated the field of generative modeling for images, their inversion presents faithfulness and editability challenges due to nonlinearities in drift and diffusion. Existing state-of-the-art DM inversion approaches rely on training of additional parameters or test-time optimization of latent variables; both are expensive in practice. Rectified Flows (RFs) offer a promising alternative to diffusion models, yet their inversion has been underexplored. We propose RF inversion using dynamic optimal control derived via a linear quadratic regulator. We prove that the resulting vector field is equivalent to a rectified stochastic differential equation. Additionally, we extend our framework to design a stochastic sampler for Flux. Our inversion method allows for state-of-the-art performance in zero-shot inversion and editing, outperforming prior works in stroke-to-image synthesis and semantic image editing, with large-scale human evaluations confirming user preference.

RL in Latent MDPs is Tractable: Online Guarantees via Off-Policy Evaluation

In many real-world decision problems there is partially observed, hidden or latent information that remains fixed throughout an interaction. Such decision problems can be modeled as Latent Markov Decision Processes (LMDPs), where a latent variable is selected at the beginning of an interaction and is not disclosed to the agent. In the last decade, there has been significant progress in solving LMDPs under different structural assumptions. However, for general LMDPs, there is no known learning algorithm that provably matches the existing lower bound~\cite{kwon2021rl}. We introduce the first sample-efficient algorithm for LMDPs without any additional structural assumptions. Our result builds off a new perspective on the role of off-policy evaluation guarantees and coverage coefficients in LMDPs, a perspective, that has been overlooked in the context of exploration in partially observed environments. Specifically, we establish a novel off-policy evaluation lemma and introduce a new coverage coefficient for LMDPs. Then, we show how these can be used to derive near-optimal guarantees of an optimistic exploration algorithm. These results, we believe, can be valuable for a wide range of interactive learning problems beyond LMDPs, and especially, for partially observed environments.