Language Models over Canonical Byte-Pair Encodings

Modern language models represent probability distributions over character strings as distributions over (shorter) token strings derived via a deterministic tokenizer, such as byte-pair encoding. While this approach is highly effective at scaling up language models to large corpora, its current incarnations have a concerning property: the model assigns nonzero probability mass to an exponential number of $\it{noncanonical}$ token encodings of each character string -- these are token strings that decode to valid character strings but are impossible under the deterministic tokenizer (i.e., they will never be seen in any training corpus, no matter how large). This misallocation is both erroneous, as noncanonical strings never appear in training data, and wasteful, diverting probability mass away from plausible outputs. These are avoidable mistakes! In this work, we propose methods to enforce canonicality in token-level language models, ensuring that only canonical token strings are assigned positive probability. We present two approaches: (1) canonicality by conditioning, leveraging test-time inference strategies without additional training, and (2) canonicality by construction, a model parameterization that guarantees canonical outputs but requires training. We demonstrate that fixing canonicality mistakes improves the likelihood of held-out data for several models and corpora.

Syntactic and Semantic Control of Large Language Models via Sequential Monte Carlo

A wide range of LM applications require generating text that conforms to syntactic or semantic constraints. Imposing such constraints can be naturally framed as probabilistic conditioning, but exact generation from the resulting distribution -- which can differ substantially from the LM's base distribution -- is generally intractable. In this work, we develop an architecture for controlled LM generation based on sequential Monte Carlo (SMC). Our SMC framework allows us to flexibly incorporate domain- and problem-specific constraints at inference time, and efficiently reallocate computational resources in light of new information during the course of generation. By comparing to a number of alternatives and ablations on four challenging domains -- Python code generation for data science, text-to-SQL, goal inference, and molecule synthesis -- we demonstrate that, with little overhead, our approach allows small open-source language models to outperform models over 8x larger, as well as closed-source, fine-tuned ones. In support of the probabilistic perspective, we show that these performance improvements are driven by better approximation to the posterior distribution. Our system builds on the framework of Lew et al. (2023) and integrates with its language model probabilistic programming language, giving users a simple, programmable way to apply SMC to a broad variety of controlled generation problems.

An $\mathbf{L^*}$ Algorithm for Deterministic Weighted Regular Languages

Extracting finite state automata (FSAs) from black-box models offers a powerful approach to gaining interpretable insights into complex model behaviors. To support this pursuit, we present a weighted variant of Angluin's (1987) $\mathbf{L^*}$ algorithm for learning FSAs. We stay faithful to the original algorithm, devising a way to exactly learn deterministic weighted FSAs whose weights support division. Furthermore, we formulate the learning process in a manner that highlights the connection with FSA minimization, showing how $\mathbf{L^*}$ directly learns a minimal automaton for the target language.

On the Intersection of Context-Free and Regular Languages

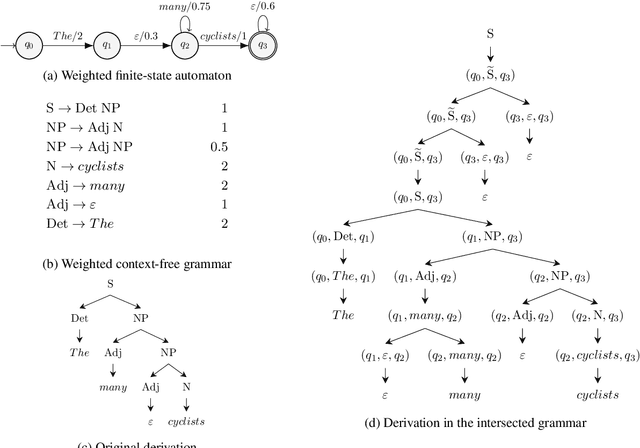
The Bar-Hillel construction is a classic result in formal language theory. It shows, by construction, that the intersection between a context-free language and a regular language is itself context-free. However, neither its original formulation (Bar-Hillel et al., 1961) nor its weighted extension (Nederhof and Satta, 2003) can handle automata with $\epsilon$-arcs. In this short note, we generalize the Bar-Hillel construction to correctly compute the intersection even when the automaton contains $\epsilon$-arcs. We further prove that our generalized construction leads to a grammar that encodes the structure of both the input automaton and grammar while retaining the asymptotic size of the original construction.