AnTKV: Anchor Token-Aware Sub-Bit Vector Quantization for KV Cache in Large Language Models

Quantization has emerged as an effective and lightweight solution to reduce the memory footprint of the KV cache in Large Language Models (LLMs). Nevertheless, minimizing the performance degradation caused by ultra-low-bit KV cache quantization remains a significant challenge. We observe that quantizing the KV cache of different tokens has varying impacts on the quality of attention outputs. To systematically investigate this phenomenon, we perform forward error propagation analysis on attention and propose the Anchor Score (AnS) that quantifies the sensitivity of each token's KV cache to quantization-induced error. Our analysis reveals significant disparities in AnS across tokens, suggesting that preserving a small subset with full precision (FP16) of high-AnS tokens can greatly mitigate accuracy loss in aggressive quantization scenarios. Based on this insight, we introduce AnTKV, a novel framework that leverages Anchor Token-aware Vector Quantization to compress the KV cache. Furthermore, to support efficient deployment, we design and develop a triton kernel that is fully compatible with FlashAttention, enabling fast online Anchor Token selection. AnTKV enables LLaMA-3-8B to handle context lengths up to 840K tokens on a single 80GB A100 GPU, while achieving up to 3.5x higher decoding throughput compared to the FP16 baseline. Our experiment results demonstrate that AnTKV matches or outperforms prior works such as KIVI, SKVQ, KVQuant, and CQ under 4-bit settings. More importantly, AnTKV achieves significantly lower perplexity under ultra-low-bit quantization on Mistral-7B, with only 6.32 at 1-bit and 8.87 at 0.375-bit, compared to the FP16 baseline of 4.73.

A rank-adaptive higher-order orthogonal iteration algorithm for truncated Tucker decomposition

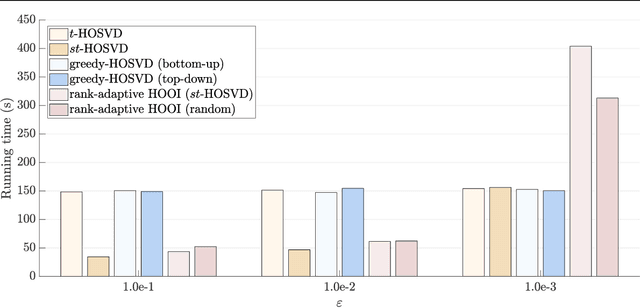
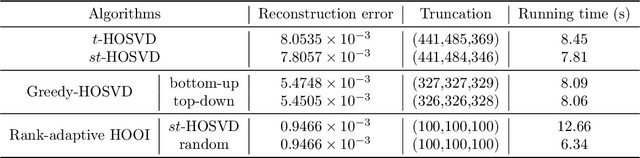
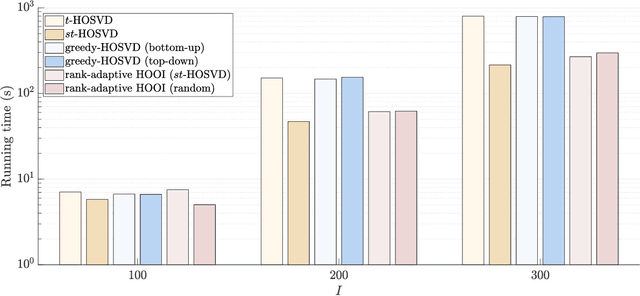
We propose a novel rank-adaptive higher-order orthogonal iteration (HOOI) algorithm to compute the truncated Tucker decomposition of higher-order tensors with a given error tolerance, and prove that the method is locally optimal and monotonically convergent. A series of numerical experiments related to both synthetic and real-world tensors are carried out to show that the proposed rank-adaptive HOOI algorithm is advantageous in terms of both accuracy and efficiency. Some further analysis on the HOOI algorithm and the classical alternating least squares method are presented to further understand why rank adaptivity can be introduced into the HOOI algorithm and how it works.

a-Tucker: Input-Adaptive and Matricization-Free Tucker Decomposition for Dense Tensors on CPUs and GPUs

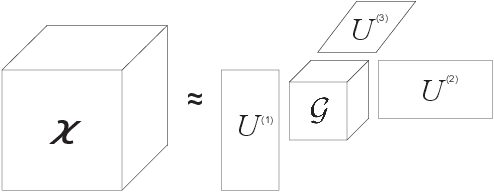
Tucker decomposition is one of the most popular models for analyzing and compressing large-scale tensorial data. Existing Tucker decomposition algorithms usually rely on a single solver to compute the factor matrices and core tensor, and are not flexible enough to adapt with the diversities of the input data and the hardware. Moreover, to exploit highly efficient GEMM kernels, most Tucker decomposition implementations make use of explicit matricizations, which could introduce extra costs in terms of data conversion and memory usage. In this paper, we present a-Tucker, a new framework for input-adaptive and matricization-free Tucker decomposition of dense tensors. A mode-wise flexible Tucker decomposition algorithm is proposed to enable the switch of different solvers for the factor matrices and core tensor, and a machine-learning adaptive solver selector is applied to automatically cope with the variations of both the input data and the hardware. To further improve the performance and enhance the memory efficiency, we implement a-Tucker in a fully matricization-free manner without any conversion between tensors and matrices. Experiments with a variety of synthetic and real-world tensors show that a-Tucker can substantially outperform existing works on both CPUs and GPUs.

Efficient Alternating Least Squares Algorithms for Truncated HOSVD of Higher-Order Tensors

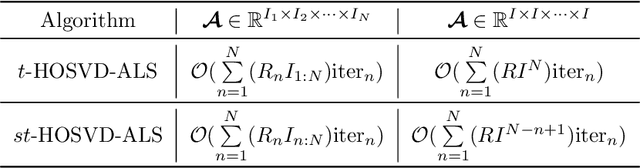
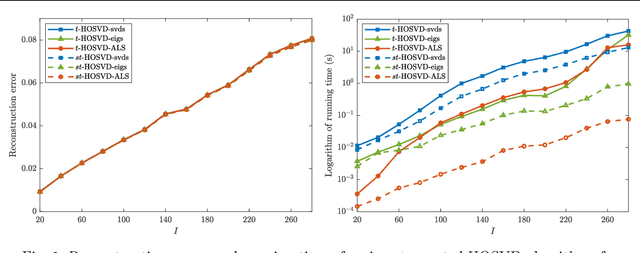
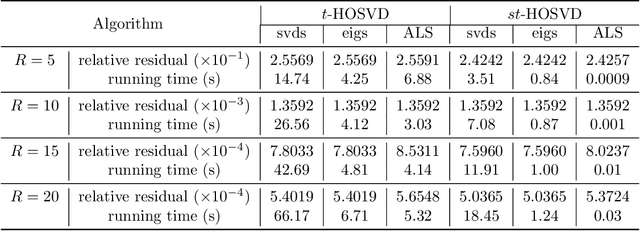
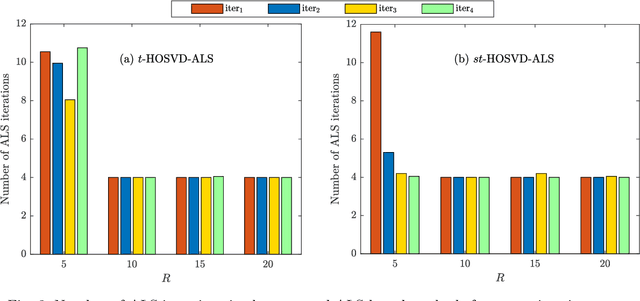
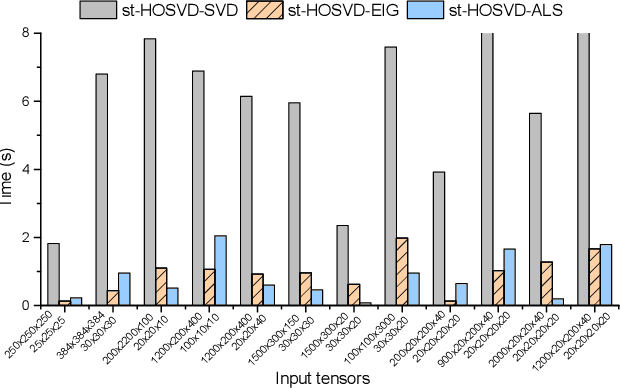
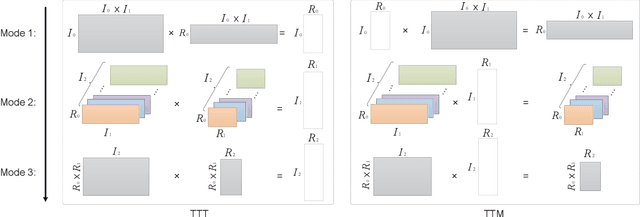
The truncated Tucker decomposition, also known as the truncated higher-order singular value decomposition (HOSVD), has been extensively utilized as an efficient tool in many applications. Popular direct methods for truncated HOSVD often suffer from the notorious intermediate data explosion issue and are not easy to parallelize. In this paper, we propose a class of new truncated HOSVD algorithms based on alternating least squares (ALS). The proposed ALS-based approaches are able to eliminate the redundant computations of the singular vectors of intermediate matrices and are therefore free of data explosion. Also, the new methods are more flexible with adjustable convergence tolerance and are intrinsically parallelizable on high-performance computers. Theoretical analysis reveals that the ALS iteration in the proposed algorithms is q-linear convergent with a relatively wide convergence region. Numerical experiments with both synthetic and real-world tensor data demonstrate that ALS-based methods can substantially reduce the total cost of the original ones and are highly scalable for parallel computing.