Partial Domain Adaptation via Importance Sampling-based Shift Correction

Partial domain adaptation (PDA) is a challenging task in real-world machine learning scenarios. It aims to transfer knowledge from a labeled source domain to a related unlabeled target domain, where the support set of the source label distribution subsumes the target one. Previous PDA works managed to correct the label distribution shift by weighting samples in the source domain. However, the simple reweighing technique cannot explore the latent structure and sufficiently use the labeled data, and then models are prone to over-fitting on the source domain. In this work, we propose a novel importance sampling-based shift correction (IS$^2$C) method, where new labeled data are sampled from a built sampling domain, whose label distribution is supposed to be the same as the target domain, to characterize the latent structure and enhance the generalization ability of the model. We provide theoretical guarantees for IS$^2$C by proving that the generalization error can be sufficiently dominated by IS$^2$C. In particular, by implementing sampling with the mixture distribution, the extent of shift between source and sampling domains can be connected to generalization error, which provides an interpretable way to build IS$^2$C. To improve knowledge transfer, an optimal transport-based independence criterion is proposed for conditional distribution alignment, where the computation of the criterion can be adjusted to reduce the complexity from $\mathcal{O}(n^3)$ to $\mathcal{O}(n^2)$ in realistic PDA scenarios. Extensive experiments on PDA benchmarks validate the theoretical results and demonstrate the effectiveness of our IS$^2$C over existing methods.

Bures Joint Distribution Alignment with Dynamic Margin for Unsupervised Domain Adaptation

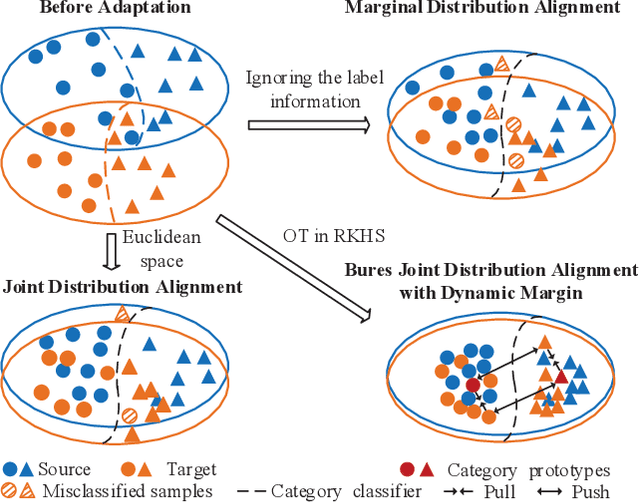
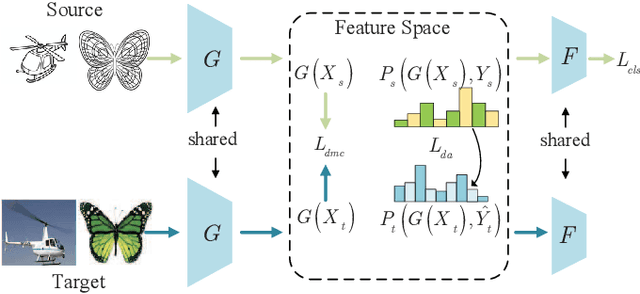
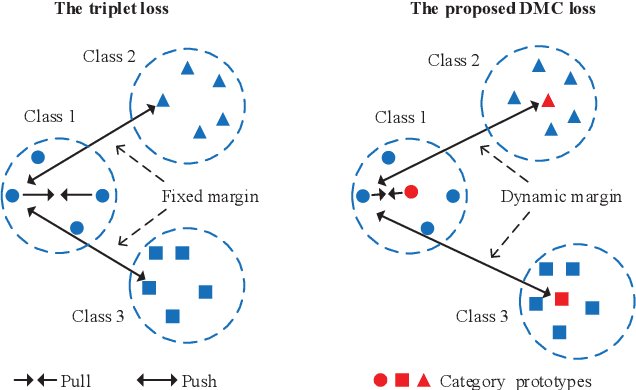
Unsupervised domain adaptation (UDA) is one of the prominent tasks of transfer learning, and it provides an effective approach to mitigate the distribution shift between the labeled source domain and the unlabeled target domain. Prior works mainly focus on aligning the marginal distributions or the estimated class-conditional distributions. However, the joint dependency among the feature and the label is crucial for the adaptation task and is not fully exploited. To address this problem, we propose the Bures Joint Distribution Alignment (BJDA) algorithm which directly models the joint distribution shift based on the optimal transport theory in the infinite-dimensional kernel spaces. Specifically, we propose a novel alignment loss term that minimizes the kernel Bures-Wasserstein distance between the joint distributions. Technically, BJDA can effectively capture the nonlinear structures underlying the data. In addition, we introduce a dynamic margin in contrastive learning phase to flexibly characterize the class separability and improve the discriminative ability of representations. It also avoids the cross-validation procedure to determine the margin parameter in traditional triplet loss based methods. Extensive experiments show that BJDA is very effective for the UDA tasks, as it outperforms state-of-the-art algorithms in most experimental settings. In particular, BJDA improves the average accuracy of UDA tasks by 2.8% on Adaptiope, 1.4% on Office-Caltech10, and 1.1% on ImageCLEF-DA.

Discriminative Residual Analysis for Image Set Classification with Posture and Age Variations

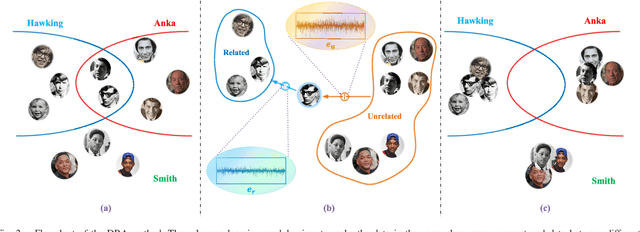
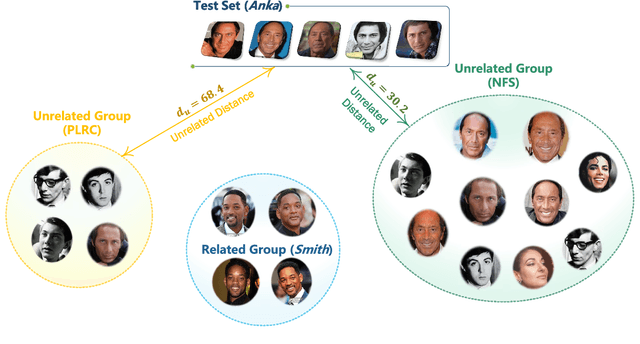
Image set recognition has been widely applied in many practical problems like real-time video retrieval and image caption tasks. Due to its superior performance, it has grown into a significant topic in recent years. However, images with complicated variations, e.g., postures and human ages, are difficult to address, as these variations are continuous and gradual with respect to image appearance. Consequently, the crucial point of image set recognition is to mine the intrinsic connection or structural information from the image batches with variations. In this work, a Discriminant Residual Analysis (DRA) method is proposed to improve the classification performance by discovering discriminant features in related and unrelated groups. Specifically, DRA attempts to obtain a powerful projection which casts the residual representations into a discriminant subspace. Such a projection subspace is expected to magnify the useful information of the input space as much as possible, then the relation between the training set and the test set described by the given metric or distance will be more precise in the discriminant subspace. We also propose a nonfeasance strategy by defining another approach to construct the unrelated groups, which help to reduce furthermore the cost of sampling errors. Two regularization approaches are used to deal with the probable small sample size problem. Extensive experiments are conducted on benchmark databases, and the results show superiority and efficiency of the new methods.