Soft-Masked Semi-Dual Optimal Transport for Partial Domain Adaptation

Visual domain adaptation aims to learn discriminative and domain-invariant representation for an unlabeled target domain by leveraging knowledge from a labeled source domain. Partial domain adaptation (PDA) is a general and practical scenario in which the target label space is a subset of the source one. The challenges of PDA exist due to not only domain shift but also the non-identical label spaces of domains. In this paper, a Soft-masked Semi-dual Optimal Transport (SSOT) method is proposed to deal with the PDA problem. Specifically, the class weights of domains are estimated, and then a reweighed source domain is constructed, which is favorable in conducting class-conditional distribution matching with the target domain. A soft-masked transport distance matrix is constructed by category predictions, which will enhance the class-oriented representation ability of optimal transport in the shared feature space. To deal with large-scale optimal transport problems, the semi-dual formulation of the entropy-regularized Kantorovich problem is employed since it can be optimized by gradient-based algorithms. Further, a neural network is exploited to approximate the Kantorovich potential due to its strong fitting ability. This network parametrization also allows the generalization of the dual variable outside the supports of the input distribution. The SSOT model is built upon neural networks, which can be optimized alternately in an end-to-end manner. Extensive experiments are conducted on four benchmark datasets to demonstrate the effectiveness of SSOT.

Maximizing Conditional Independence for Unsupervised Domain Adaptation

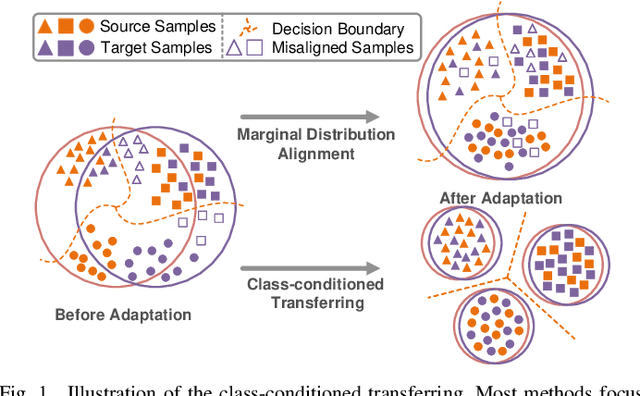
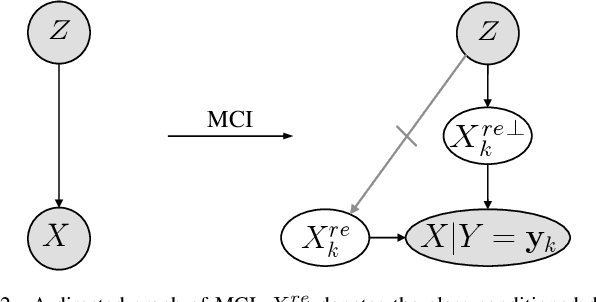
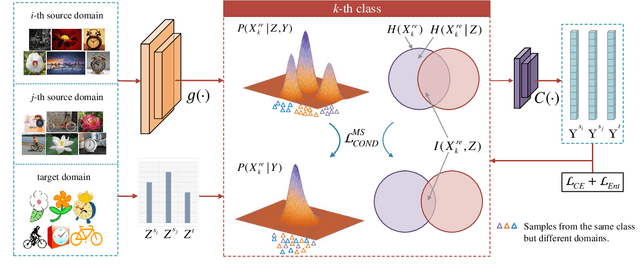
Unsupervised domain adaptation studies how to transfer a learner from a labeled source domain to an unlabeled target domain with different distributions. Existing methods mainly focus on matching the marginal distributions of the source and target domains, which probably lead a misalignment of samples from the same class but different domains. In this paper, we deal with this misalignment by achieving the class-conditioned transferring from a new perspective. We aim to maximize the conditional independence of feature and domain given class in the reproducing kernel Hilbert space. The optimization of the conditional independence measure can be viewed as minimizing a surrogate of a certain mutual information between feature and domain. An interpretable empirical estimation of the conditional dependence is deduced and connected with the unconditional case. Besides, we provide an upper bound on the target error by taking the class-conditional distribution into account, which provides a new theoretical insight for most class-conditioned transferring methods. In addition to unsupervised domain adaptation, we extend our method to the multi-source scenario in a natural and elegant way. Extensive experiments on four benchmarks validate the effectiveness of the proposed models in both unsupervised domain adaptation and multiple source domain adaptation.