Fourier Sparse Leverage Scores and Approximate Kernel Learning

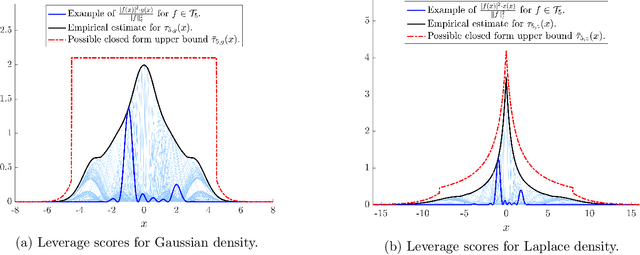
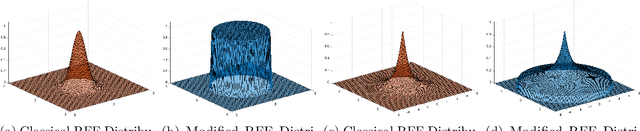
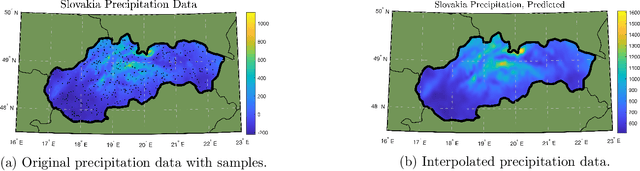
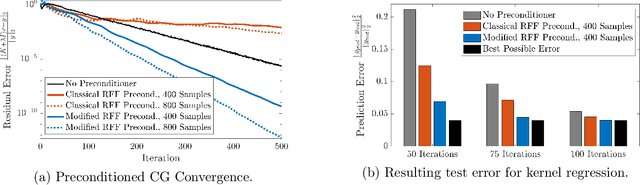
We prove new explicit upper bounds on the leverage scores of Fourier sparse functions under both the Gaussian and Laplace measures. In particular, we study $s$-sparse functions of the form $f(x) = \sum_{j=1}^s a_j e^{i \lambda_j x}$ for coefficients $a_j \in \mathbb{C}$ and frequencies $\lambda_j \in \mathbb{R}$. Bounding Fourier sparse leverage scores under various measures is of pure mathematical interest in approximation theory, and our work extends existing results for the uniform measure [Erd17,CP19a]. Practically, our bounds are motivated by two important applications in machine learning: 1. Kernel Approximation. They yield a new random Fourier features algorithm for approximating Gaussian and Cauchy (rational quadratic) kernel matrices. For low-dimensional data, our method uses a near optimal number of features, and its runtime is polynomial in the $statistical\ dimension$ of the approximated kernel matrix. It is the first "oblivious sketching method" with this property for any kernel besides the polynomial kernel, resolving an open question of [AKM+17,AKK+20b]. 2. Active Learning. They can be used as non-uniform sampling distributions for robust active learning when data follows a Gaussian or Laplace distribution. Using the framework of [AKM+19], we provide essentially optimal results for bandlimited and multiband interpolation, and Gaussian process regression. These results generalize existing work that only applies to uniformly distributed data.

Projection-Cost-Preserving Sketches: Proof Strategies and Constructions

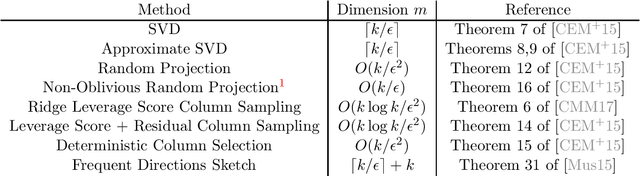
In this note we illustrate how common matrix approximation methods, such as random projection and random sampling, yield projection-cost-preserving sketches, as introduced in [FSS13, CEM+15]. A projection-cost-preserving sketch is a matrix approximation which, for a given parameter $k$, approximately preserves the distance of the target matrix to all $k$-dimensional subspaces. Such sketches have applications to scalable algorithms for linear algebra, data science, and machine learning. Our goal is to simplify the presentation of proof techniques introduced in [CEM+15] and [CMM17] so that they can serve as a guide for future work. We also refer the reader to [CYD19], which gives a similar simplified exposition of the proof covered in Section 2.

Sample Efficient Toeplitz Covariance Estimation

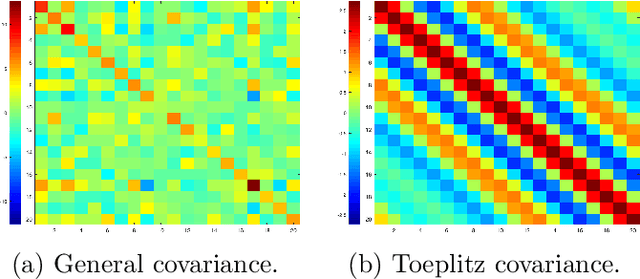
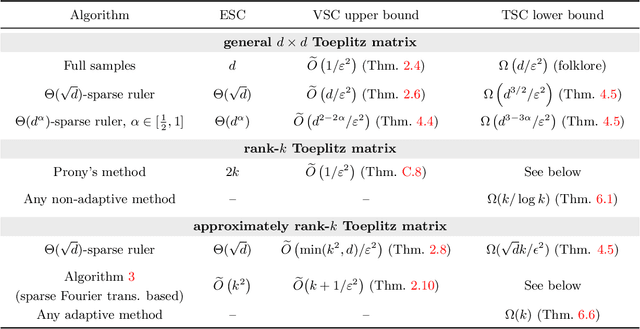
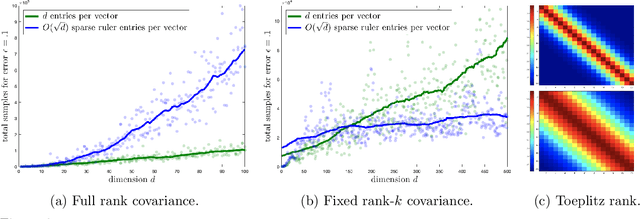
We study the sample complexity of estimating the covariance matrix $T$ of a distribution $\mathcal{D}$ over $d$-dimensional vectors, under the assumption that $T$ is Toeplitz. This assumption arises in many signal processing problems, where the covariance between any two measurements only depends on the time or distance between those measurements. We are interested in estimation strategies that may choose to view only a subset of entries in each vector sample $x \sim \mathcal{D}$, which often equates to reducing hardware and communication requirements in applications ranging from wireless signal processing to advanced imaging. Our goal is to minimize both 1) the number of vector samples drawn from $\mathcal{D}$ and 2) the number of entries accessed in each sample. We provide some of the first non-asymptotic bounds on these sample complexity measures that exploit $T$'s Toeplitz structure, and by doing so, significantly improve on results for generic covariance matrices. Our bounds follow from a novel analysis of classical and widely used estimation algorithms (along with some new variants), including methods based on selecting entries from each vector sample according to a so-called sparse ruler. In many cases, we pair our upper bounds with matching or nearly matching lower bounds. In addition to results that hold for any Toeplitz $T$, we further study the important setting when $T$ is close to low-rank, which is often the case in practice. We show that methods based on sparse rulers perform even better in this setting, with sample complexity scaling sublinearly in $d$. Motivated by this finding, we develop a new covariance estimation strategy that further improves on all existing methods in the low-rank case: when $T$ is rank-$k$ or nearly rank-$k$, it achieves sample complexity depending polynomially on $k$ and only logarithmically on $d$.

Low-Rank Approximation from Communication Complexity

In low-rank approximation with missing entries, given $A\in \mathbb{R}^{n\times n}$ and binary $W \in \{0,1\}^{n\times n}$, the goal is to find a rank-$k$ matrix $L$ for which: $$cost(L)=\sum_{i=1}^{n} \sum_{j=1}^{n}W_{i,j}\cdot (A_{i,j} - L_{i,j})^2\le OPT+\epsilon \|A\|_F^2,$$ where $OPT=\min_{rank-k\ \hat{L}}cost(\hat L)$. This problem is also known as matrix completion and, depending on the choice of $W$, captures low-rank plus diagonal decomposition, robust PCA, low-rank recovery from monotone missing data, and a number of other important problems. Many of these problems are NP-hard, and while algorithms with provable guarantees are known in some cases, they either 1) run in time $n^{\Omega(k^2/\epsilon)}$, or 2) make strong assumptions, e.g., that $A$ is incoherent or that $W$ is random. In this work, we consider $bicriteria\ algorithms$, which output $L$ with rank $k' > k$. We prove that a common heuristic, which simply sets $A$ to $0$ where $W$ is $0$, and then computes a standard low-rank approximation, achieves the above approximation bound with rank $k'$ depending on the $communication\ complexity$ of $W$. Namely, interpreting $W$ as the communication matrix of a Boolean function $f(x,y)$ with $x,y\in \{0,1\}^{\log n}$, it suffices to set $k'=O(k\cdot 2^{R^{1-sided}_{\epsilon}(f)})$, where $R^{1-sided}_{\epsilon}(f)$ is the randomized communication complexity of $f$ with $1$-sided error probability $\epsilon$. For many problems, this yields bicriteria algorithms with $k'=k\cdot poly((\log n)/\epsilon)$. We prove a similar bound using the randomized communication complexity with $2$-sided error. Further, we show that different models of communication yield algorithms for natural variants of the problem. E.g., multi-player communication complexity connects to tensor decomposition and non-deterministic communication complexity to Boolean low-rank factorization.

A Universal Sampling Method for Reconstructing Signals with Simple Fourier Transforms

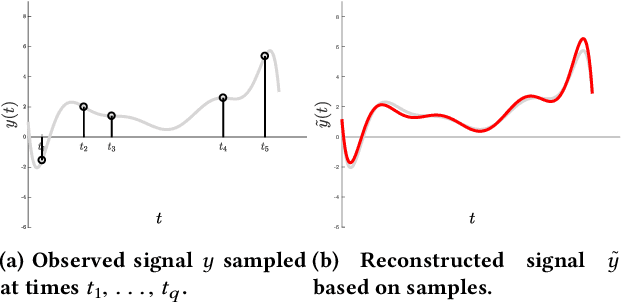
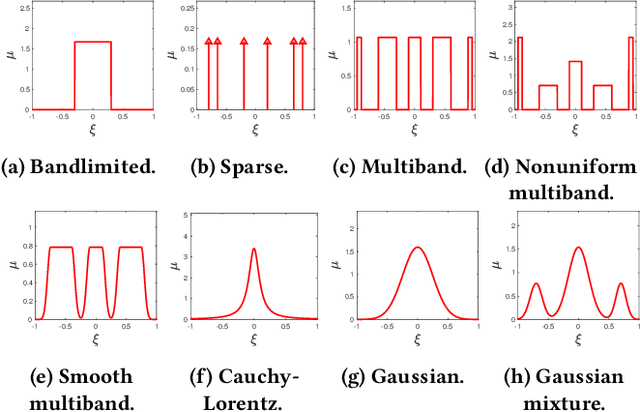
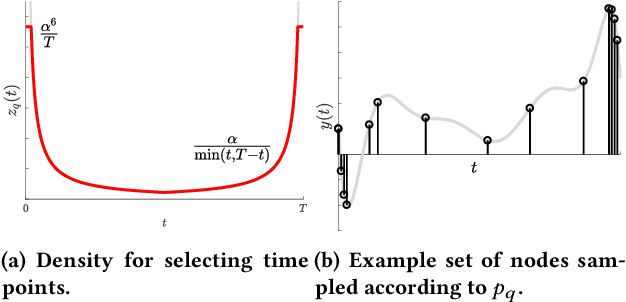
Reconstructing continuous signals from a small number of discrete samples is a fundamental problem across science and engineering. In practice, we are often interested in signals with 'simple' Fourier structure, such as bandlimited, multiband, and Fourier sparse signals. More broadly, any prior knowledge about a signal's Fourier power spectrum can constrain its complexity. Intuitively, signals with more highly constrained Fourier structure require fewer samples to reconstruct. We formalize this intuition by showing that, roughly, a continuous signal from a given class can be approximately reconstructed using a number of samples proportional to the *statistical dimension* of the allowed power spectrum of that class. Further, in nearly all settings, this natural measure tightly characterizes the sample complexity of signal reconstruction. Surprisingly, we also show that, up to logarithmic factors, a universal non-uniform sampling strategy can achieve this optimal complexity for *any class of signals*. We present a simple and efficient algorithm for recovering a signal from the samples taken. For bandlimited and sparse signals, our method matches the state-of-the-art. At the same time, it gives the first computationally and sample efficient solution to a broad range of problems, including multiband signal reconstruction and kriging and Gaussian process regression tasks in one dimension. Our work is based on a novel connection between randomized linear algebra and signal reconstruction with constrained Fourier structure. We extend tools based on statistical leverage score sampling and column-based matrix reconstruction to the approximation of continuous linear operators that arise in signal reconstruction. We believe that these extensions are of independent interest and serve as a foundation for tackling a broad range of continuous time problems using randomized methods.

Random Fourier Features for Kernel Ridge Regression: Approximation Bounds and Statistical Guarantees

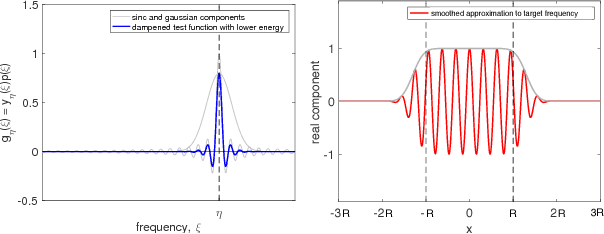
Random Fourier features is one of the most popular techniques for scaling up kernel methods, such as kernel ridge regression. However, despite impressive empirical results, the statistical properties of random Fourier features are still not well understood. In this paper we take steps toward filling this gap. Specifically, we approach random Fourier features from a spectral matrix approximation point of view, give tight bounds on the number of Fourier features required to achieve a spectral approximation, and show how spectral matrix approximation bounds imply statistical guarantees for kernel ridge regression. Qualitatively, our results are twofold: on the one hand, we show that random Fourier feature approximation can provably speed up kernel ridge regression under reasonable assumptions. At the same time, we show that the method is suboptimal, and sampling from a modified distribution in Fourier space, given by the leverage function of the kernel, yields provably better performance. We study this optimal sampling distribution for the Gaussian kernel, achieving a nearly complete characterization for the case of low-dimensional bounded datasets. Based on this characterization, we propose an efficient sampling scheme with guarantees superior to random Fourier features in this regime.

Learning Networks from Random Walk-Based Node Similarities

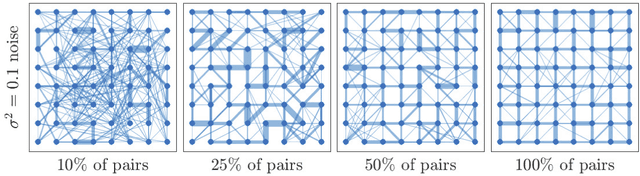
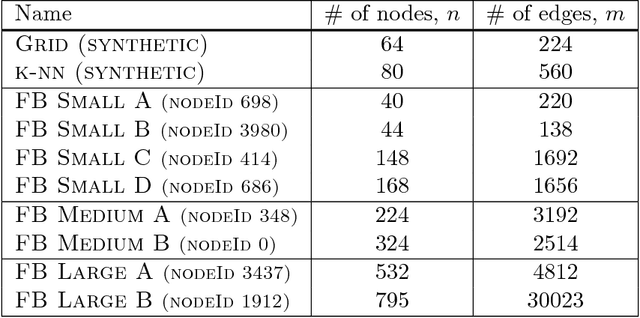
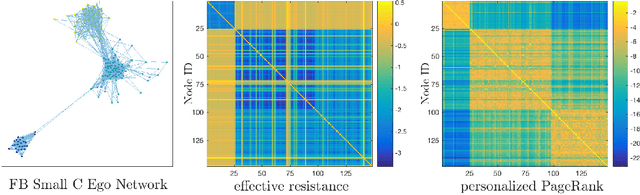
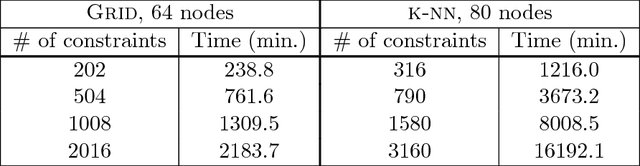
Digital presence in the world of online social media entails significant privacy risks. In this work we consider a privacy threat to a social network in which an attacker has access to a subset of random walk-based node similarities, such as effective resistances (i.e., commute times) or personalized PageRank scores. Using these similarities, the attacker's goal is to infer as much information as possible about the underlying network, including any remaining unknown pairwise node similarities and edges. For the effective resistance metric, we show that with just a small subset of measurements, the attacker can learn a large fraction of edges in a social network, even when the measurements are noisy. We also show that it is possible to learn a graph which accurately matches the underlying network on all other effective resistances. This second observation is interesting from a data mining perspective, since it can be expensive to accurately compute all effective resistances. As an alternative, our graphs learned from just a subset of approximate effective resistances can be used as surrogates in a wide range of applications that use effective resistances to probe graph structure, including for graph clustering, node centrality evaluation, and anomaly detection. We obtain our results by formalizing the graph learning objective mathematically, using two optimization problems. One formulation is convex and can be solved provably in polynomial time. The other is not, but we solve it efficiently with projected gradient and coordinate descent. We demonstrate the effectiveness of these methods on a number of social networks obtained from Facebook. We also discuss how our methods can be generalized to other random walk-based similarities, such as personalized PageRank. Our code is available at https://github.com/cnmusco/graph-similarity-learning.

Minimizing Polarization and Disagreement in Social Networks

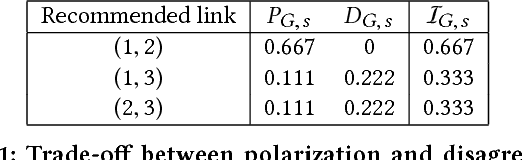
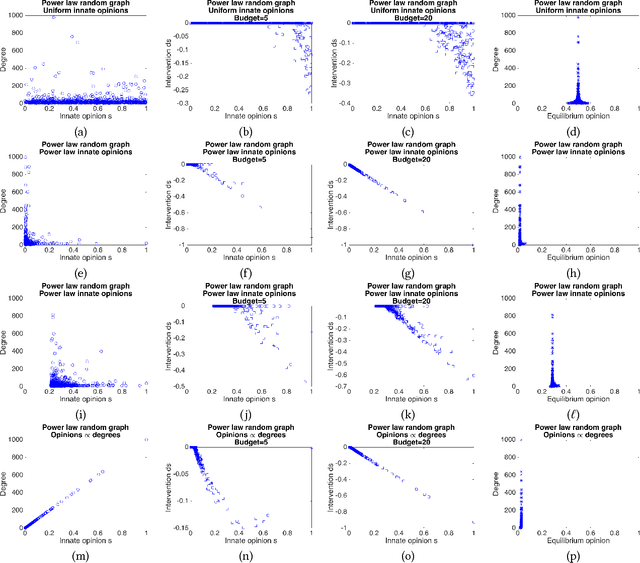
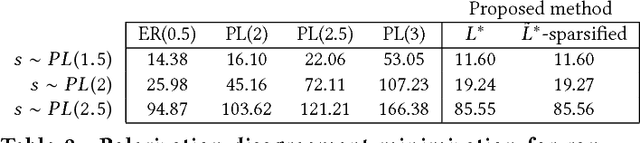
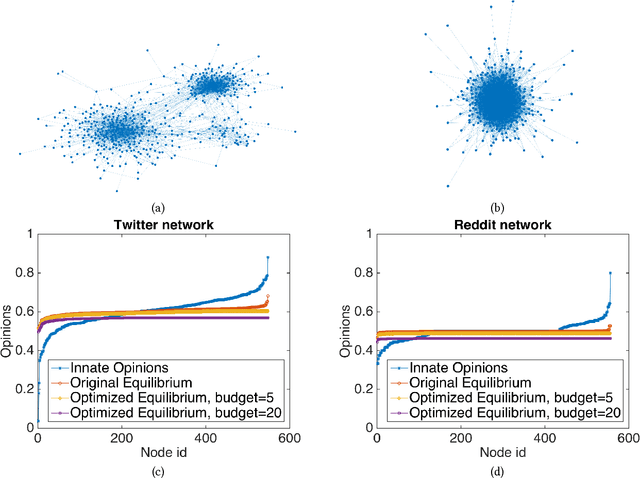
The rise of social media and online social networks has been a disruptive force in society. Opinions are increasingly shaped by interactions on online social media, and social phenomena including disagreement and polarization are now tightly woven into everyday life. In this work we initiate the study of the following question: given $n$ agents, each with its own initial opinion that reflects its core value on a topic, and an opinion dynamics model, what is the structure of a social network that minimizes {\em polarization} and {\em disagreement} simultaneously? This question is central to recommender systems: should a recommender system prefer a link suggestion between two online users with similar mindsets in order to keep disagreement low, or between two users with different opinions in order to expose each to the other's viewpoint of the world, and decrease overall levels of polarization? Our contributions include a mathematical formalization of this question as an optimization problem and an exact, time-efficient algorithm. We also prove that there always exists a network with $O(n/\epsilon^2)$ edges that is a $(1+\epsilon)$ approximation to the optimum. For a fixed graph, we additionally show how to optimize our objective function over the agents' innate opinions in polynomial time. We perform an empirical study of our proposed methods on synthetic and real-world data that verify their value as mining tools to better understand the trade-off between of disagreement and polarization. We find that there is a lot of space to reduce both polarization and disagreement in real-world networks; for instance, on a Reddit network where users exchange comments on politics, our methods achieve a $\sim 60\,000$-fold reduction in polarization and disagreement.

Recursive Sampling for the Nyström Method

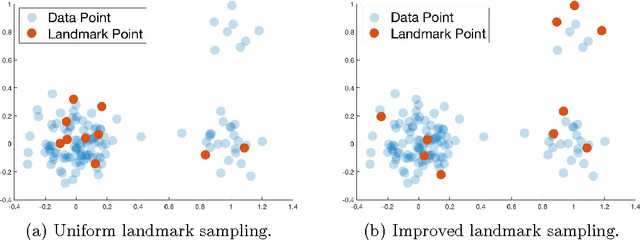
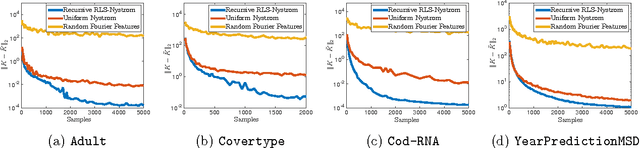
We give the first algorithm for kernel Nystr\"om approximation that runs in *linear time in the number of training points* and is provably accurate for all kernel matrices, without dependence on regularity or incoherence conditions. The algorithm projects the kernel onto a set of $s$ landmark points sampled by their *ridge leverage scores*, requiring just $O(ns)$ kernel evaluations and $O(ns^2)$ additional runtime. While leverage score sampling has long been known to give strong theoretical guarantees for Nystr\"om approximation, by employing a fast recursive sampling scheme, our algorithm is the first to make the approach scalable. Empirically we show that it finds more accurate, lower rank kernel approximations in less time than popular techniques such as uniformly sampled Nystr\"om approximation and the random Fourier features method.

Input Sparsity Time Low-Rank Approximation via Ridge Leverage Score Sampling

We present a new algorithm for finding a near optimal low-rank approximation of a matrix $A$ in $O(nnz(A))$ time. Our method is based on a recursive sampling scheme for computing a representative subset of $A$'s columns, which is then used to find a low-rank approximation. This approach differs substantially from prior $O(nnz(A))$ time algorithms, which are all based on fast Johnson-Lindenstrauss random projections. It matches the guarantees of these methods while offering a number of advantages. Not only are sampling algorithms faster for sparse and structured data, but they can also be applied in settings where random projections cannot. For example, we give new single-pass streaming algorithms for the column subset selection and projection-cost preserving sample problems. Our method has also been used to give the fastest algorithms for provably approximating kernel matrices [MM16].