On the convergence of the Metropolis algorithm with fixed-order updates for multivariate binary probability distributions

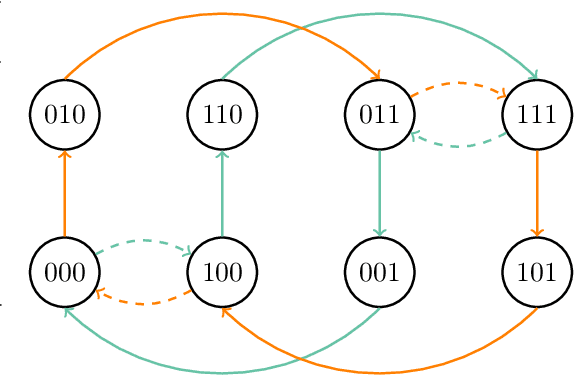
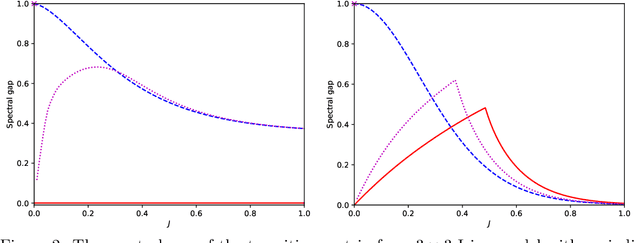
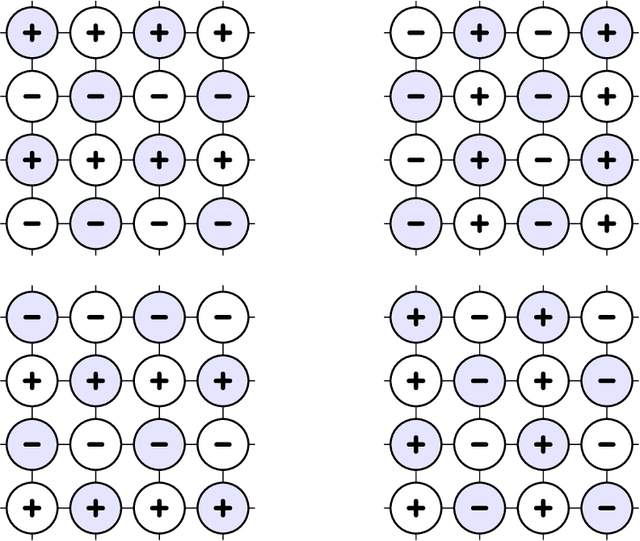
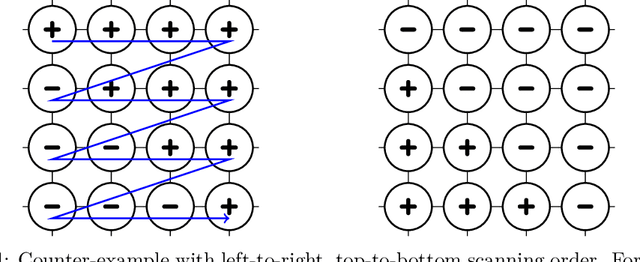
The Metropolis algorithm is arguably the most fundamental Markov chain Monte Carlo (MCMC) method. But the algorithm is not guaranteed to converge to the desired distribution in the case of multivariate binary distributions (e.g., Ising models or stochastic neural networks such as Boltzmann machines) if the variables (sites or neurons) are updated in a fixed order, a setting commonly used in practice. The reason is that the corresponding Markov chain may not be irreducible. We propose a modified Metropolis transition operator that behaves almost always identically to the standard Metropolis operator and prove that it ensures irreducibility and convergence to the limiting distribution in the multivariate binary case with fixed-order updates. The result provides an explanation for the behaviour of Metropolis MCMC in that setting and closes a long-standing theoretical gap. We experimentally studied the standard and modified Metropolis operator for models were they actually behave differently. If the standard algorithm also converges, the modified operator exhibits similar (if not better) performance in terms of convergence speed.

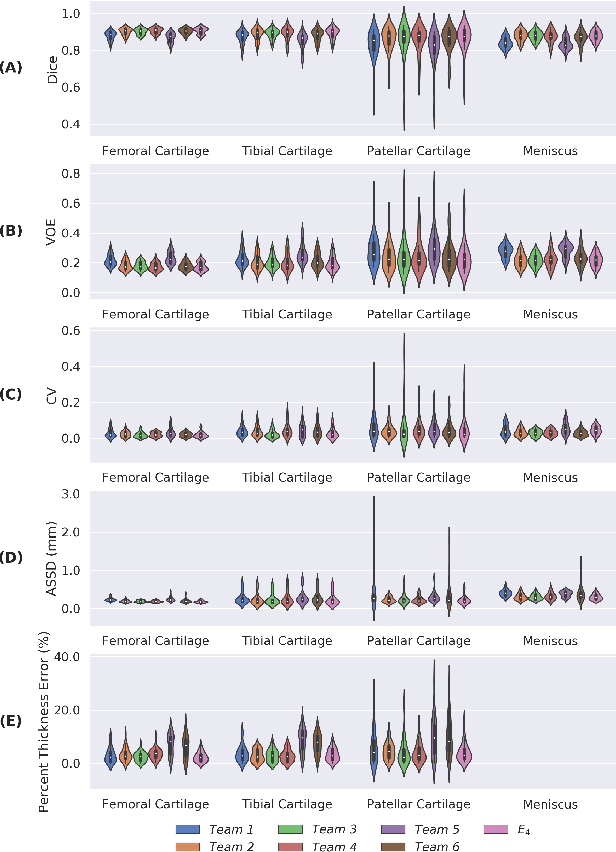
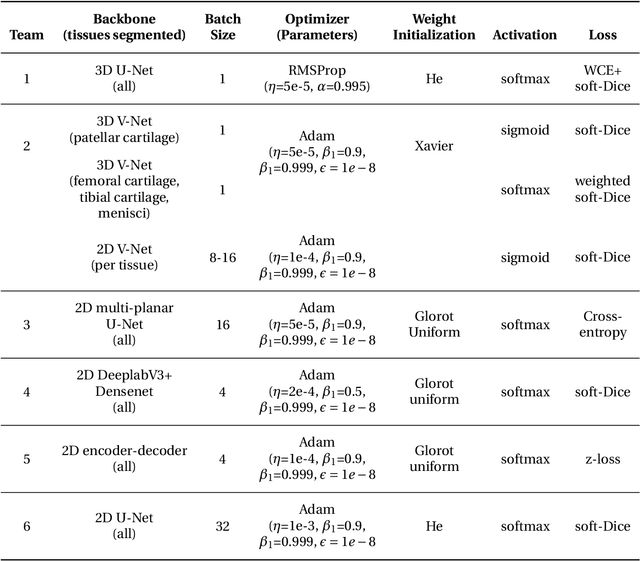
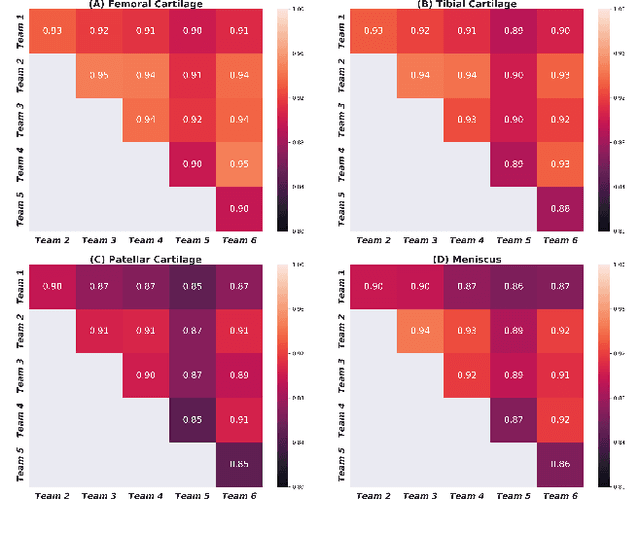
The International Workshop on Osteoarthritis Imaging Knee MRI Segmentation Challenge: A Multi-Institute Evaluation and Analysis Framework on a Standardized Dataset

Purpose: To organize a knee MRI segmentation challenge for characterizing the semantic and clinical efficacy of automatic segmentation methods relevant for monitoring osteoarthritis progression. Methods: A dataset partition consisting of 3D knee MRI from 88 subjects at two timepoints with ground-truth articular (femoral, tibial, patellar) cartilage and meniscus segmentations was standardized. Challenge submissions and a majority-vote ensemble were evaluated using Dice score, average symmetric surface distance, volumetric overlap error, and coefficient of variation on a hold-out test set. Similarities in network segmentations were evaluated using pairwise Dice correlations. Articular cartilage thickness was computed per-scan and longitudinally. Correlation between thickness error and segmentation metrics was measured using Pearson's coefficient. Two empirical upper bounds for ensemble performance were computed using combinations of model outputs that consolidated true positives and true negatives. Results: Six teams (T1-T6) submitted entries for the challenge. No significant differences were observed across all segmentation metrics for all tissues (p=1.0) among the four top-performing networks (T2, T3, T4, T6). Dice correlations between network pairs were high (>0.85). Per-scan thickness errors were negligible among T1-T4 (p=0.99) and longitudinal changes showed minimal bias (<0.03mm). Low correlations (<0.41) were observed between segmentation metrics and thickness error. The majority-vote ensemble was comparable to top performing networks (p=1.0). Empirical upper bound performances were similar for both combinations (p=1.0). Conclusion: Diverse networks learned to segment the knee similarly where high segmentation accuracy did not correlate to cartilage thickness accuracy. Voting ensembles did not outperform individual networks but may help regularize individual models.

Label-similarity Curriculum Learning

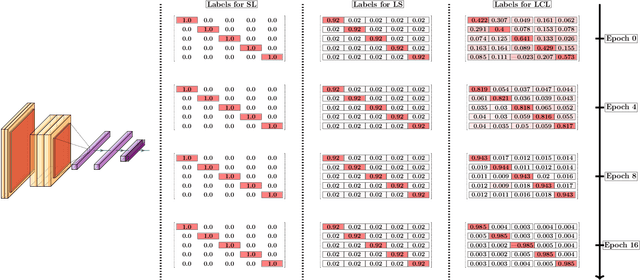
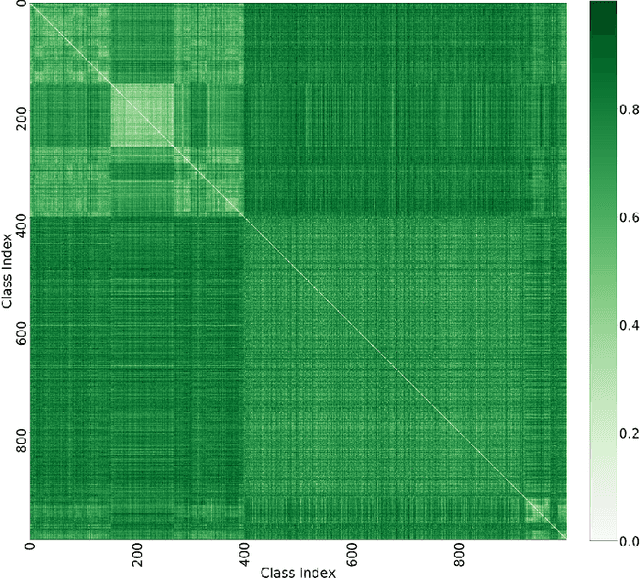
Curriculum learning can improve neural network training by guiding the optimization to desirable optima. We propose a novel curriculum learning approach for image classification that adapts the loss function by changing the label representation. The idea is to use a probability distribution over classes as target label, where the class probabilities reflect the similarity to the true class. Gradually, this label representation is shifted towards the standard one-hot-encoding. That is, in the beginning minor mistakes are corrected less than large mistakes, resembling a teaching process in which broad concepts are explained first before subtle differences are taught. The class similarity can be based on prior knowledge. For the special case of the labels being natural words, we propose a generic way to automatically compute the similarities. The natural words are embedded into Euclidean space using a standard word embedding. The probability of each class is then a function of the cosine similarity between the vector representations of the class and the true label. The proposed label-similarity curriculum learning (LCL) approach was empirically evaluated on several popular deep learning architectures for image classification task applied to three datasets, ImageNet, CIFAR100, and AWA2. In all scenarios, LCL was able to improve the classification accuracy on the test data compared to standard training.

One Network to Segment Them All: A General, Lightweight System for Accurate 3D Medical Image Segmentation

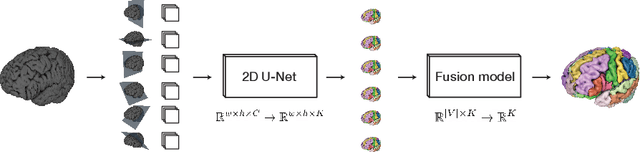
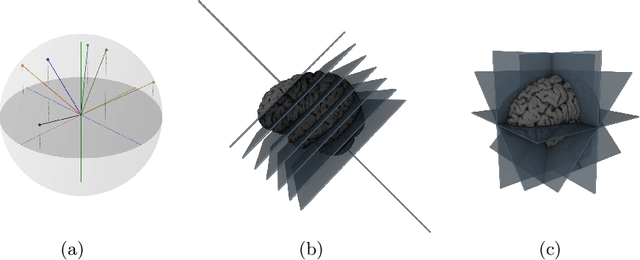
Many recent medical segmentation systems rely on powerful deep learning models to solve highly specific tasks. To maximize performance, it is standard practice to evaluate numerous pipelines with varying model topologies, optimization parameters, pre- & postprocessing steps, and even model cascades. It is often not clear how the resulting pipeline transfers to different tasks. We propose a simple and thoroughly evaluated deep learning framework for segmentation of arbitrary medical image volumes. The system requires no task-specific information, no human interaction and is based on a fixed model topology and a fixed hyperparameter set, eliminating the process of model selection and its inherent tendency to cause method-level over-fitting. The system is available in open source and does not require deep learning expertise to use. Without task-specific modifications, the system performed better than or similar to highly specialized deep learning methods across 3 separate segmentation tasks. In addition, it ranked 5-th and 6-th in the first and second round of the 2018 Medical Segmentation Decathlon comprising another 10 tasks. The system relies on multi-planar data augmentation which facilitates the application of a single 2D architecture based on the familiar U-Net. Multi-planar training combines the parameter efficiency of a 2D fully convolutional neural network with a systematic train- and test-time augmentation scheme, which allows the 2D model to learn a representation of the 3D image volume that fosters generalization.

U-Time: A Fully Convolutional Network for Time Series Segmentation Applied to Sleep Staging

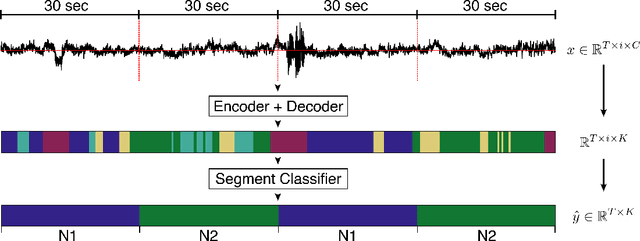
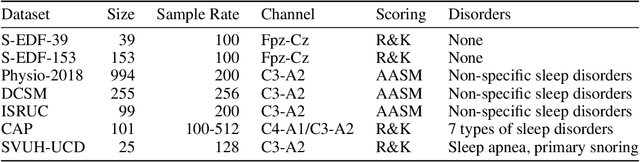
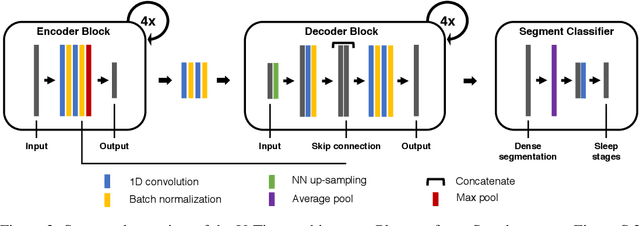
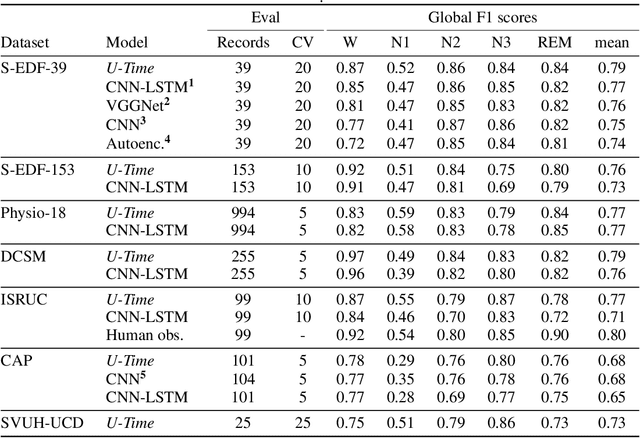
Neural networks are becoming more and more popular for the analysis of physiological time-series. The most successful deep learning systems in this domain combine convolutional and recurrent layers to extract useful features to model temporal relations. Unfortunately, these recurrent models are difficult to tune and optimize. In our experience, they often require task-specific modifications, which makes them challenging to use for non-experts. We propose U-Time, a fully feed-forward deep learning approach to physiological time series segmentation developed for the analysis of sleep data. U-Time is a temporal fully convolutional network based on the U-Net architecture that was originally proposed for image segmentation. U-Time maps sequential inputs of arbitrary length to sequences of class labels on a freely chosen temporal scale. This is done by implicitly classifying every individual time-point of the input signal and aggregating these classifications over fixed intervals to form the final predictions. We evaluated U-Time for sleep stage classification on a large collection of sleep electroencephalography (EEG) datasets. In all cases, we found that U-Time reaches or outperforms current state-of-the-art deep learning models while being much more robust in the training process and without requiring architecture or hyperparameter adaptation across tasks.

Knowledge distillation for semi-supervised domain adaptation

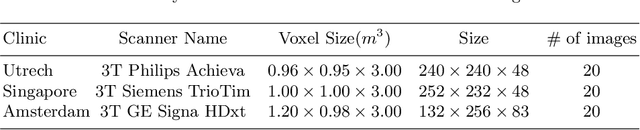
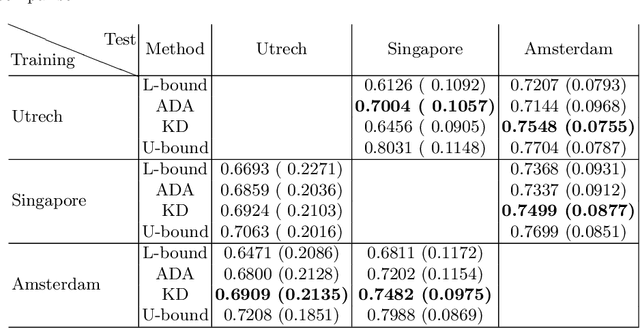
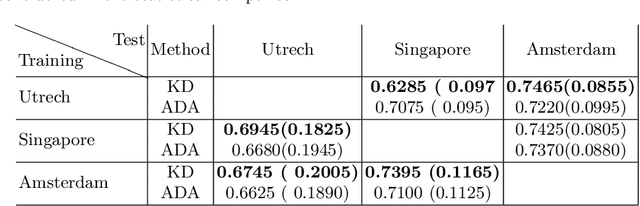
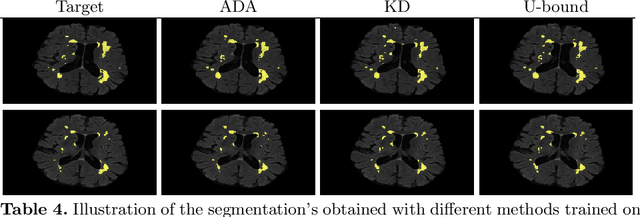
In the absence of sufficient data variation (e.g., scanner and protocol variability) in annotated data, deep neural networks (DNNs) tend to overfit during training. As a result, their performance is significantly lower on data from unseen sources compared to the performance on data from the same source as the training data. Semi-supervised domain adaptation methods can alleviate this problem by tuning networks to new target domains without the need for annotated data from these domains. Adversarial domain adaptation (ADA) methods are a popular choice that aim to train networks in such a way that the features generated are domain agnostic. However, these methods require careful dataset-specific selection of hyperparameters such as the complexity of the discriminator in order to achieve a reasonable performance. We propose to use knowledge distillation (KD) -- an efficient way of transferring knowledge between different DNNs -- for semi-supervised domain adaption of DNNs. It does not require dataset-specific hyperparameter tuning, making it generally applicable. The proposed method is compared to ADA for segmentation of white matter hyperintensities (WMH) in magnetic resonance imaging (MRI) scans generated by scanners that are not a part of the training set. Compared with both the baseline DNN (trained on source domain only and without any adaption to target domain) and with using ADA for semi-supervised domain adaptation, the proposed method achieves significantly higher WMH dice scores.

On PAC-Bayesian Bounds for Random Forests

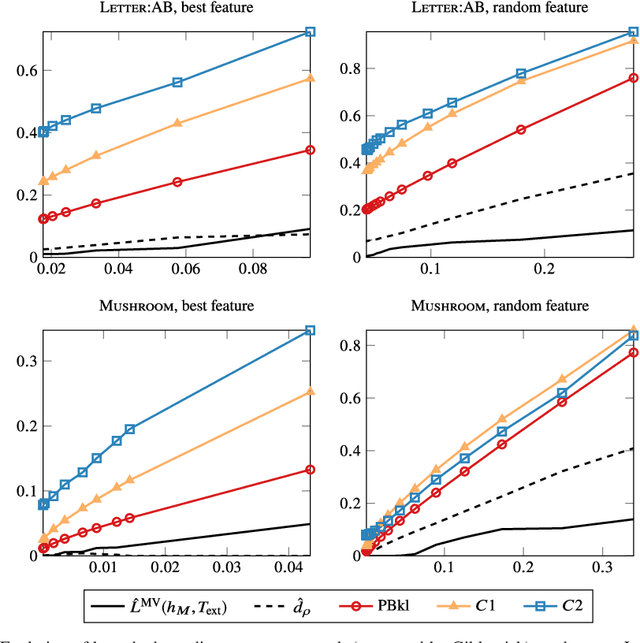
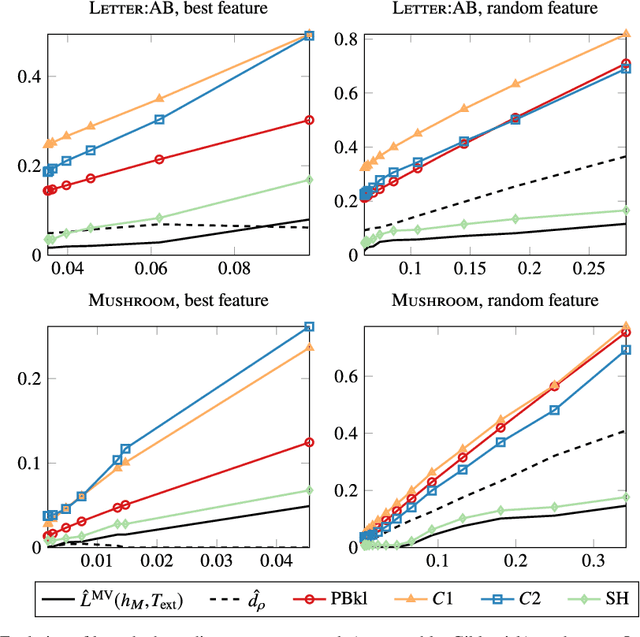
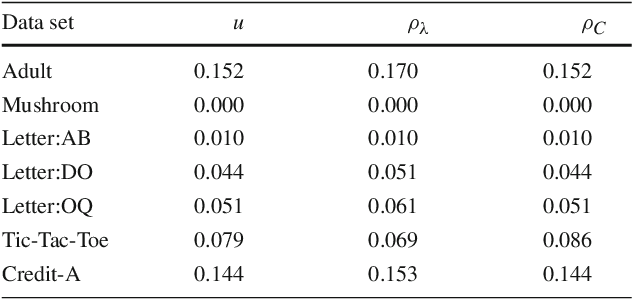
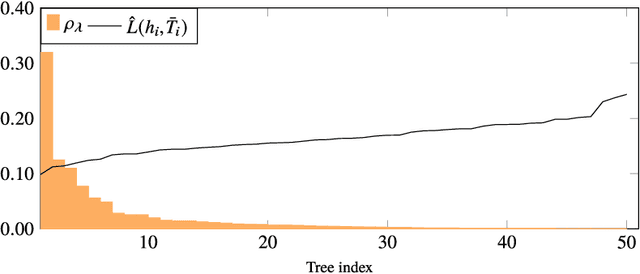
Existing guarantees in terms of rigorous upper bounds on the generalization error for the original random forest algorithm, one of the most frequently used machine learning methods, are unsatisfying. We discuss and evaluate various PAC-Bayesian approaches to derive such bounds. The bounds do not require additional hold-out data, because the out-of-bag samples from the bagging in the training process can be exploited. A random forest predicts by taking a majority vote of an ensemble of decision trees. The first approach is to bound the error of the vote by twice the error of the corresponding Gibbs classifier (classifying with a single member of the ensemble selected at random). However, this approach does not take into account the effect of averaging out of errors of individual classifiers when taking the majority vote. This effect provides a significant boost in performance when the errors are independent or negatively correlated, but when the correlations are strong the advantage from taking the majority vote is small. The second approach based on PAC-Bayesian C-bounds takes dependencies between ensemble members into account, but it requires estimating correlations between the errors of the individual classifiers. When the correlations are high or the estimation is poor, the bounds degrade. In our experiments, we compute generalization bounds for random forests on various benchmark data sets. Because the individual decision trees already perform well, their predictions are highly correlated and the C-bounds do not lead to satisfactory results. For the same reason, the bounds based on the analysis of Gibbs classifiers are typically superior and often reasonably tight. Bounds based on a validation set coming at the cost of a smaller training set gave better performance guarantees, but worse performance in most experiments.

PADDIT: Probabilistic Augmentation of Data using Diffeomorphic Image Transformation

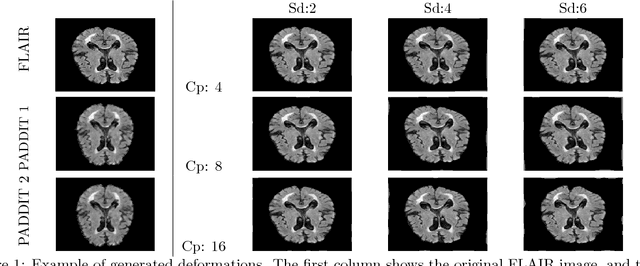
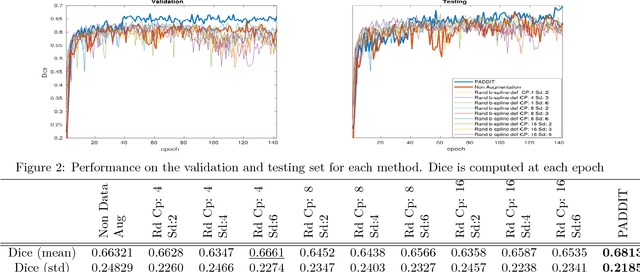
For proper generalization performance of convolutional neural networks (CNNs) in medical image segmentation, the learnt features should be invariant under particular non-linear shape variations of the input. To induce invariance in CNNs to such transformations, we propose Probabilistic Augmentation of Data using Diffeomorphic Image Transformation (PADDIT) -- a systematic framework for generating realistic transformations that can be used to augment data for training CNNs. We show that CNNs trained with PADDIT outperforms CNNs trained without augmentation and with generic augmentation in segmenting white matter hyperintensities from T1 and FLAIR brain MRI scans.

Training Big Random Forests with Little Resources

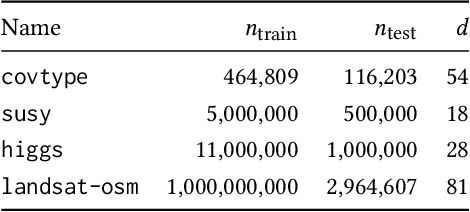
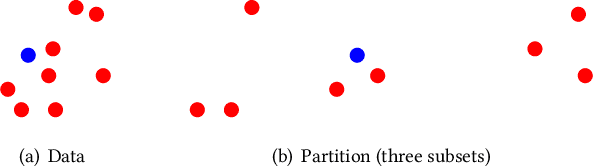
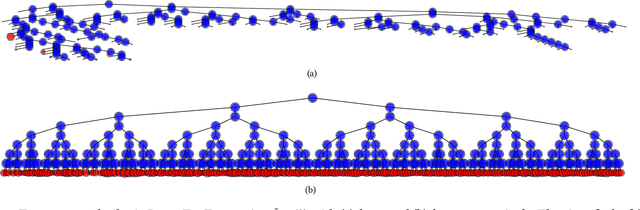
Without access to large compute clusters, building random forests on large datasets is still a challenging problem. This is, in particular, the case if fully-grown trees are desired. We propose a simple yet effective framework that allows to efficiently construct ensembles of huge trees for hundreds of millions or even billions of training instances using a cheap desktop computer with commodity hardware. The basic idea is to consider a multi-level construction scheme, which builds top trees for small random subsets of the available data and which subsequently distributes all training instances to the top trees' leaves for further processing. While being conceptually simple, the overall efficiency crucially depends on the particular implementation of the different phases. The practical merits of our approach are demonstrated using dense datasets with hundreds of millions of training instances.

A Strongly Quasiconvex PAC-Bayesian Bound

We propose a new PAC-Bayesian bound and a way of constructing a hypothesis space, so that the bound is convex in the posterior distribution and also convex in a trade-off parameter between empirical performance of the posterior distribution and its complexity. The complexity is measured by the Kullback-Leibler divergence to a prior. We derive an alternating procedure for minimizing the bound. We show that the bound can be rewritten as a one-dimensional function of the trade-off parameter and provide sufficient conditions under which the function has a single global minimum. When the conditions are satisfied the alternating minimization is guaranteed to converge to the global minimum of the bound. We provide experimental results demonstrating that rigorous minimization of the bound is competitive with cross-validation in tuning the trade-off between complexity and empirical performance. In all our experiments the trade-off turned to be quasiconvex even when the sufficient conditions were violated.