Recursive PAC-Bayes: A Frequentist Approach to Sequential Prior Updates with No Information Loss

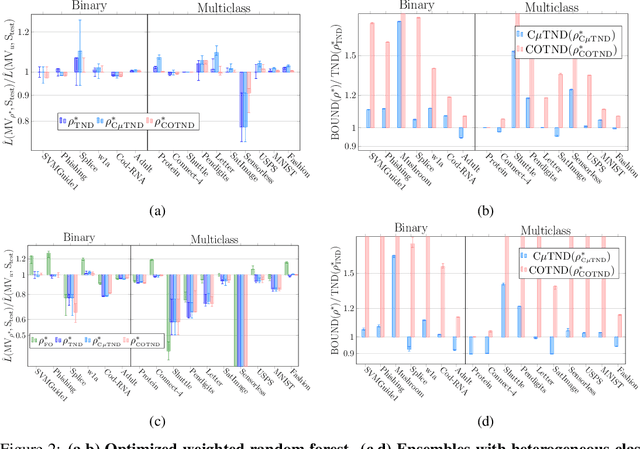
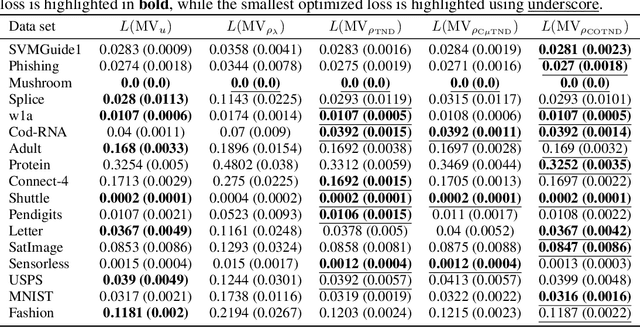
PAC-Bayesian analysis is a frequentist framework for incorporating prior knowledge into learning. It was inspired by Bayesian learning, which allows sequential data processing and naturally turns posteriors from one processing step into priors for the next. However, despite two and a half decades of research, the ability to update priors sequentially without losing confidence information along the way remained elusive for PAC-Bayes. While PAC-Bayes allows construction of data-informed priors, the final confidence intervals depend only on the number of points that were not used for the construction of the prior, whereas confidence information in the prior, which is related to the number of points used to construct the prior, is lost. This limits the possibility and benefit of sequential prior updates, because the final bounds depend only on the size of the final batch. We present a novel and, in retrospect, surprisingly simple and powerful PAC-Bayesian procedure that allows sequential prior updates with no information loss. The procedure is based on a novel decomposition of the expected loss of randomized classifiers. The decomposition rewrites the loss of the posterior as an excess loss relative to a downscaled loss of the prior plus the downscaled loss of the prior, which is bounded recursively. As a side result, we also present a generalization of the split-kl and PAC-Bayes-split-kl inequalities to discrete random variables, which we use for bounding the excess losses, and which can be of independent interest. In empirical evaluation the new procedure significantly outperforms state-of-the-art.

An Improved Best-of-both-worlds Algorithm for Bandits with Delayed Feedback

We propose a new best-of-both-worlds algorithm for bandits with variably delayed feedback. The algorithm improves on prior work by Masoudian et al. [2022] by eliminating the need in prior knowledge of the maximal delay $d_{\mathrm{max}}$ and providing tighter regret bounds in both regimes. The algorithm and its regret bounds are based on counts of outstanding observations (a quantity that is observed at action time) rather than delays or the maximal delay (quantities that are only observed when feedback arrives). One major contribution is a novel control of distribution drift, which is based on biased loss estimators and skipping of observations with excessively large delays. Another major contribution is demonstrating that the complexity of best-of-both-worlds bandits with delayed feedback is characterized by the cumulative count of outstanding observations after skipping of observations with excessively large delays, rather than the delays or the maximal delay.

Delayed Bandits: When Do Intermediate Observations Help?

We study a $K$-armed bandit with delayed feedback and intermediate observations. We consider a model where intermediate observations have a form of a finite state, which is observed immediately after taking an action, whereas the loss is observed after an adversarially chosen delay. We show that the regime of the mapping of states to losses determines the complexity of the problem, irrespective of whether the mapping of actions to states is stochastic or adversarial. If the mapping of states to losses is adversarial, then the regret rate is of order $\sqrt{(K+d)T}$ (within log factors), where $T$ is the time horizon and $d$ is a fixed delay. This matches the regret rate of a $K$-armed bandit with delayed feedback and without intermediate observations, implying that intermediate observations are not helpful. However, if the mapping of states to losses is stochastic, we show that the regret grows at a rate of $\sqrt{\big(K+\min\{|\mathcal{S}|,d\}\big)T}$ (within log factors), implying that if the number $|\mathcal{S}|$ of states is smaller than the delay, then intermediate observations help. We also provide refined high-probability regret upper bounds for non-uniform delays, together with experimental validation of our algorithms.

A Best-of-Both-Worlds Algorithm for Bandits with Delayed Feedback

We present a modified tuning of the algorithm of Zimmert and Seldin [2020] for adversarial multiarmed bandits with delayed feedback, which in addition to the minimax optimal adversarial regret guarantee shown by Zimmert and Seldin simultaneously achieves a near-optimal regret guarantee in the stochastic setting with fixed delays. Specifically, the adversarial regret guarantee is $\mathcal{O}(\sqrt{TK} + \sqrt{dT\log K})$, where $T$ is the time horizon, $K$ is the number of arms, and $d$ is the fixed delay, whereas the stochastic regret guarantee is $\mathcal{O}\left(\sum_{i \neq i^*}(\frac{1}{\Delta_i} \log(T) + \frac{d}{\Delta_{i}\log K}) + d K^{1/3}\log K\right)$, where $\Delta_i$ are the suboptimality gaps. We also present an extension of the algorithm to the case of arbitrary delays, which is based on an oracle knowledge of the maximal delay $d_{max}$ and achieves $\mathcal{O}(\sqrt{TK} + \sqrt{D\log K} + d_{max}K^{1/3} \log K)$ regret in the adversarial regime, where $D$ is the total delay, and $\mathcal{O}\left(\sum_{i \neq i^*}(\frac{1}{\Delta_i} \log(T) + \frac{\sigma_{max}}{\Delta_{i}\log K}) + d_{max}K^{1/3}\log K\right)$ regret in the stochastic regime, where $\sigma_{max}$ is the maximal number of outstanding observations. Finally, we present a lower bound that matches regret upper bound achieved by the skipping technique of Zimmert and Seldin [2020] in the adversarial setting.

Split-kl and PAC-Bayes-split-kl Inequalities

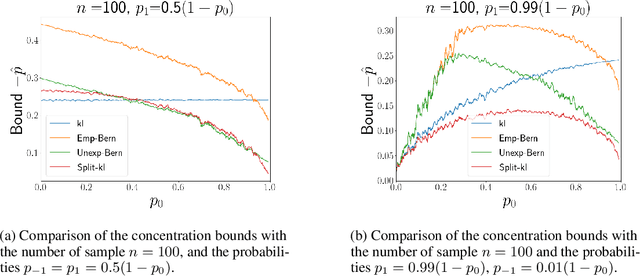
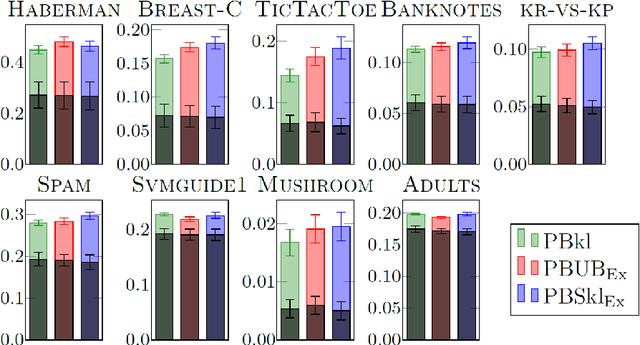
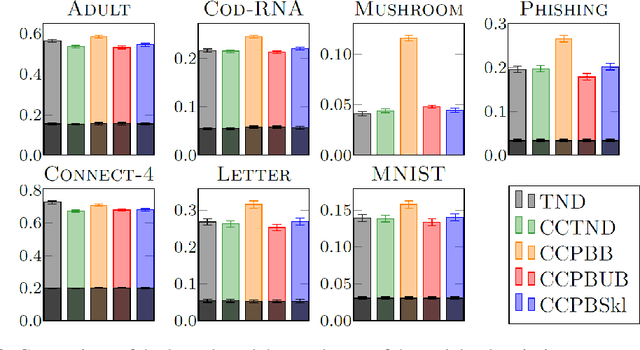
We present a new concentration of measure inequality for sums of independent bounded random variables, which we name a split-kl inequality. The inequality combines the combinatorial power of the kl inequality with ability to exploit low variance. While for Bernoulli random variables the kl inequality is tighter than the Empirical Bernstein, for random variables taking values inside a bounded interval and having low variance the Empirical Bernstein inequality is tighter than the kl. The proposed split-kl inequality yields the best of both worlds. We discuss an application of the split-kl inequality to bounding excess losses. We also derive a PAC-Bayes-split-kl inequality and use a synthetic example and several UCI datasets to compare it with the PAC-Bayes-kl, PAC-Bayes Empirical Bernstein, PAC-Bayes Unexpected Bernstein, and PAC-Bayes Empirical Bennett inequalities.

A Near-Optimal Best-of-Both-Worlds Algorithm for Online Learning with Feedback Graphs

We consider online learning with feedback graphs, a sequential decision-making framework where the learner's feedback is determined by a directed graph over the action set. We present a computationally efficient algorithm for learning in this framework that simultaneously achieves near-optimal regret bounds in both stochastic and adversarial environments. The bound against oblivious adversaries is $\tilde{O} (\sqrt{\alpha T})$, where $T$ is the time horizon and $\alpha$ is the independence number of the feedback graph. The bound against stochastic environments is $O\big( (\ln T)^2 \max_{S\in \mathcal I(G)} \sum_{i \in S} \Delta_i^{-1}\big)$ where $\mathcal I(G)$ is the family of all independent sets in a suitably defined undirected version of the graph and $\Delta_i$ are the suboptimality gaps. The algorithm combines ideas from the EXP3++ algorithm for stochastic and adversarial bandits and the EXP3.G algorithm for feedback graphs with a novel exploration scheme. The scheme, which exploits the structure of the graph to reduce exploration, is key to obtain best-of-both-worlds guarantees with feedback graphs. We also extend our algorithm and results to a setting where the feedback graphs are allowed to change over time.

Chebyshev-Cantelli PAC-Bayes-Bennett Inequality for the Weighted Majority Vote

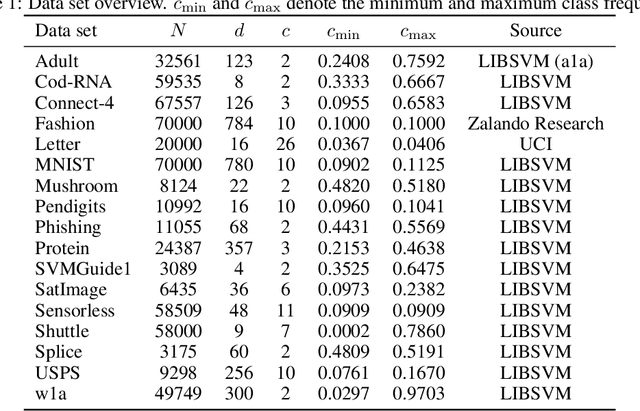
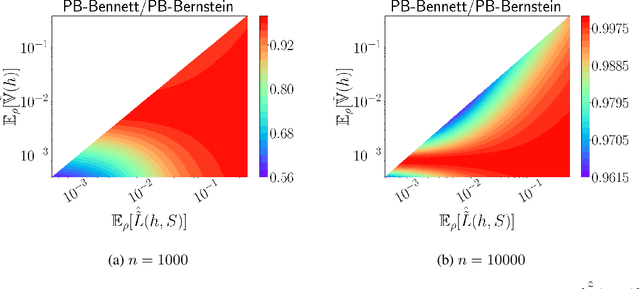
We present a new second-order oracle bound for the expected risk of a weighted majority vote. The bound is based on a novel parametric form of the Chebyshev-Cantelli inequality (a.k.a.\ one-sided Chebyshev's), which is amenable to efficient minimization. The new form resolves the optimization challenge faced by prior oracle bounds based on the Chebyshev-Cantelli inequality, the C-bounds [Germain et al., 2015], and, at the same time, it improves on the oracle bound based on second order Markov's inequality introduced by Masegosa et al. [2020]. We also derive the PAC-Bayes-Bennett inequality, which we use for empirical estimation of the oracle bound. The PAC-Bayes-Bennett inequality improves on the PAC-Bayes-Bernstein inequality by Seldin et al. [2012]. We provide an empirical evaluation demonstrating that the new bounds can improve on the work by Masegosa et al. [2020]. Both the parametric form of the Chebyshev-Cantelli inequality and the PAC-Bayes-Bennett inequality may be of independent interest for the study of concentration of measure in other domains.

Improved Analysis of Robustness of the Tsallis-INF Algorithm to Adversarial Corruptions in Stochastic Multiarmed Bandits

We derive improved regret bounds for the Tsallis-INF algorithm of Zimmert and Seldin (2021). In the adversarial regime with a self-bounding constraint and the stochastic regime with adversarial corruptions as its special case we improve the dependence on corruption magnitude $C$. In particular, for $C = \Theta\left(\frac{T}{\log T}\right)$, where $T$ is the time horizon, we achieve an improvement by a multiplicative factor of $\sqrt{\frac{\log T}{\log\log T}}$ relative to the bound of Zimmert and Seldin (2021). We also improve the dependence of the regret bound on time horizon from $\log T$ to $\log \frac{(K-1)T}{(\sum_{i\neq i^*}\frac{1}{\Delta_i})^2}$, where $K$ is the number of arms, $\Delta_i$ are suboptimality gaps for suboptimal arms $i$, and $i^*$ is the optimal arm. Additionally, we provide a general analysis, which allows to achieve the same kind of improvement for generalizations of Tsallis-INF to other settings beyond multiarmed bandits.

An Algorithm for Stochastic and Adversarial Bandits with Switching Costs

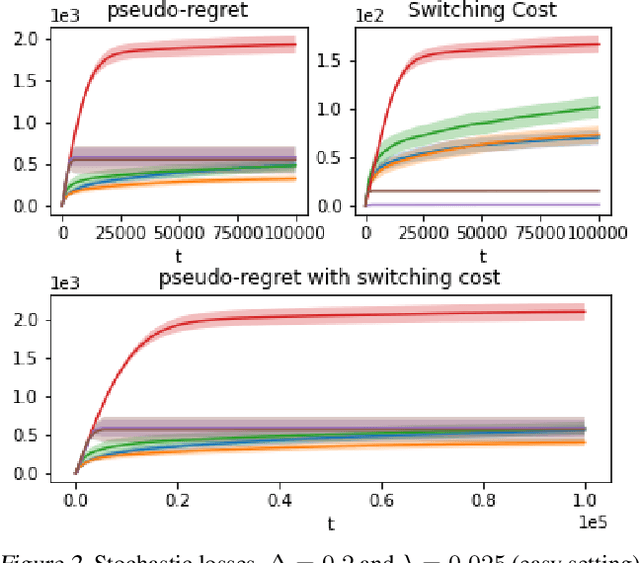
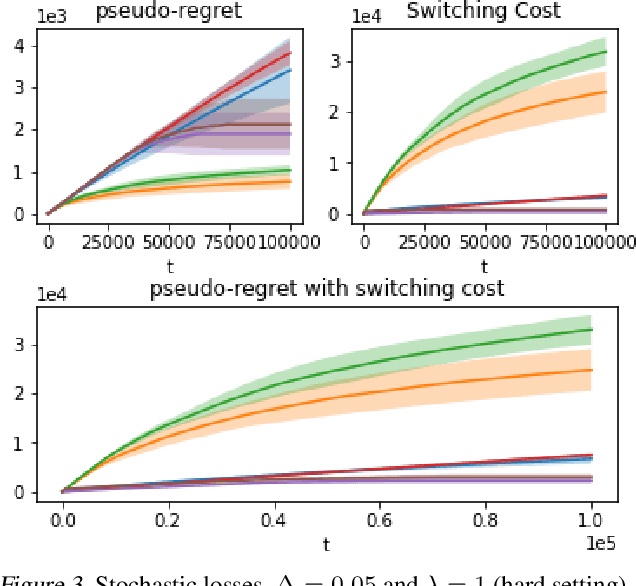
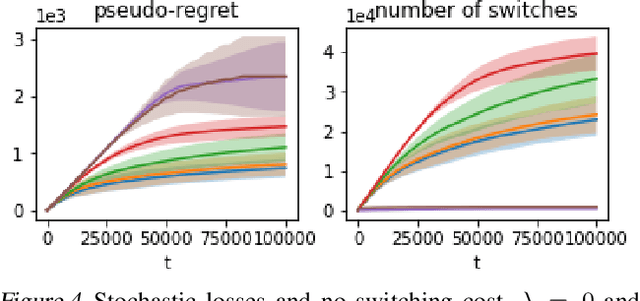
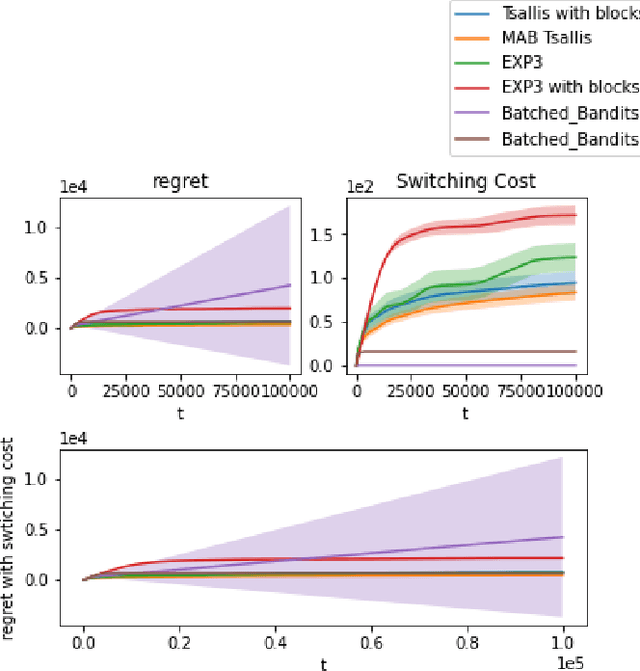
We propose an algorithm for stochastic and adversarial multiarmed bandits with switching costs, where the algorithm pays a price $\lambda$ every time it switches the arm being played. Our algorithm is based on adaptation of the Tsallis-INF algorithm of Zimmert and Seldin (2021) and requires no prior knowledge of the regime or time horizon. In the oblivious adversarial setting it achieves the minimax optimal regret bound of $O\big((\lambda K)^{1/3}T^{2/3} + \sqrt{KT}\big)$, where $T$ is the time horizon and $K$ is the number of arms. In the stochastically constrained adversarial regime, which includes the stochastic regime as a special case, it achieves a regret bound of $O\left(\big((\lambda K)^{2/3} T^{1/3} + \ln T\big)\sum_{i \neq i^*} \Delta_i^{-1}\right)$, where $\Delta_i$ are the suboptimality gaps and $i^*$ is a unique optimal arm. In the special case of $\lambda = 0$ (no switching costs), both bounds are minimax optimal within constants. We also explore variants of the problem, where switching cost is allowed to change over time. We provide experimental evaluation showing competitiveness of our algorithm with the relevant baselines in the stochastic, stochastically constrained adversarial, and adversarial regimes with fixed switching cost.

An Optimal Algorithm for Adversarial Bandits with Arbitrary Delays

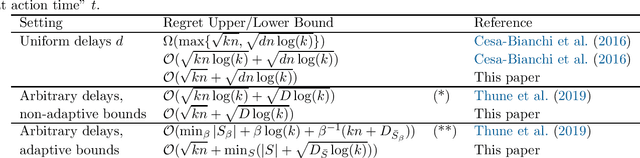
We propose a new algorithm for adversarial multi-armed bandits with unrestricted delays. The algorithm is based on a novel hybrid regularizer applied in the Follow the Regularized Leader (FTRL) framework. It achieves $\mathcal{O}(\sqrt{kn}+\sqrt{D\log(k)})$ regret guarantee, where $k$ is the number of arms, $n$ is the number of rounds, and $D$ is the total delay. The result matches the lower bound within constants and requires no prior knowledge of $n$ or $D$. Additionally, we propose a refined tuning of the algorithm, which achieves $\mathcal{O}(\sqrt{kn}+\min_{S}|S|+\sqrt{D_{\bar S}\log(k)})$ regret guarantee, where $S$ is a set of rounds excluded from delay counting, $\bar S = [n]\setminus S$ are the counted rounds, and $D_{\bar S}$ is the total delay in the counted rounds. If the delays are highly unbalanced, the latter regret guarantee can be significantly tighter than the former. The result requires no advance knowledge of the delays and resolves an open problem of Thune et al. (2019). The new FTRL algorithm and its refined tuning are anytime and require no doubling, which resolves another open problem of Thune et al. (2019).