Stephan Sloth Lorenzen
Information Bottleneck: Exact Analysis of (Quantized) Neural Networks
Jun 24, 2021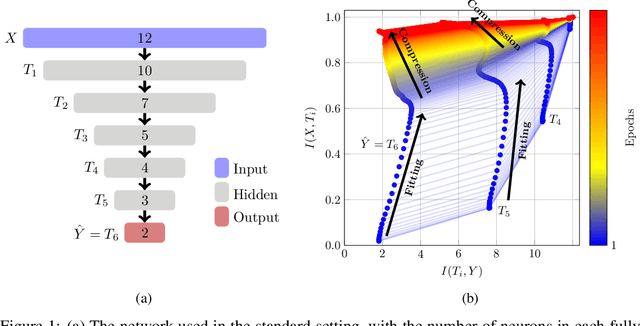
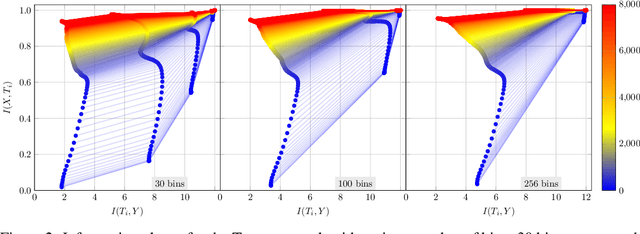
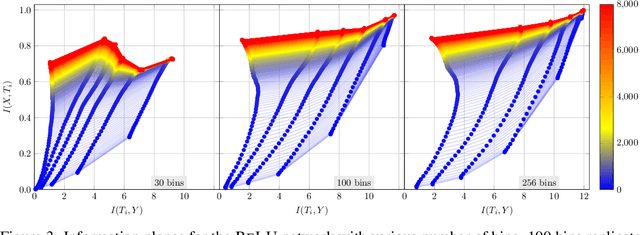
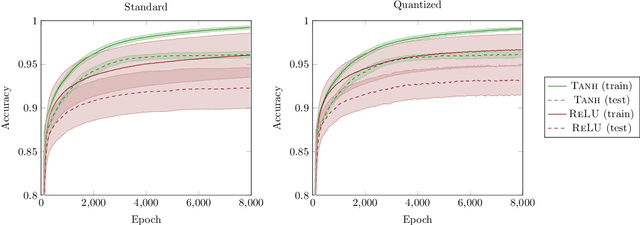
Abstract:The information bottleneck (IB) principle has been suggested as a way to analyze deep neural networks. The learning dynamics are studied by inspecting the mutual information (MI) between the hidden layers and the input and output. Notably, separate fitting and compression phases during training have been reported. This led to some controversy including claims that the observations are not reproducible and strongly dependent on the type of activation function used as well as on the way the MI is estimated. Our study confirms that different ways of binning when computing the MI lead to qualitatively different results, either supporting or refusing IB conjectures. To resolve the controversy, we study the IB principle in settings where MI is non-trivial and can be computed exactly. We monitor the dynamics of quantized neural networks, that is, we discretize the whole deep learning system so that no approximation is required when computing the MI. This allows us to quantify the information flow without measurement errors. In this setting, we observed a fitting phase for all layers and a compression phase for the output layer in all experiments; the compression in the hidden layers was dependent on the type of activation function. Our study shows that the initial IB results were not artifacts of binning when computing the MI. However, the critical claim that the compression phase may not be observed for some networks also holds true.
On PAC-Bayesian Bounds for Random Forests
Oct 23, 2018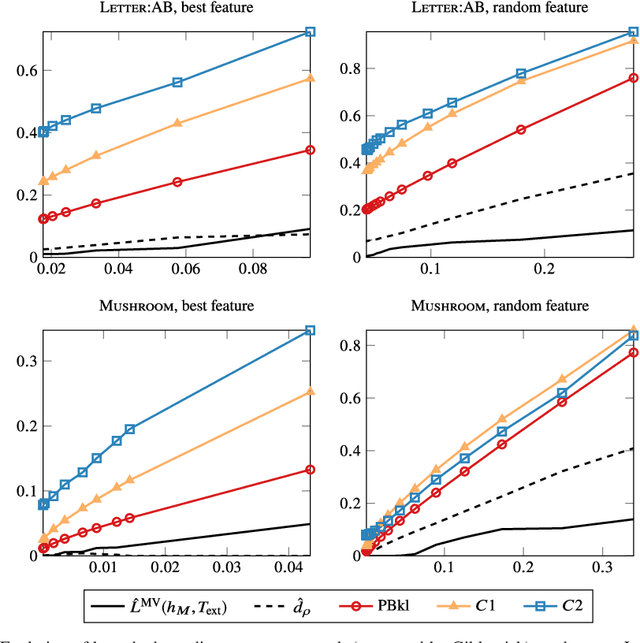
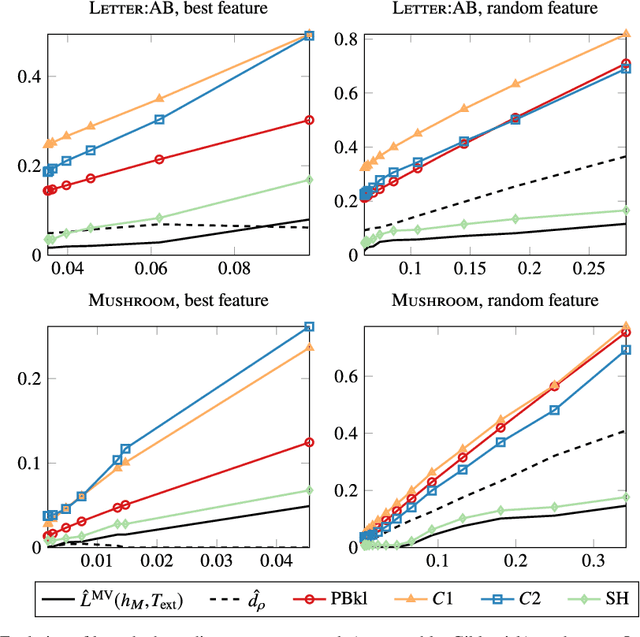
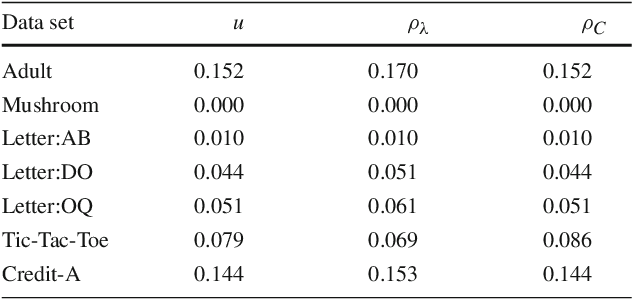
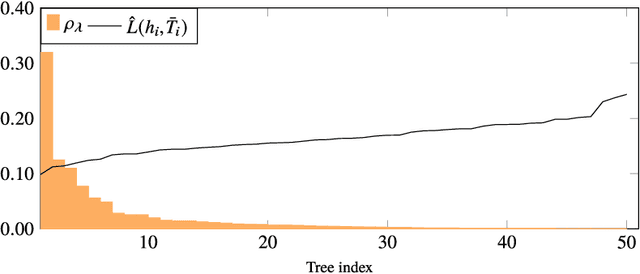
Abstract:Existing guarantees in terms of rigorous upper bounds on the generalization error for the original random forest algorithm, one of the most frequently used machine learning methods, are unsatisfying. We discuss and evaluate various PAC-Bayesian approaches to derive such bounds. The bounds do not require additional hold-out data, because the out-of-bag samples from the bagging in the training process can be exploited. A random forest predicts by taking a majority vote of an ensemble of decision trees. The first approach is to bound the error of the vote by twice the error of the corresponding Gibbs classifier (classifying with a single member of the ensemble selected at random). However, this approach does not take into account the effect of averaging out of errors of individual classifiers when taking the majority vote. This effect provides a significant boost in performance when the errors are independent or negatively correlated, but when the correlations are strong the advantage from taking the majority vote is small. The second approach based on PAC-Bayesian C-bounds takes dependencies between ensemble members into account, but it requires estimating correlations between the errors of the individual classifiers. When the correlations are high or the estimation is poor, the bounds degrade. In our experiments, we compute generalization bounds for random forests on various benchmark data sets. Because the individual decision trees already perform well, their predictions are highly correlated and the C-bounds do not lead to satisfactory results. For the same reason, the bounds based on the analysis of Gibbs classifiers are typically superior and often reasonably tight. Bounds based on a validation set coming at the cost of a smaller training set gave better performance guarantees, but worse performance in most experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge