Learning Diverse and Discriminative Representations via the Principle of Maximal Coding Rate Reduction

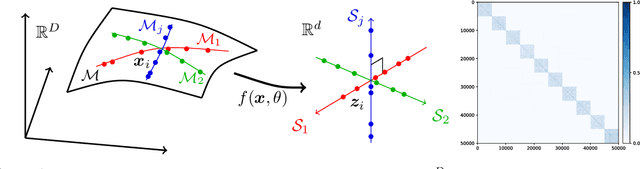
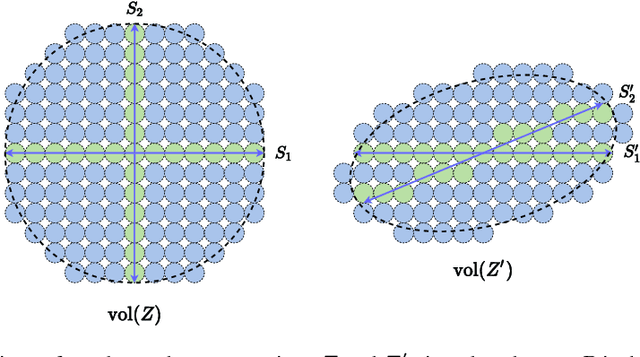
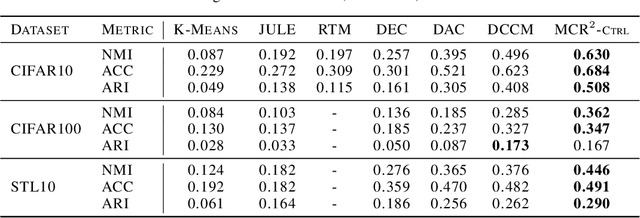
To learn intrinsic low-dimensional structures from high-dimensional data that most discriminate between classes, we propose the principle of Maximal Coding Rate Reduction ($\text{MCR}^2$), an information-theoretic measure that maximizes the coding rate difference between the whole dataset and the sum of each individual class. We clarify its relationships with most existing frameworks such as cross-entropy, information bottleneck, information gain, contractive and contrastive learning, and provide theoretical guarantees for learning diverse and discriminative features. The coding rate can be accurately computed from finite samples of degenerate subspace-like distributions and can learn intrinsic representations in supervised, self-supervised, and unsupervised settings in a unified manner. Empirically, the representations learned using this principle alone are significantly more robust to label corruptions in classification than those using cross-entropy, and can lead to state-of-the-art results in clustering mixed data from self-learned invariant features.

Recovery and Generalization in Over-Realized Dictionary Learning

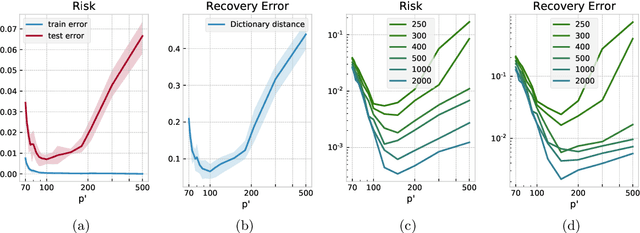
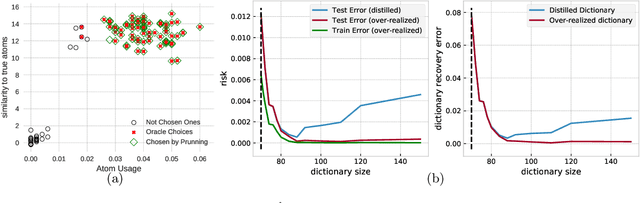
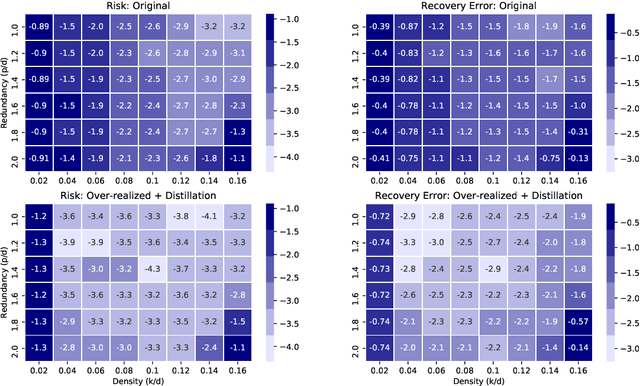
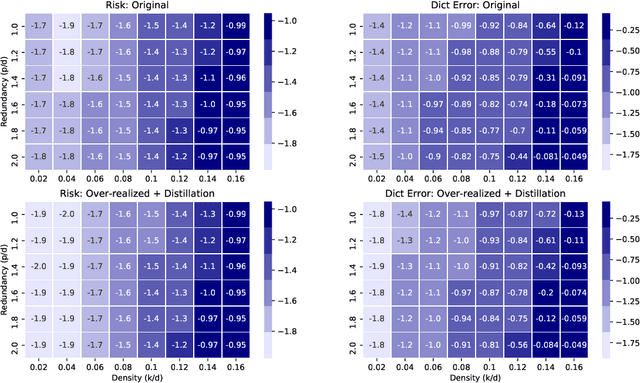
In over two decades of research, the field of dictionary learning has gathered a large collection of successful applications, and theoretical guarantees for model recovery are known only whenever optimization is carried out in the same model class as that of the underlying dictionary. This work characterizes the surprising phenomenon that dictionary recovery can be facilitated by searching over the space of larger over-realized models. This observation is general and independent of the specific dictionary learning algorithm used. We thoroughly demonstrate this observation in practice and provide a theoretical analysis of this phenomenon by tying recovery measures to generalization bounds. We further show that an efficient and provably correct distillation mechanism can be employed to recover the correct atoms from the over-realized model. As a result, our meta-algorithm provides dictionary estimates with consistently better recovery of the ground-truth model.

Self-Representation Based Unsupervised Exemplar Selection in a Union of Subspaces

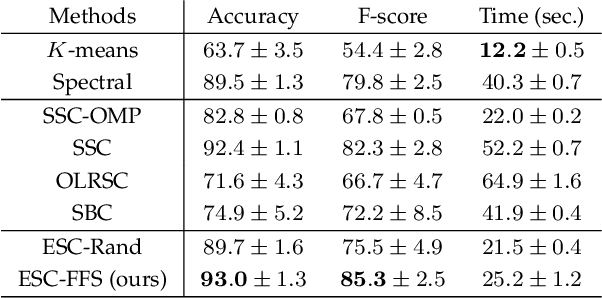
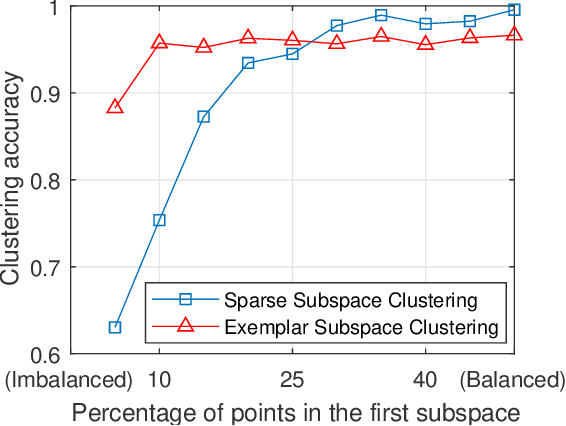
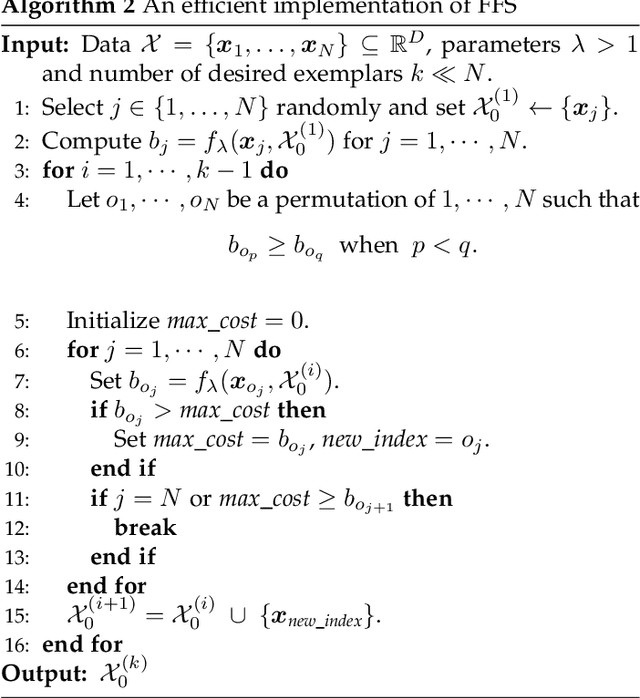
Finding a small set of representatives from an unlabeled dataset is a core problem in a broad range of applications such as dataset summarization and information extraction. Classical exemplar selection methods such as $k$-medoids work under the assumption that the data points are close to a few cluster centroids, and cannot handle the case where data lie close to a union of subspaces. This paper proposes a new exemplar selection model that searches for a subset that best reconstructs all data points as measured by the $\ell_1$ norm of the representation coefficients. Geometrically, this subset best covers all the data points as measured by the Minkowski functional of the subset. To solve our model efficiently, we introduce a farthest first search algorithm that iteratively selects the worst represented point as an exemplar. When the dataset is drawn from a union of independent subspaces, our method is able to select sufficiently many representatives from each subspace. We further develop an exemplar based subspace clustering method that is robust to imbalanced data and efficient for large scale data. Moreover, we show that a classifier trained on the selected exemplars (when they are labeled) can correctly classify the rest of the data points.

Is an Affine Constraint Needed for Affine Subspace Clustering?

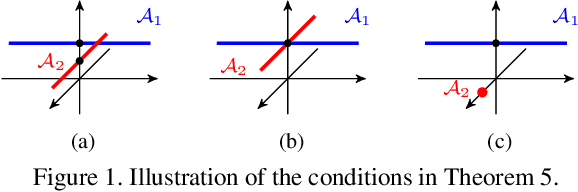
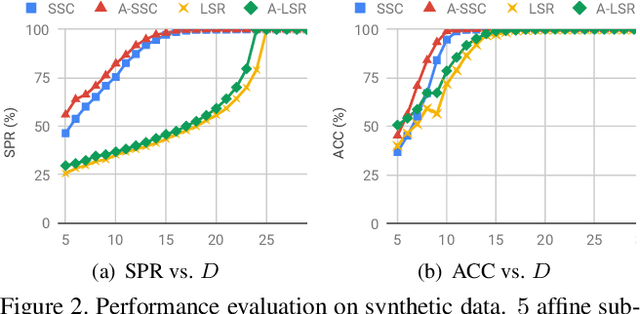
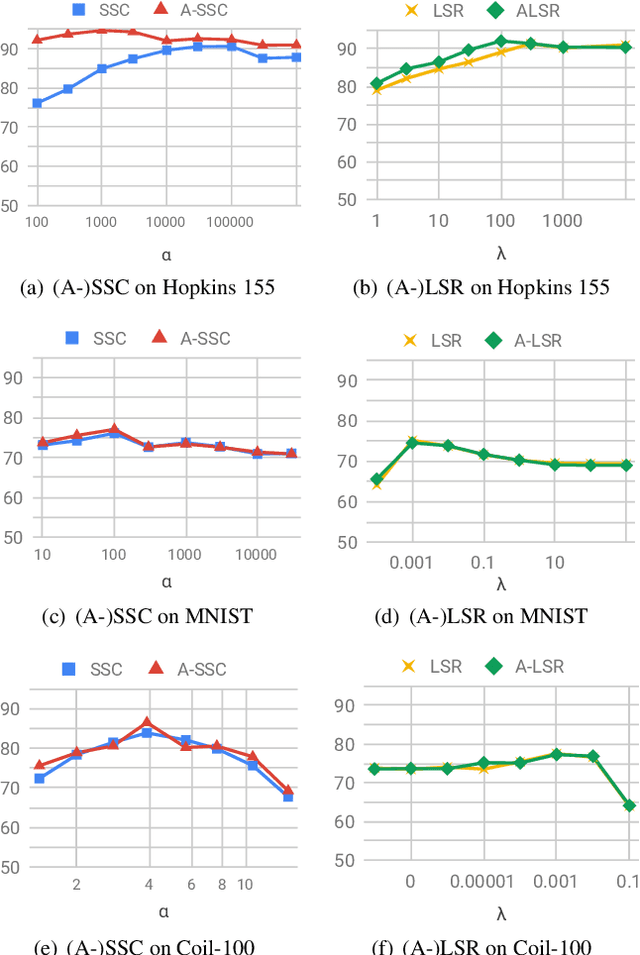
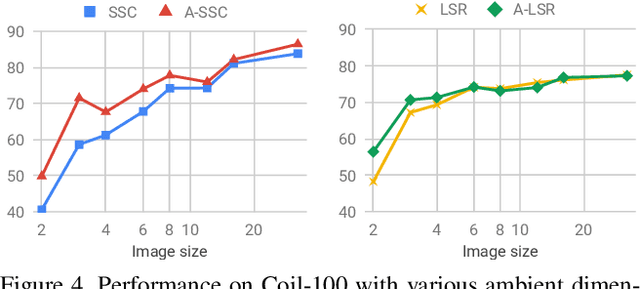
Subspace clustering methods based on expressing each data point as a linear combination of other data points have achieved great success in computer vision applications such as motion segmentation, face and digit clustering. In face clustering, the subspaces are linear and subspace clustering methods can be applied directly. In motion segmentation, the subspaces are affine and an additional affine constraint on the coefficients is often enforced. However, since affine subspaces can always be embedded into linear subspaces of one extra dimension, it is unclear if the affine constraint is really necessary. This paper shows, both theoretically and empirically, that when the dimension of the ambient space is high relative to the sum of the dimensions of the affine subspaces, the affine constraint has a negligible effect on clustering performance. Specifically, our analysis provides conditions that guarantee the correctness of affine subspace clustering methods both with and without the affine constraint, and shows that these conditions are satisfied for high-dimensional data. Underlying our analysis is the notion of affinely independent subspaces, which not only provides geometrically interpretable correctness conditions, but also clarifies the relationships between existing results for affine subspace clustering.

Stochastic Sparse Subspace Clustering

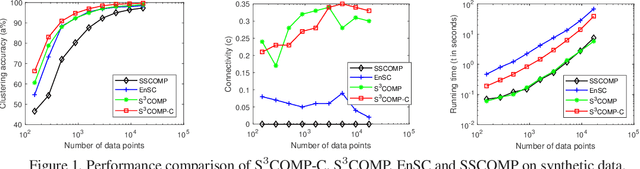
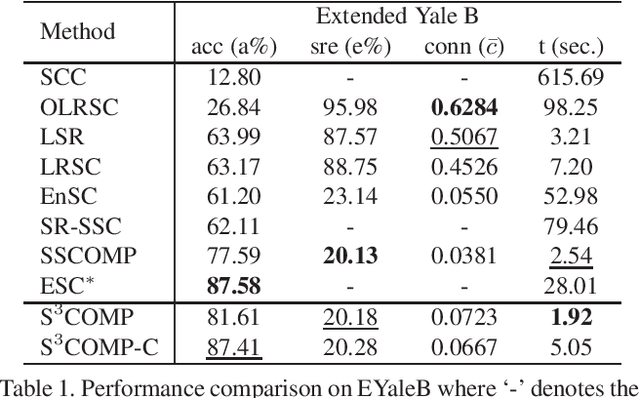
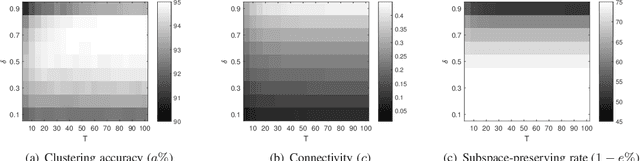
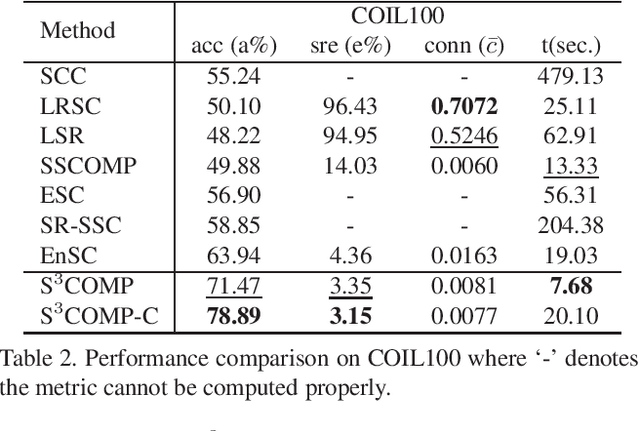
State-of-the-art subspace clustering methods are based on self-expressive model, which represents each data point as a linear combination of other data points. By enforcing such representation to be sparse, sparse subspace clustering is guaranteed to produce a subspace-preserving data affinity where two points are connected only if they are from the same subspace. On the other hand, however, data points from the same subspace may not be well-connected, leading to the issue of over-segmentation. We introduce dropout to address the issue of over-segmentation, which is based on randomly dropping out data points in self-expressive model. In particular, we show that dropout is equivalent to adding a squared $\ell_2$ norm regularization on the representation coefficients, therefore induces denser solutions. Then, we reformulate the optimization problem as a consensus problem over a set of small-scale subproblems. This leads to a scalable and flexible sparse subspace clustering approach, termed Stochastic Sparse Subspace Clustering, which can effectively handle large scale datasets. Extensive experiments on synthetic data and real world datasets validate the efficiency and effectiveness of our proposal.

Rethinking Bias-Variance Trade-off for Generalization of Neural Networks

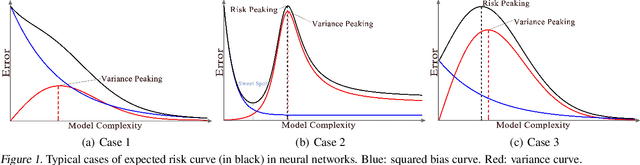
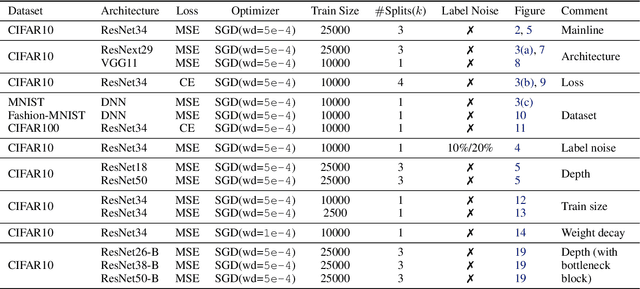
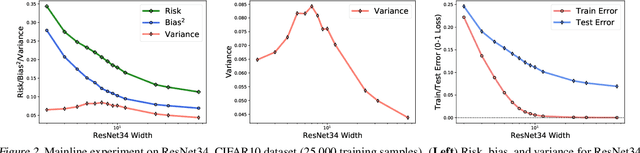
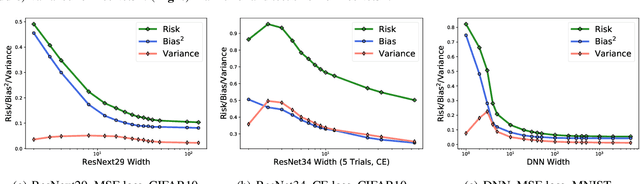
The classical bias-variance trade-off predicts that bias decreases and variance increase with model complexity, leading to a U-shaped risk curve. Recent work calls this into question for neural networks and other over-parameterized models, for which it is often observed that larger models generalize better. We provide a simple explanation for this by measuring the bias and variance of neural networks: while the bias is monotonically decreasing as in the classical theory, the variance is unimodal or bell-shaped: it increases then decreases with the width of the network. We vary the network architecture, loss function, and choice of dataset and confirm that variance unimodality occurs robustly for all models we considered. The risk curve is the sum of the bias and variance curves and displays different qualitative shapes depending on the relative scale of bias and variance, with the double descent curve observed in recent literature as a special case. We corroborate these empirical results with a theoretical analysis of two-layer linear networks with random first layer. Finally, evaluation on out-of-distribution data shows that most of the drop in accuracy comes from increased bias while variance increases by a relatively small amount. Moreover, we find that deeper models decrease bias and increase variance for both in-distribution and out-of-distribution data.

Basis Pursuit and Orthogonal Matching Pursuit for Subspace-preserving Recovery: Theoretical Analysis

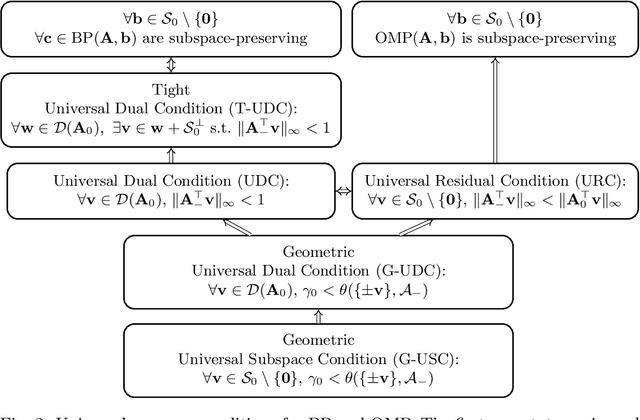
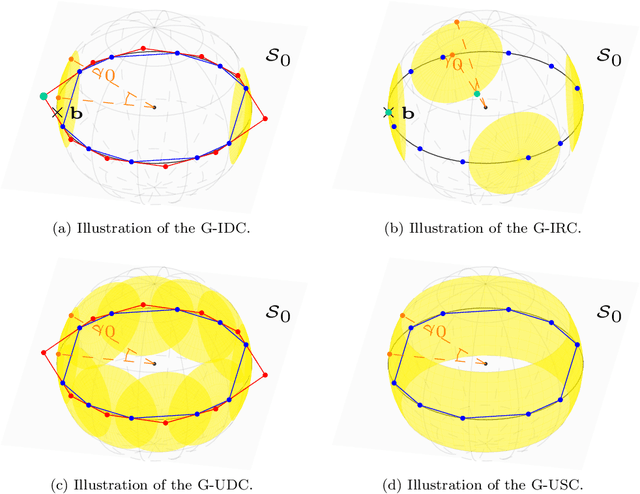
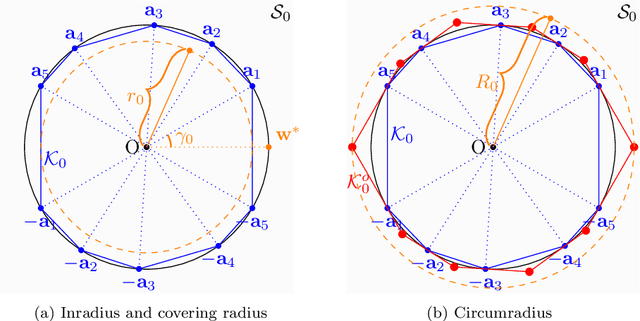
Given an overcomplete dictionary $A$ and a signal $b = Ac^*$ for some sparse vector $c^*$ whose nonzero entries correspond to linearly independent columns of $A$, classical sparse signal recovery theory considers the problem of whether $c^*$ can be recovered as the unique sparsest solution to $b = A c$. It is now well-understood that such recovery is possible by practical algorithms when the dictionary $A$ is incoherent or restricted isometric. In this paper, we consider the more general case where $b$ lies in a subspace $\mathcal{S}_0$ spanned by a subset of linearly dependent columns of $A$, and the remaining columns are outside of the subspace. In this case, the sparsest representation may not be unique, and the dictionary may not be incoherent or restricted isometric. The goal is to have the representation $c$ correctly identify the subspace, i.e. the nonzero entries of $c$ should correspond to columns of $A$ that are in the subspace $\mathcal{S}_0$. Such a representation $c$ is called subspace-preserving, a key concept that has found important applications for learning low-dimensional structures in high-dimensional data. We present various geometric conditions that guarantee subspace-preserving recovery. Among them, the major results are characterized by the covering radius and the angular distance, which capture the distribution of points in the subspace and the similarity between points in the subspace and points outside the subspace, respectively. Importantly, these conditions do not require the dictionary to be incoherent or restricted isometric. By establishing that the subspace-preserving recovery problem and the classical sparse signal recovery problem are equivalent under common assumptions on the latter, we show that several of our proposed conditions are generalizations of some well-known conditions in the sparse signal recovery literature.

Self-Supervised Convolutional Subspace Clustering Network

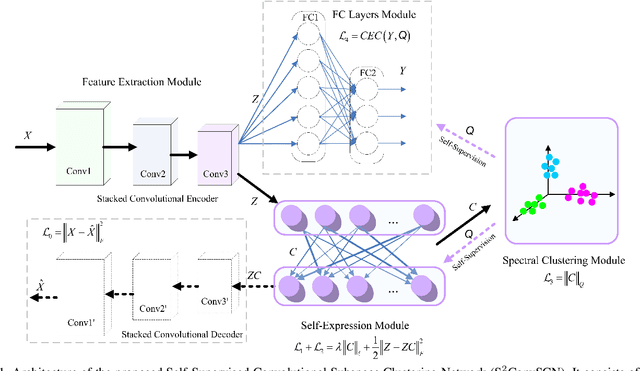
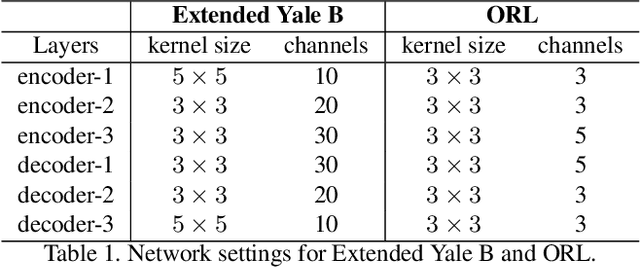
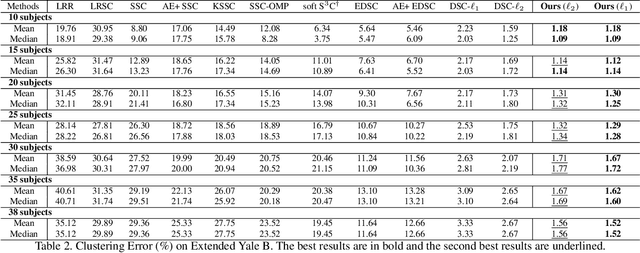
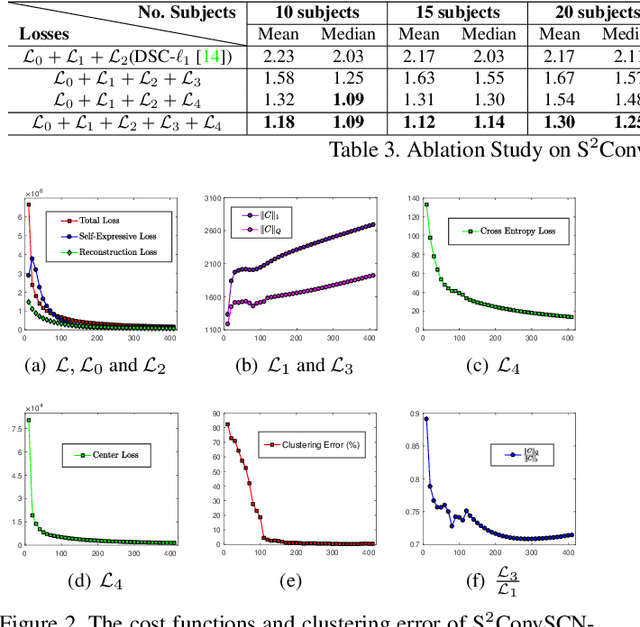
Subspace clustering methods based on data self-expression have become very popular for learning from data that lie in a union of low-dimensional linear subspaces. However, the applicability of subspace clustering has been limited because practical visual data in raw form do not necessarily lie in such linear subspaces. On the other hand, while Convolutional Neural Network (ConvNet) has been demonstrated to be a powerful tool for extracting discriminative features from visual data, training such a ConvNet usually requires a large amount of labeled data, which are unavailable in subspace clustering applications. To achieve simultaneous feature learning and subspace clustering, we propose an end-to-end trainable framework, called Self-Supervised Convolutional Subspace Clustering Network (S$^2$ConvSCN), that combines a ConvNet module (for feature learning), a self-expression module (for subspace clustering) and a spectral clustering module (for self-supervision) into a joint optimization framework. Particularly, we introduce a dual self-supervision that exploits the output of spectral clustering to supervise the training of the feature learning module (via a classification loss) and the self-expression module (via a spectral clustering loss). Our experiments on four benchmark datasets show the effectiveness of the dual self-supervision and demonstrate superior performance of our proposed approach.

On Geometric Analysis of Affine Sparse Subspace Clustering

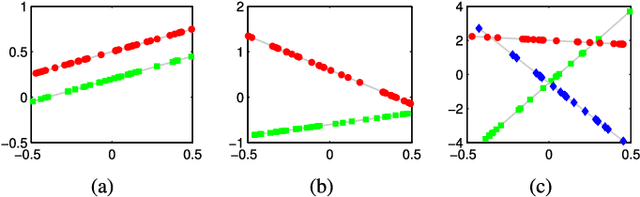
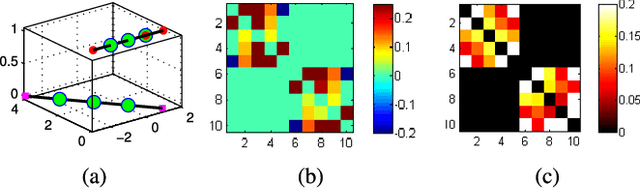
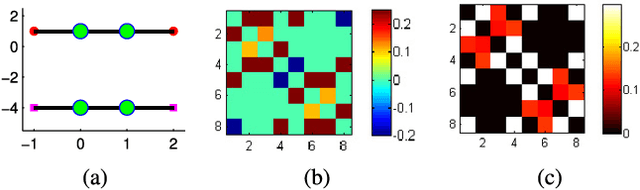
Sparse subspace clustering (SSC) is a state-of-the-art method for segmenting a set of data points drawn from a union of subspaces into their respective subspaces. It is now well understood that SSC produces subspace-preserving data affinity under broad geometric conditions but suffers from a connectivity issue. In this paper, we develop a novel geometric analysis for a variant of SSC, named affine SSC (ASSC), for the problem of clustering data from a union of affine subspaces. Our contributions include a new concept called affine independence for capturing the arrangement of a collection of affine subspaces. Under the affine independence assumption, we show that ASSC is guaranteed to produce subspace-preserving affinity. Moreover, inspired by the phenomenon that the $\ell_1$ regularization no longer induces sparsity when the solution is nonnegative, we further show that subspace-preserving recovery can be achieved under much weaker conditions for all data points other than the extreme points of samples from each subspace. In addition, we confirm a curious observation that the affinity produced by ASSC may be subspace-dense---which could guarantee the subspace-preserving affinity of ASSC to produce correct clustering under rather weak conditions. We validate the theoretical findings on carefully designed synthetic data and evaluate the performance of ASSC on several real data sets.

Provable Self-Representation Based Outlier Detection in a Union of Subspaces

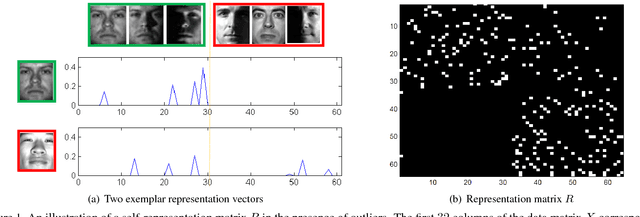
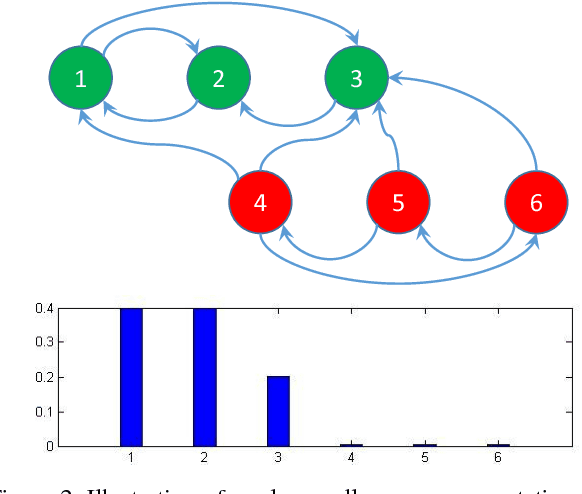
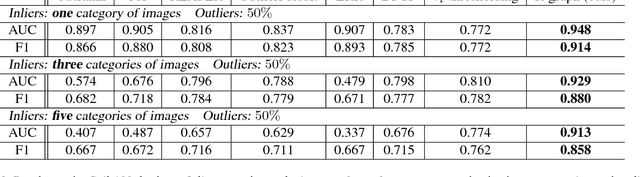
Many computer vision tasks involve processing large amounts of data contaminated by outliers, which need to be detected and rejected. While outlier detection methods based on robust statistics have existed for decades, only recently have methods based on sparse and low-rank representation been developed along with guarantees of correct outlier detection when the inliers lie in one or more low-dimensional subspaces. This paper proposes a new outlier detection method that combines tools from sparse representation with random walks on a graph. By exploiting the property that data points can be expressed as sparse linear combinations of each other, we obtain an asymmetric affinity matrix among data points, which we use to construct a weighted directed graph. By defining a suitable Markov Chain from this graph, we establish a connection between inliers/outliers and essential/inessential states of the Markov chain, which allows us to detect outliers by using random walks. We provide a theoretical analysis that justifies the correctness of our method under geometric and connectivity assumptions. Experimental results on image databases demonstrate its superiority with respect to state-of-the-art sparse and low-rank outlier detection methods.