HSG-12M: A Large-Scale Spatial Multigraph Dataset

Existing graph benchmarks assume non-spatial, simple edges, collapsing physically distinct paths into a single link. We introduce HSG-12M, the first large-scale dataset of $\textbf{spatial multigraphs}-$graphs embedded in a metric space where multiple geometrically distinct trajectories between two nodes are retained as separate edges. HSG-12M contains 11.6 million static and 5.1 million dynamic $\textit{Hamiltonian spectral graphs}$ across 1401 characteristic-polynomial classes, derived from 177 TB of spectral potential data. Each graph encodes the full geometry of a 1-D crystal's energy spectrum on the complex plane, producing diverse, physics-grounded topologies that transcend conventional node-coordinate datasets. To enable future extensions, we release $\texttt{Poly2Graph}$: a high-performance, open-source pipeline that maps arbitrary 1-D crystal Hamiltonians to spectral graphs. Benchmarks with popular GNNs expose new challenges in learning from multi-edge geometry at scale. Beyond its practical utility, we show that spectral graphs serve as universal topological fingerprints of polynomials, vectors, and matrices, forging a new algebra-to-graph link. HSG-12M lays the groundwork for geometry-aware graph learning and new opportunities of data-driven scientific discovery in condensed matter physics and beyond.

Composing Music with Grammar Argumented Neural Networks and Note-Level Encoding

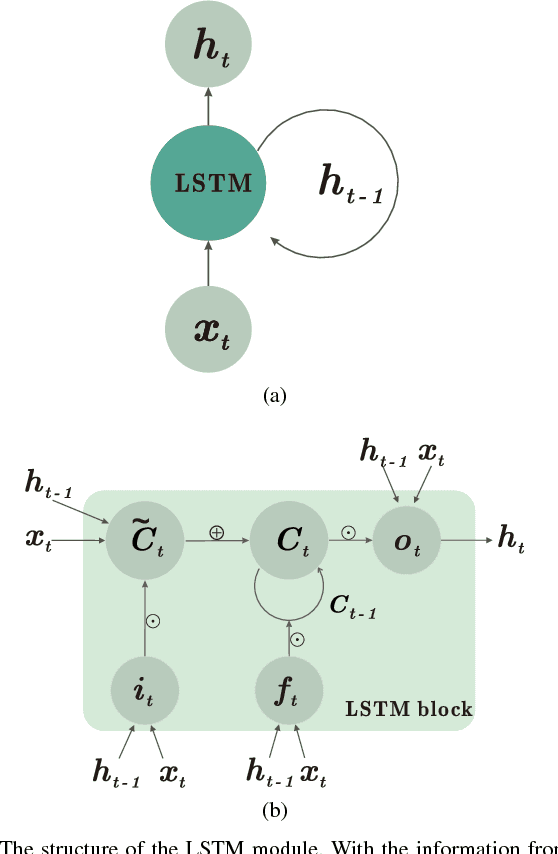
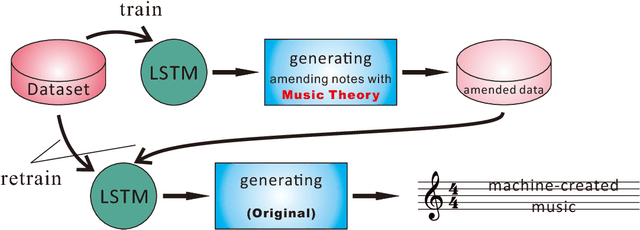
Creating aesthetically pleasing pieces of art, including music, has been a long-term goal for artificial intelligence research. Despite recent successes of long-short term memory (LSTM) recurrent neural networks (RNNs) in sequential learning, LSTM neural networks have not, by themselves, been able to generate natural-sounding music conforming to music theory. To transcend this inadequacy, we put forward a novel method for music composition that combines the LSTM with Grammars motivated by music theory. The main tenets of music theory are encoded as grammar argumented (GA) filters on the training data, such that the machine can be trained to generate music inheriting the naturalness of human-composed pieces from the original dataset while adhering to the rules of music theory. Unlike previous approaches, pitches and durations are encoded as one semantic entity, which we refer to as note-level encoding. This allows easy implementation of music theory grammars, as well as closer emulation of the thinking pattern of a musician. Although the GA rules are applied to the training data and never directly to the LSTM music generation, our machine still composes music that possess high incidences of diatonic scale notes, small pitch intervals and chords, in deference to music theory.