Robust and Consistent Ski Rental with Distributional Advice

The ski rental problem is a canonical model for online decision-making under uncertainty, capturing the fundamental trade-off between repeated rental costs and a one-time purchase. While classical algorithms focus on worst-case competitive ratios and recent "learning-augmented" methods leverage point-estimate predictions, neither approach fully exploits the richness of full distributional predictions while maintaining rigorous robustness guarantees. We address this gap by establishing a systematic framework that integrates distributional advice of unknown quality into both deterministic and randomized algorithms. For the deterministic setting, we formalize the problem under perfect distributional prediction and derive an efficient algorithm to compute the optimal threshold-buy day. We provide a rigorous performance analysis, identifying sufficient conditions on the predicted distribution under which the expected competitive ratio (ECR) matches the classic optimal randomized bound. To handle imperfect predictions, we propose the Clamp Policy, which restricts the buying threshold to a safe range controlled by a tunable parameter. We show that this policy is both robust, maintaining good performance even with large prediction errors, and consistent, approaching the optimal performance as predictions become accurate. For the randomized setting, we characterize the stopping distribution via a Water-Filling Algorithm, which optimizes expected cost while strictly satisfying robustness constraints. Experimental results across diverse distributions (Gaussian, geometric, and bi-modal) demonstrate that our framework improves consistency significantly over existing point-prediction baselines while maintaining comparable robustness.

Finding Differentially Private Second Order Stationary Points in Stochastic Minimax Optimization

We provide the first study of the problem of finding differentially private (DP) second-order stationary points (SOSP) in stochastic (non-convex) minimax optimization. Existing literature either focuses only on first-order stationary points for minimax problems or on SOSP for classical stochastic minimization problems. This work provides, for the first time, a unified and detailed treatment of both empirical and population risks. Specifically, we propose a purely first-order method that combines a nested gradient descent--ascent scheme with SPIDER-style variance reduction and Gaussian perturbations to ensure privacy. A key technical device is a block-wise ($q$-period) analysis that controls the accumulation of stochastic variance and privacy noise without summing over the full iteration horizon, yielding a unified treatment of both empirical-risk and population formulations. Under standard smoothness, Hessian-Lipschitzness, and strong concavity assumptions, we establish high-probability guarantees for reaching an $(α,\sqrt{ρ_Φα})$-approximate second-order stationary point with $α= \mathcal{O}( (\frac{\sqrt{d}}{n\varepsilon})^{2/3})$ for empirical risk objectives and $\mathcal{O}(\frac{1}{n^{1/3}} + (\frac{\sqrt{d}}{n\varepsilon})^{1/2})$ for population objectives, matching the best known rates for private first-order stationarity.

Learning-Augmented Ski Rental with Discrete Distributions: A Bayesian Approach

We revisit the classic ski rental problem through the lens of Bayesian decision-making and machine-learned predictions. While traditional algorithms minimize worst-case cost without assumptions, and recent learning-augmented approaches leverage noisy forecasts with robustness guarantees, our work unifies these perspectives. We propose a discrete Bayesian framework that maintains exact posterior distributions over the time horizon, enabling principled uncertainty quantification and seamless incorporation of expert priors. Our algorithm achieves prior-dependent competitive guarantees and gracefully interpolates between worst-case and fully-informed settings. Our extensive experimental evaluation demonstrates superior empirical performance across diverse scenarios, achieving near-optimal results under accurate priors while maintaining robust worst-case guarantees. This framework naturally extends to incorporate multiple predictions, non-uniform priors, and contextual information, highlighting the practical advantages of Bayesian reasoning in online decision problems with imperfect predictions.

Learning Augmented Graph $k$-Clustering

Clustering is a fundamental task in unsupervised learning. Previous research has focused on learning-augmented $k$-means in Euclidean metrics, limiting its applicability to complex data representations. In this paper, we generalize learning-augmented $k$-clustering to operate on general metrics, enabling its application to graph-structured and non-Euclidean domains. Our framework also relaxes restrictive cluster size constraints, providing greater flexibility for datasets with imbalanced or unknown cluster distributions. Furthermore, we extend the hardness of query complexity to general metrics: under the Exponential Time Hypothesis (ETH), we show that any polynomial-time algorithm must perform approximately $\Omega(k / \alpha)$ queries to achieve a $(1 + \alpha)$-approximation. These contributions strengthen both the theoretical foundations and practical applicability of learning-augmented clustering, bridging gaps between traditional methods and real-world challenges.

A Simple Analysis of Discretization Error in Diffusion Models

Diffusion models, formulated as discretizations of stochastic differential equations (SDEs), achieve state-of-the-art generative performance. However, existing analyses of their discretization error often rely on complex probabilistic tools. In this work, we present a simplified theoretical framework for analyzing the Euler--Maruyama discretization of variance-preserving SDEs (VP-SDEs) in Denoising Diffusion Probabilistic Models (DDPMs), where $ T $ denotes the number of denoising steps in the diffusion process. Our approach leverages Gr\"onwall's inequality to derive a convergence rate of $ \mathcal{O}(1/T^{1/2}) $ under Lipschitz assumptions, significantly streamlining prior proofs. Furthermore, we demonstrate that the Gaussian noise in the discretization can be replaced by a discrete random variable (e.g., Rademacher or uniform noise) without sacrificing convergence guarantees-an insight with practical implications for efficient sampling. Experiments validate our theory, showing that (1) the error scales as predicted, (2) discrete noise achieves comparable sample quality to Gaussian noise, and (3) incorrect noise scaling degrades performance. By unifying simplified analysis and discrete noise substitution, our work bridges theoretical rigor with practical efficiency in diffusion-based generative modeling.

Noise is All You Need: Private Second-Order Convergence of Noisy SGD

Private optimization is a topic of major interest in machine learning, with differentially private stochastic gradient descent (DP-SGD) playing a key role in both theory and practice. Furthermore, DP-SGD is known to be a powerful tool in contexts beyond privacy, including robustness, machine unlearning, etc. Existing analyses of DP-SGD either make relatively strong assumptions (e.g., Lipschitz continuity of the loss function, or even convexity) or prove only first-order convergence (and thus might end at a saddle point in the non-convex setting). At the same time, there has been progress in proving second-order convergence of the non-private version of ``noisy SGD'', as well as progress in designing algorithms that are more complex than DP-SGD and do guarantee second-order convergence. We revisit DP-SGD and show that ``noise is all you need'': the noise necessary for privacy already implies second-order convergence under the standard smoothness assumptions, even for non-Lipschitz loss functions. Hence, we get second-order convergence essentially for free: DP-SGD, the workhorse of modern private optimization, under minimal assumptions can be used to find a second-order stationary point.

Faster Algorithms for Generalized Mean Densest Subgraph Problem

The densest subgraph of a large graph usually refers to some subgraph with the highest average degree, which has been extended to the family of $p$-means dense subgraph objectives by~\citet{veldt2021generalized}. The $p$-mean densest subgraph problem seeks a subgraph with the highest average $p$-th-power degree, whereas the standard densest subgraph problem seeks a subgraph with a simple highest average degree. It was shown that the standard peeling algorithm can perform arbitrarily poorly on generalized objective when $p>1$ but uncertain when $0<p<1$. In this paper, we are the first to show that a standard peeling algorithm can still yield $2^{1/p}$-approximation for the case $0<p < 1$. (Veldt 2021) proposed a new generalized peeling algorithm (GENPEEL), which for $p \geq 1$ has an approximation guarantee ratio $(p+1)^{1/p}$, and time complexity $O(mn)$, where $m$ and $n$ denote the number of edges and nodes in graph respectively. In terms of algorithmic contributions, we propose a new and faster generalized peeling algorithm (called GENPEEL++ in this paper), which for $p \in [1, +\infty)$ has an approximation guarantee ratio $(2(p+1))^{1/p}$, and time complexity $O(m(\log n))$, where $m$ and $n$ denote the number of edges and nodes in graph, respectively. This approximation ratio converges to 1 as $p \rightarrow \infty$.

$k$-Median Clustering via Metric Embedding: Towards Better Initialization with Differential Privacy

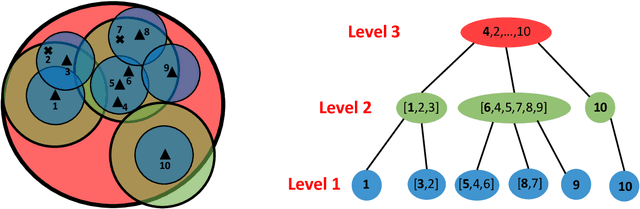
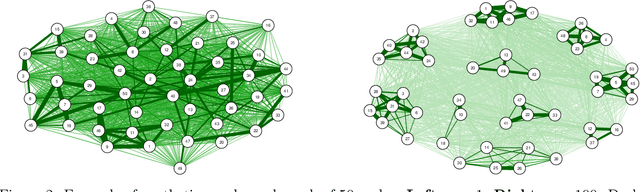
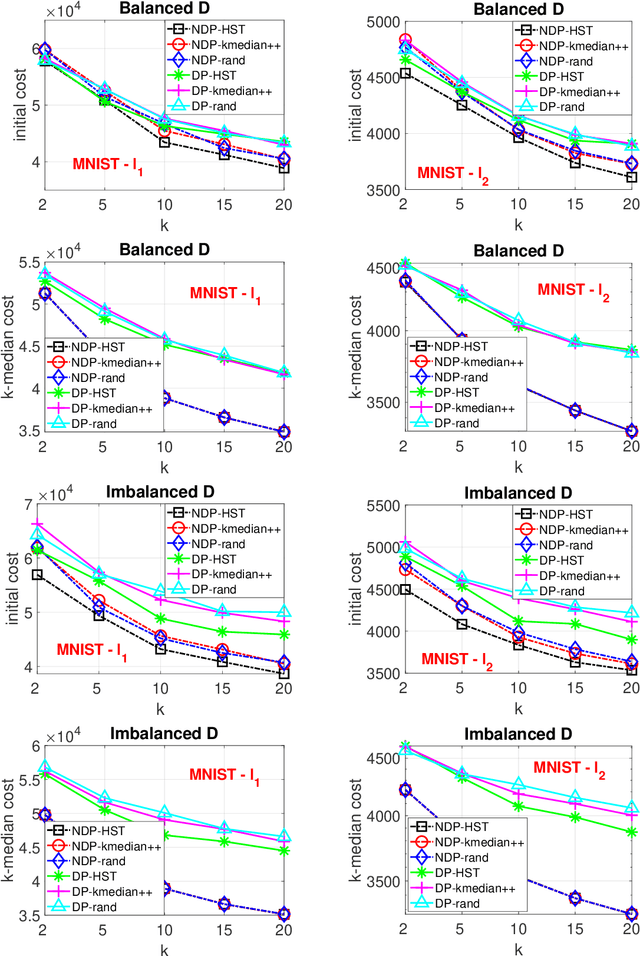
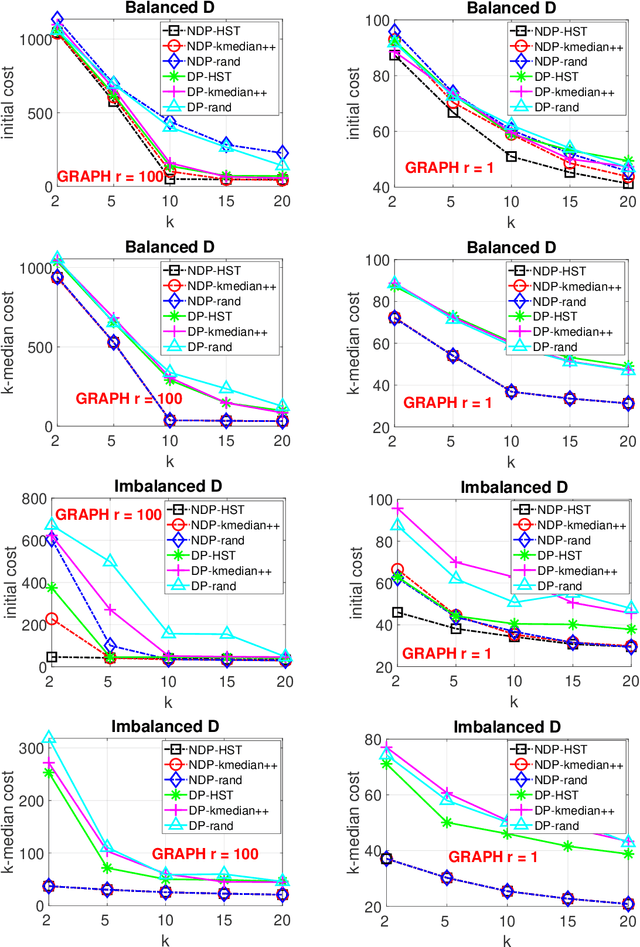
When designing clustering algorithms, the choice of initial centers is crucial for the quality of the learned clusters. In this paper, we develop a new initialization scheme, called HST initialization, for the $k$-median problem in the general metric space (e.g., discrete space induced by graphs), based on the construction of metric embedding tree structure of the data. From the tree, we propose a novel and efficient search algorithm, for good initial centers that can be used subsequently for the local search algorithm. Our proposed HST initialization can produce initial centers achieving lower errors than those from another popular initialization method, $k$-median++, with comparable efficiency. The HST initialization can also be extended to the setting of differential privacy (DP) to generate private initial centers. We show that the error from applying DP local search followed by our private HST initialization improves previous results on the approximation error, and approaches the lower bound within a small factor. Experiments justify the theory and demonstrate the effectiveness of our proposed method. Our approach can also be extended to the $k$-means problem.

Near-Optimal Correlation Clustering with Privacy

Correlation clustering is a central problem in unsupervised learning, with applications spanning community detection, duplicate detection, automated labelling and many more. In the correlation clustering problem one receives as input a set of nodes and for each node a list of co-clustering preferences, and the goal is to output a clustering that minimizes the disagreement with the specified nodes' preferences. In this paper, we introduce a simple and computationally efficient algorithm for the correlation clustering problem with provable privacy guarantees. Our approximation guarantees are stronger than those shown in prior work and are optimal up to logarithmic factors.