Binary Search with Distributional Predictions

Algorithms with (machine-learned) predictions is a powerful framework for combining traditional worst-case algorithms with modern machine learning. However, the vast majority of work in this space assumes that the prediction itself is non-probabilistic, even if it is generated by some stochastic process (such as a machine learning system). This is a poor fit for modern ML, particularly modern neural networks, which naturally generate a distribution. We initiate the study of algorithms with distributional predictions, where the prediction itself is a distribution. We focus on one of the simplest yet fundamental settings: binary search (or searching a sorted array). This setting has one of the simplest algorithms with a point prediction, but what happens if the prediction is a distribution? We show that this is a richer setting: there are simple distributions where using the classical prediction-based algorithm with any single prediction does poorly. Motivated by this, as our main result, we give an algorithm with query complexity $O(H(p) + \log \eta)$, where $H(p)$ is the entropy of the true distribution $p$ and $\eta$ is the earth mover's distance between $p$ and the predicted distribution $\hat p$. This also yields the first distributionally-robust algorithm for the classical problem of computing an optimal binary search tree given a distribution over target keys. We complement this with a lower bound showing that this query complexity is essentially optimal (up to constants), and experiments validating the practical usefulness of our algorithm.

Noise is All You Need: Private Second-Order Convergence of Noisy SGD

Private optimization is a topic of major interest in machine learning, with differentially private stochastic gradient descent (DP-SGD) playing a key role in both theory and practice. Furthermore, DP-SGD is known to be a powerful tool in contexts beyond privacy, including robustness, machine unlearning, etc. Existing analyses of DP-SGD either make relatively strong assumptions (e.g., Lipschitz continuity of the loss function, or even convexity) or prove only first-order convergence (and thus might end at a saddle point in the non-convex setting). At the same time, there has been progress in proving second-order convergence of the non-private version of ``noisy SGD'', as well as progress in designing algorithms that are more complex than DP-SGD and do guarantee second-order convergence. We revisit DP-SGD and show that ``noise is all you need'': the noise necessary for privacy already implies second-order convergence under the standard smoothness assumptions, even for non-Lipschitz loss functions. Hence, we get second-order convergence essentially for free: DP-SGD, the workhorse of modern private optimization, under minimal assumptions can be used to find a second-order stationary point.

Controlling Epidemic Spread using Probabilistic Diffusion Models on Networks

The spread of an epidemic is often modeled by an SIR random process on a social network graph. The MinINF problem for optimal social distancing involves minimizing the expected number of infections, when we are allowed to break at most $B$ edges; similarly the MinINFNode problem involves removing at most $B$ vertices. These are fundamental problems in epidemiology and network science. While a number of heuristics have been considered, the complexity of these problems remains generally open. In this paper, we present two bicriteria approximation algorithms for MinINF, which give the first non-trivial approximations for this problem. The first is based on the cut sparsification result of Karger \cite{karger:mathor99}, and works when the transmission probabilities are not too small. The second is a Sample Average Approximation (SAA) based algorithm, which we analyze for the Chung-Lu random graph model. We also extend some of our results to tackle the MinINFNode problem.

Faster Matchings via Learned Duals

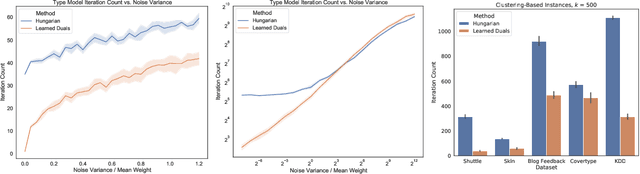
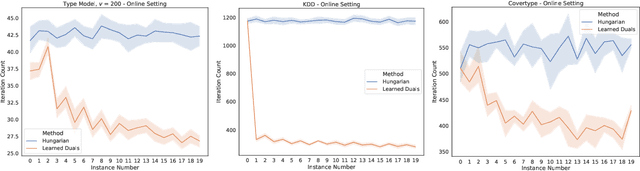
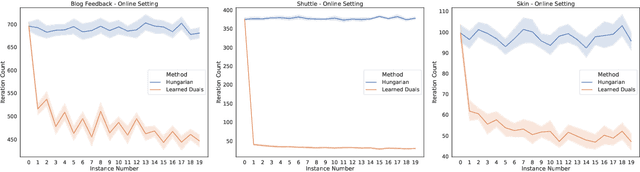
A recent line of research investigates how algorithms can be augmented with machine-learned predictions to overcome worst case lower bounds. This area has revealed interesting algorithmic insights into problems, with particular success in the design of competitive online algorithms. However, the question of improving algorithm running times with predictions has largely been unexplored. We take a first step in this direction by combining the idea of machine-learned predictions with the idea of "warm-starting" primal-dual algorithms. We consider one of the most important primitives in combinatorial optimization: weighted bipartite matching and its generalization to $b$-matching. We identify three key challenges when using learned dual variables in a primal-dual algorithm. First, predicted duals may be infeasible, so we give an algorithm that efficiently maps predicted infeasible duals to nearby feasible solutions. Second, once the duals are feasible, they may not be optimal, so we show that they can be used to quickly find an optimal solution. Finally, such predictions are useful only if they can be learned, so we show that the problem of learning duals for matching has low sample complexity. We validate our theoretical findings through experiments on both real and synthetic data. As a result we give a rigorous, practical, and empirically effective method to compute bipartite matchings.

Fair Disaster Containment via Graph-Cut Problems

Graph cut problems form a fundamental problem type in combinatorial optimization, and are a central object of study in both theory and practice. In addition, the study of fairness in Algorithmic Design and Machine Learning has recently received significant attention, with many different notions proposed and analyzed in a variety of contexts. In this paper we initiate the study of fairness for graph cut problems by giving the first fair definitions for them, and subsequently we demonstrate appropriate algorithmic techniques that yield a rigorous theoretical analysis. Specifically, we incorporate two different definitions of fairness, namely demographic and probabilistic individual fairness, in a particular cut problem modeling disaster containment scenarios. Our results include a variety of approximation algorithms with provable theoretical guarantees.

Policy Regret in Repeated Games

The notion of \emph{policy regret} in online learning is a well defined? performance measure for the common scenario of adaptive adversaries, which more traditional quantities such as external regret do not take into account. We revisit the notion of policy regret and first show that there are online learning settings in which policy regret and external regret are incompatible: any sequence of play that achieves a favorable regret with respect to one definition must do poorly with respect to the other. We then focus on the game-theoretic setting where the adversary is a self-interested agent. In that setting, we show that external regret and policy regret are not in conflict and, in fact, that a wide class of algorithms can ensure a favorable regret with respect to both definitions, so long as the adversary is also using such an algorithm. We also show that the sequence of play of no-policy regret algorithms converges to a \emph{policy equilibrium}, a new notion of equilibrium that we introduce. Relating this back to external regret, we show that coarse correlated equilibria, which no-external regret players converge to, are a strict subset of policy equilibria. Thus, in game-theoretic settings, every sequence of play with no external regret also admits no policy regret, but the converse does not hold.