Decision Forests Induce Characteristic Kernels

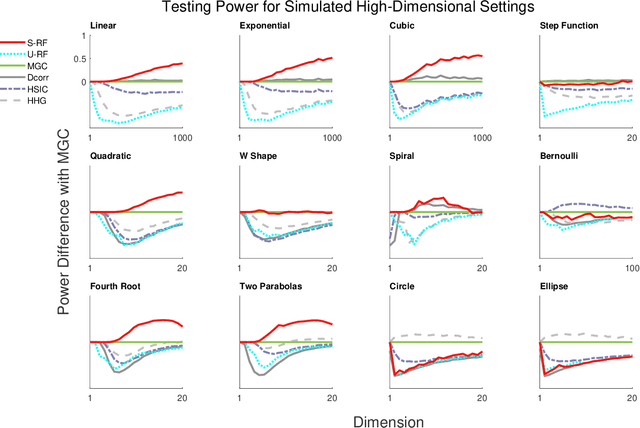
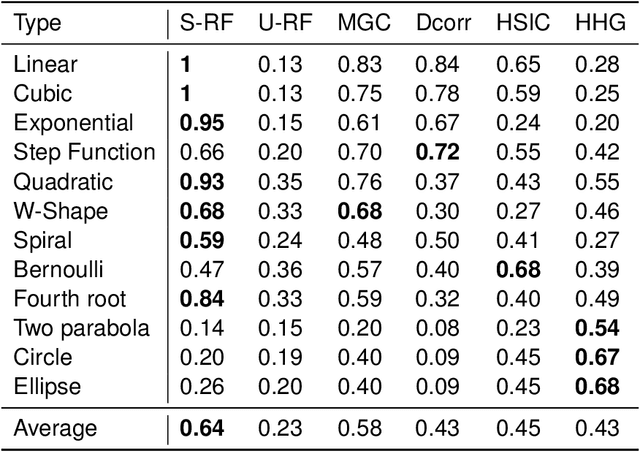
Decision forests are popular tools for classification and regression. These forests naturally produce proximity matrices measuring how often each pair of observations lies in the same leaf node. Recently it has been demonstrated that these proximity matrices can be thought of as kernels, connecting the decision forest literature to the extensive kernel machine literature. While other kernels are known to have strong theoretical properties, such as being characteristic kernels, no similar result is available for any decision forest based kernel. We show that a decision forest induced proximity can be made into a characteristic kernel, which can be used within an independence test to obtain a universally consistent test. We therefore empirically evaluate this kernel on a suite of 12 high-dimensional independence test settings: the decision forest induced kernel is shown to typically achieve substantially higher power than other methods.

Random Projection Forests

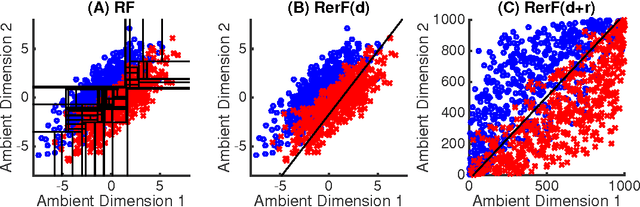
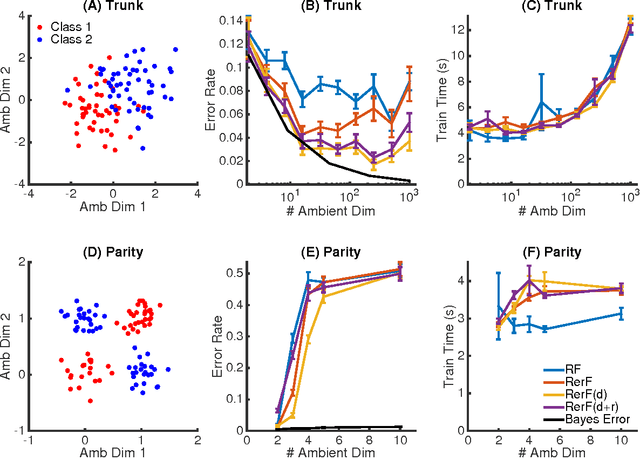
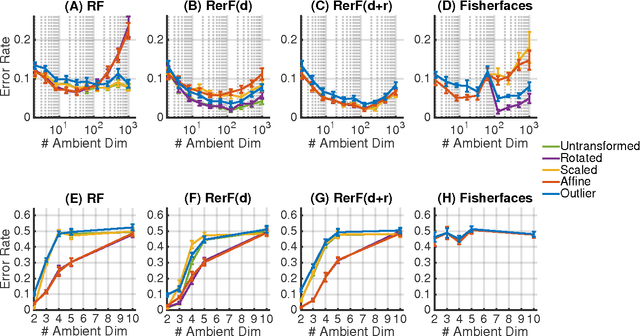
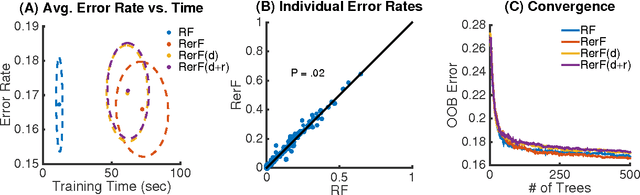
Ensemble methods---particularly those based on decision trees---have recently demonstrated superior performance in a variety of machine learning settings. We introduce a generalization of many existing decision tree methods called "Random Projection Forests" (RPF), which is any decision forest that uses (possibly data dependent and random) linear projections. Using this framework, we introduce a special case, called "Lumberjack", using very sparse random projections, that is, linear combinations of a small subset of features. Lumberjack obtains statistically significantly improved accuracy over Random Forests, Gradient Boosted Trees, and other approaches on a standard benchmark suites for classification with varying dimension, sample size, and number of classes. To illustrate how, why, and when Lumberjack outperforms other methods, we conduct extensive simulated experiments, in vectors, images, and nonlinear manifolds. Lumberjack typically yields improved performance over existing decision trees ensembles, while mitigating computational efficiency and scalability, and maintaining interpretability. Lumberjack can easily be incorporated into other ensemble methods such as boosting to obtain potentially similar gains.

From Distance Correlation to Multiscale Graph Correlation

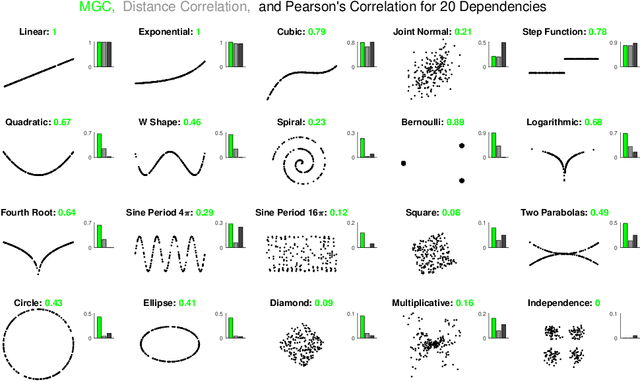
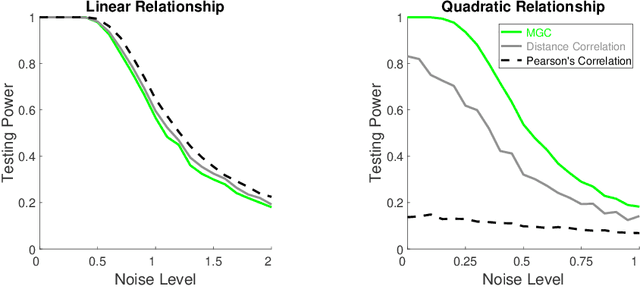
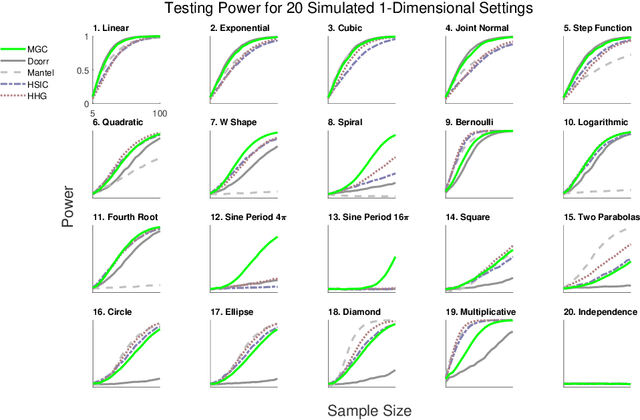
Understanding and developing a correlation measure that can detect general dependencies is not only imperative to statistics and machine learning, but also crucial to general scientific discovery in the big data age. In this paper, we establish a new framework that generalizes distance correlation --- a correlation measure that was recently proposed and shown to be universally consistent for dependence testing against all joint distributions of finite moments --- to the Multiscale Graph Correlation (MGC). By utilizing the characteristic functions and incorporating the nearest neighbor machinery, we formalize the population version of local distance correlations, define the optimal scale in a given dependency, and name the optimal local correlation as MGC. The new theoretical framework motivates a theoretically sound Sample MGC and allows a number of desirable properties to be proved, including the universal consistency, convergence and almost unbiasedness of the sample version. The advantages of MGC are illustrated via a comprehensive set of simulations with linear, nonlinear, univariate, multivariate, and noisy dependencies, where it loses almost no power in monotone dependencies while achieving better performance in general dependencies, compared to distance correlation and other popular methods.

Discovering and Deciphering Relationships Across Disparate Data Modalities

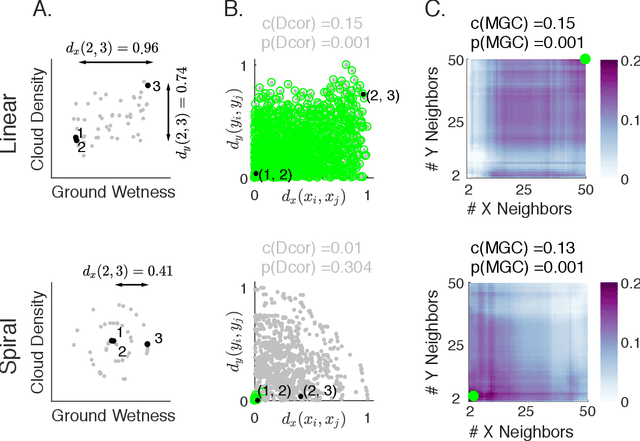
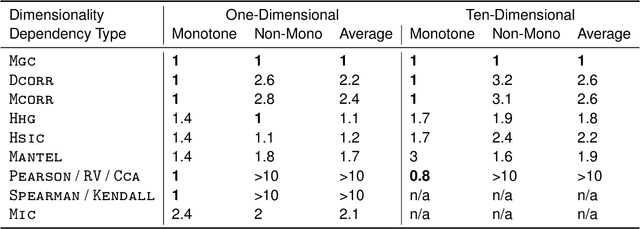
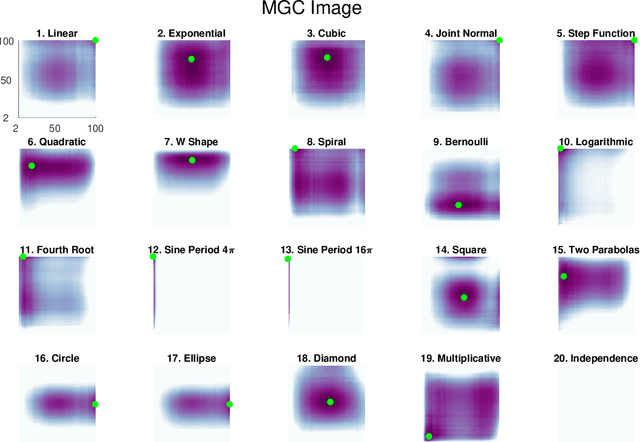
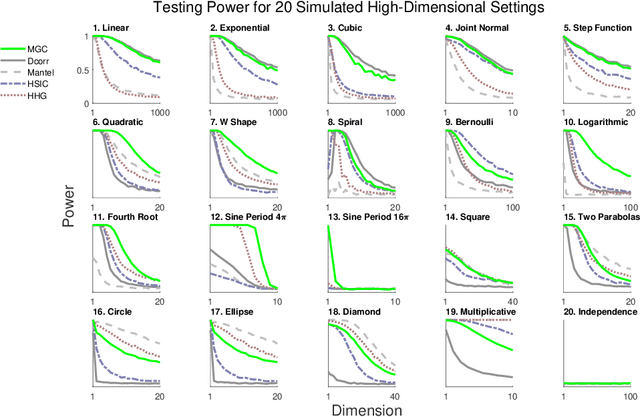
Understanding the relationships between different properties of data, such as whether a connectome or genome has information about disease status, is becoming increasingly important in modern biological datasets. While existing approaches can test whether two properties are related, they often require unfeasibly large sample sizes in real data scenarios, and do not provide any insight into how or why the procedure reached its decision. Our approach, "Multiscale Graph Correlation" (MGC), is a dependence test that juxtaposes previously disparate data science techniques, including k-nearest neighbors, kernel methods (such as support vector machines), and multiscale analysis (such as wavelets). Other methods typically require double or triple the number samples to achieve the same statistical power as MGC in a benchmark suite including high-dimensional and nonlinear relationships - spanning polynomial (linear, quadratic, cubic), trigonometric (sinusoidal, circular, ellipsoidal, spiral), geometric (square, diamond, W-shape), and other functions, with dimensionality ranging from 1 to 1000. Moreover, MGC uniquely provides a simple and elegant characterization of the potentially complex latent geometry underlying the relationship, providing insight while maintaining computational efficiency. In several real data applications, including brain imaging and cancer genetics, MGC is the only method that can both detect the presence of a dependency and provide specific guidance for the next experiment and/or analysis to conduct.

The Exact Equivalence of Distance and Kernel Methods for Hypothesis Testing

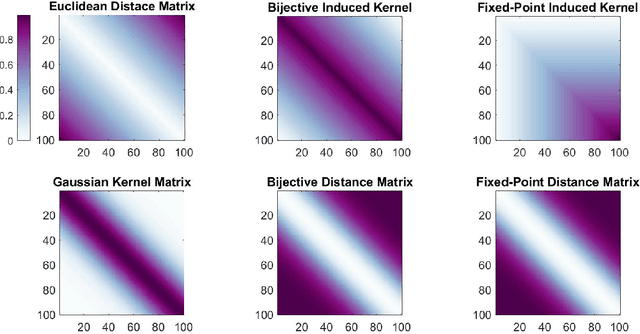
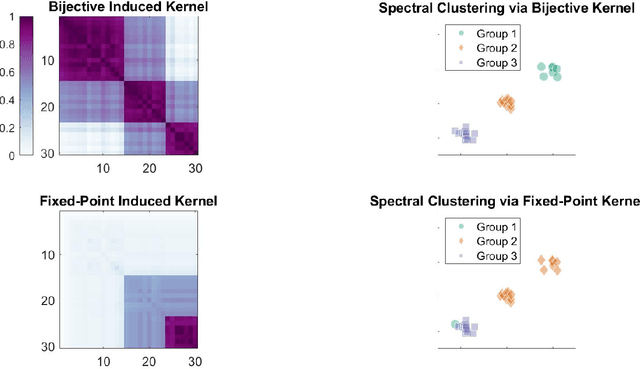
Distance-based methods, also called "energy statistics", are leading methods for two-sample and independence tests from the statistics community. Kernel methods, developed from "kernel mean embeddings", are leading methods for two-sample and independence tests from the machine learning community. Previous works demonstrated the equivalence of distance and kernel methods only at the population level, for each kind of test, requiring an embedding theory of kernels. We propose a simple, bijective transformation between semimetrics and nondegenerate kernels. We prove that for finite samples, two-sample tests are special cases of independence tests, and the distance-based statistic is equivalent to the kernel-based statistic, including the biased, unbiased, and normalized versions. In other words, upon setting the kernel or metric to be bijective of each other, running any of the four algorithms will yield the exact same answer up to numerical precision. This deepens and unifies our understanding of interpoint comparison based methods.

Sparse Representation Classification Beyond L1 Minimization and the Subspace Assumption

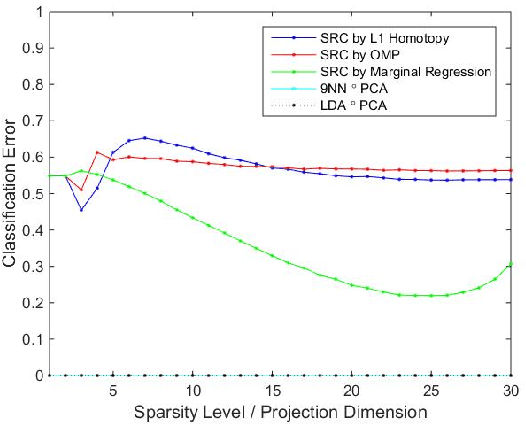
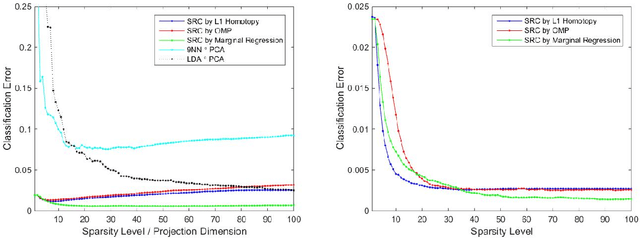
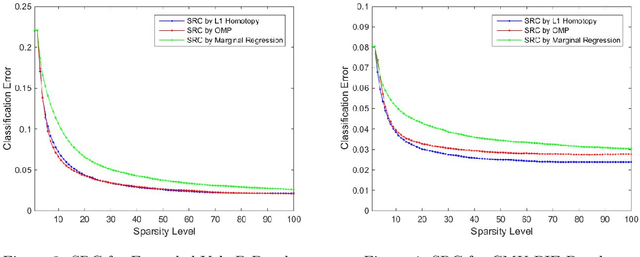
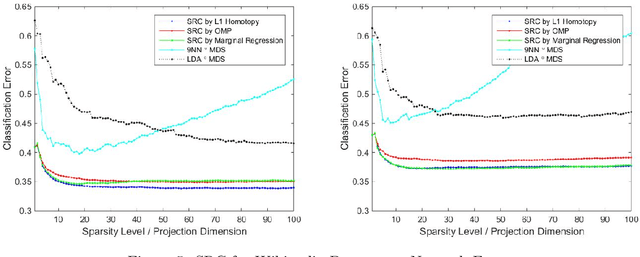
The sparse representation classifier (SRC) has been utilized in various classification problems, which makes use of L1 minimization and is shown to work well for image recognition problems that satisfy a subspace assumption. In this paper we propose a new implementation of SRC via screening, establish its equivalence to the original SRC under regularity conditions, and prove its classification consistency under a latent subspace model. The results are demonstrated via simulations and real data experiments, where the new algorithm achieves comparable numerical performance but significantly faster.

Manifold Matching using Shortest-Path Distance and Joint Neighborhood Selection

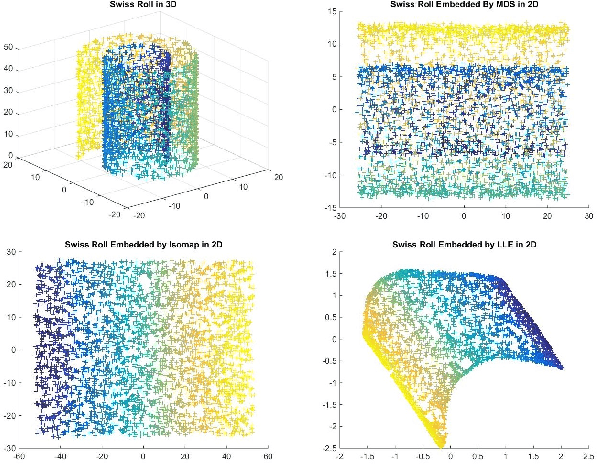
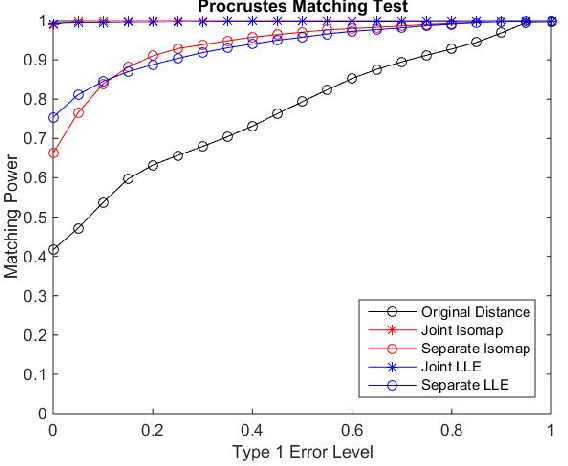
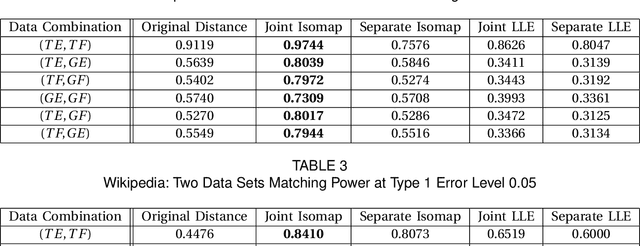
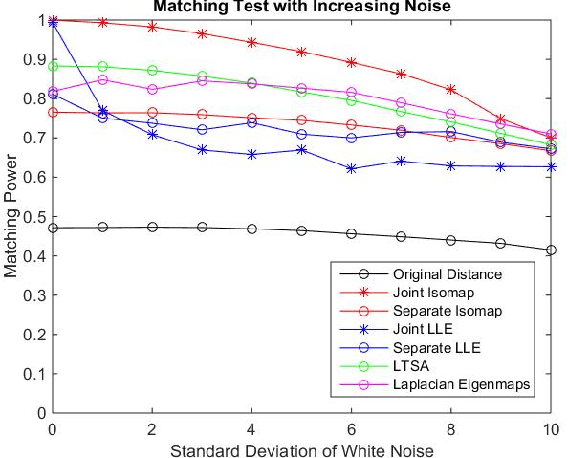
Matching datasets of multiple modalities has become an important task in data analysis. Existing methods often rely on the embedding and transformation of each single modality without utilizing any correspondence information, which often results in sub-optimal matching performance. In this paper, we propose a nonlinear manifold matching algorithm using shortest-path distance and joint neighborhood selection. Specifically, a joint nearest-neighbor graph is built for all modalities. Then the shortest-path distance within each modality is calculated from the joint neighborhood graph, followed by embedding into and matching in a common low-dimensional Euclidean space. Compared to existing algorithms, our approach exhibits superior performance for matching disparate datasets of multiple modalities.

Robust Vertex Classification

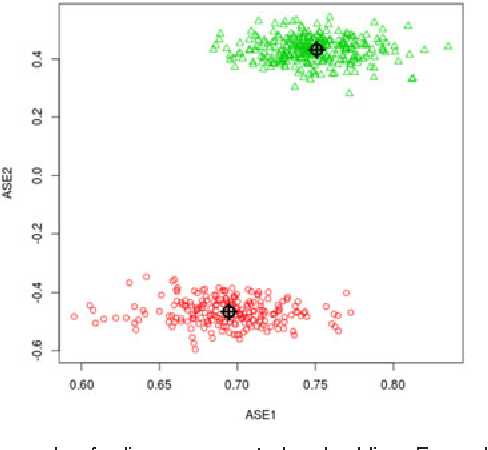
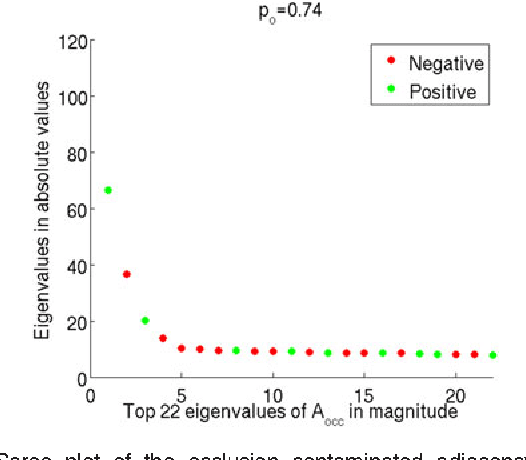
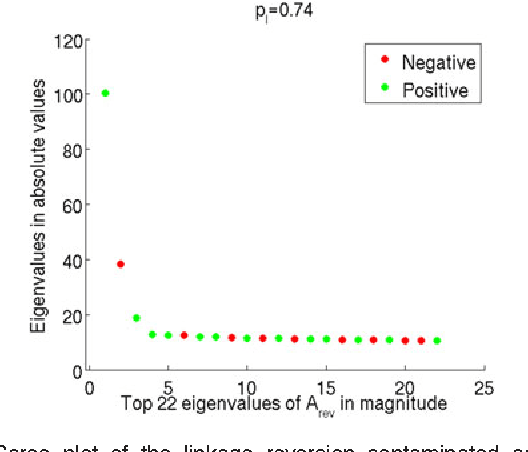
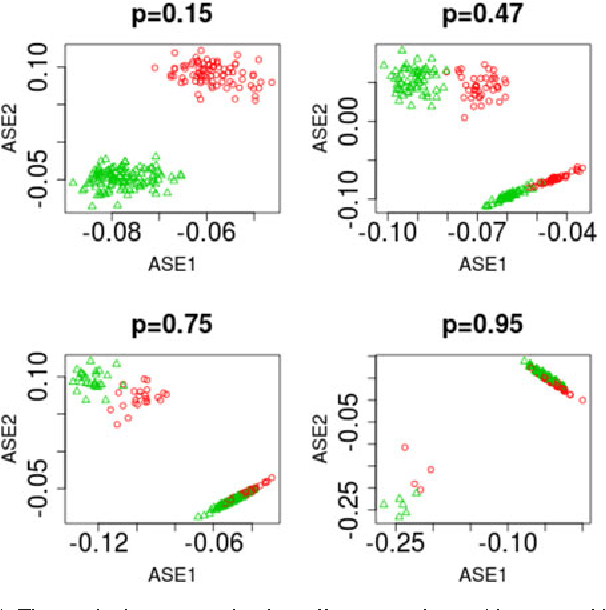
For random graphs distributed according to stochastic blockmodels, a special case of latent position graphs, adjacency spectral embedding followed by appropriate vertex classification is asymptotically Bayes optimal; but this approach requires knowledge of and critically depends on the model dimension. In this paper, we propose a sparse representation vertex classifier which does not require information about the model dimension. This classifier represents a test vertex as a sparse combination of the vertices in the training set and uses the recovered coefficients to classify the test vertex. We prove consistency of our proposed classifier for stochastic blockmodels, and demonstrate that the sparse representation classifier can predict vertex labels with higher accuracy than adjacency spectral embedding approaches via both simulation studies and real data experiments. Our results demonstrate the robustness and effectiveness of our proposed vertex classifier when the model dimension is unknown.

On the Incommensurability Phenomenon

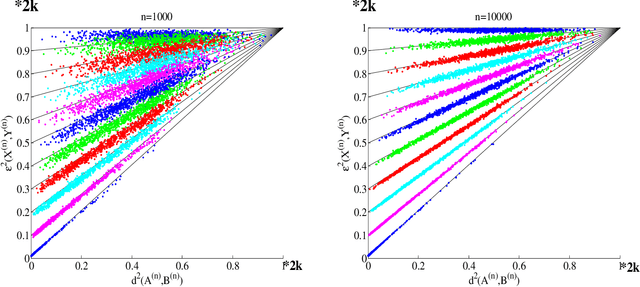
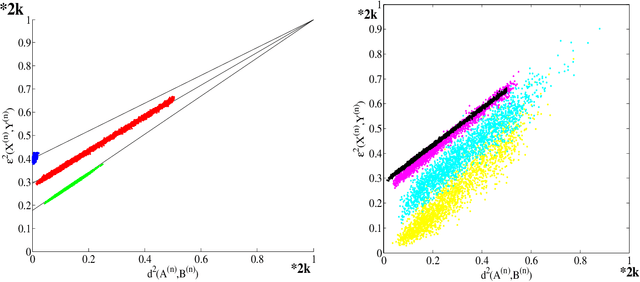
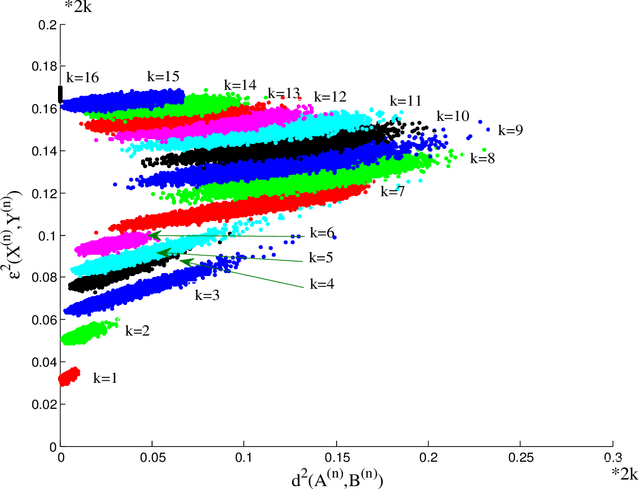
Suppose that two large, multi-dimensional data sets are each noisy measurements of the same underlying random process, and principle components analysis is performed separately on the data sets to reduce their dimensionality. In some circumstances it may happen that the two lower-dimensional data sets have an inordinately large Procrustean fitting-error between them. The purpose of this manuscript is to quantify this "incommensurability phenomenon." In particular, under specified conditions, the square Procrustean fitting-error of the two normalized lower-dimensional data sets is (asymptotically) a convex combination (via a correlation parameter) of the Hausdorff distance between the projection subspaces and the maximum possible value of the square Procrustean fitting-error for normalized data. We show how this gives rise to the incommensurability phenomenon, and we employ illustrative simulations as well as a real data experiment to explore how the incommensurability phenomenon may have an appreciable impact.

Generalized Canonical Correlation Analysis for Classification

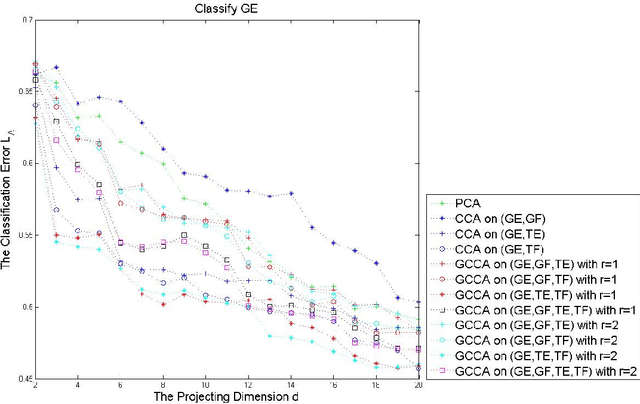
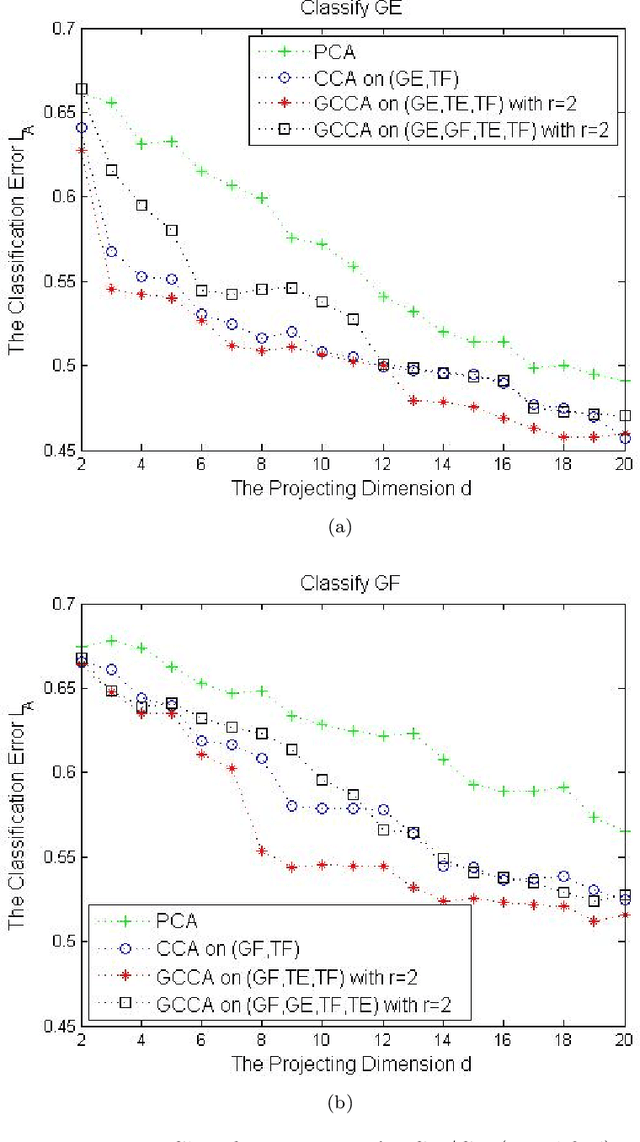
For multiple multivariate data sets, we derive conditions under which Generalized Canonical Correlation Analysis (GCCA) improves classification performance of the projected datasets, compared to standard Canonical Correlation Analysis (CCA) using only two data sets. We illustrate our theoretical results with simulations and a real data experiment.