Preordering: A hybrid of correlation clustering and partial ordering

We discuss the preordering problem, a joint relaxation of the correlation clustering problem and the partial ordering problem. We show that preordering remains NP-hard even for values in $\{-1,0,1\}$. We introduce a linear-time $4$-approximation algorithm and a local search technique. For an integer linear program formulation, we establish a class of non-canonical facets of the associated preorder polytope. By solving a non-canonical linear program relaxation, we obtain non-trivial upper bounds on the objective value. We provide implementations of the algorithms we define, apply these to published social networks and compare the output and efficiency qualitatively and quantitatively.

Correlation Clustering of Organoid Images

In biological and medical research, scientists now routinely acquire microscopy images of hundreds of morphologically heterogeneous organoids and are then faced with the task of finding patterns in the image collection, i.e., subsets of organoids that appear similar and potentially represent the same morphological class. We adopt models and algorithms for correlating organoid images, i.e., for quantifying the similarity in appearance and geometry of the organoids they depict, and for clustering organoid images by consolidating conflicting correlations. For correlating organoid images, we adopt and compare two alternatives, a partial quadratic assignment problem and a twin network. For clustering organoid images, we employ the correlation clustering problem. Empirically, we learn the parameters of these models, infer a clustering of organoid images, and quantify the accuracy of the inferred clusters, with respect to a training set and a test set we contribute of state-of-the-art light microscopy images of organoids clustered manually by biologists.

Cut Facets and Cube Facets of Lifted Multicut Polytopes

The lifted multicut problem has diverse applications in the field of computer vision. Exact algorithms based on linear programming require an understanding of lifted multicut polytopes. Despite recent progress, two fundamental questions about these polytopes have remained open: Which lower cube inequalities define facets, and which cut inequalities define facets? In this article, we answer the first question by establishing conditions that are necessary, sufficient and efficiently decidable. Toward the second question, we show that deciding facet-definingness of cut inequalities is NP-hard. This completes the analysis of canonical facets of lifted multicut polytopes.

A 4-approximation algorithm for min max correlation clustering

We introduce a lower bounding technique for the min max correlation clustering problem and, based on this technique, a combinatorial 4-approximation algorithm for complete graphs. This improves upon the previous best known approximation guarantees of 5, using a linear program formulation (Kalhan et al., 2019), and 40, for a combinatorial algorithm (Davies et al., 2023). We extend this algorithm by a greedy joining heuristic and show empirically that it improves the state of the art in solution quality and runtime on several benchmark datasets.

A Graph Multi-separator Problem for Image Segmentation

We propose a novel abstraction of the image segmentation task in the form of a combinatorial optimization problem that we call the multi-separator problem. Feasible solutions indicate for every pixel whether it belongs to a segment or a segment separator, and indicate for pairs of pixels whether or not the pixels belong to the same segment. This is in contrast to the closely related lifted multicut problem where every pixel is associated to a segment and no pixel explicitly represents a separating structure. While the multi-separator problem is NP-hard, we identify two special cases for which it can be solved efficiently. Moreover, we define two local search algorithms for the general case and demonstrate their effectiveness in segmenting simulated volume images of foam cells and filaments.

Correlation Clustering of Bird Sounds

Bird sound classification is the task of relating any sound recording to those species of bird that can be heard in the recording. Here, we study bird sound clustering, the task of deciding for any pair of sound recordings whether the same species of bird can be heard in both. We address this problem by first learning, from a training set, probabilities of pairs of recordings being related in this way, and then inferring a maximally probable partition of a test set by correlation clustering. We address the following questions: How accurate is this clustering, compared to a classification of the test set? How do the clusters thus inferred relate to the clusters obtained by classification? How accurate is this clustering when applied to recordings of bird species not heard during training? How effective is this clustering in separating, from bird sounds, environmental noise not heard during training?

Partial Optimality in Cubic Correlation Clustering

The higher-order correlation clustering problem is an expressive model, and recently, local search heuristics have been proposed for several applications. Certifying optimality, however, is NP-hard and practically hampered already by the complexity of the problem statement. Here, we focus on establishing partial optimality conditions for the special case of complete graphs and cubic objective functions. In addition, we define and implement algorithms for testing these conditions and examine their effect numerically, on two datasets.

A Polyhedral Study of Lifted Multicuts

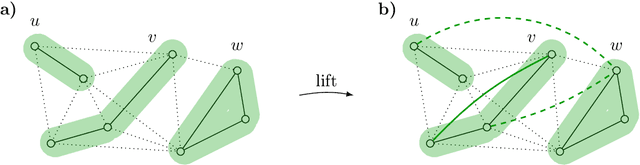
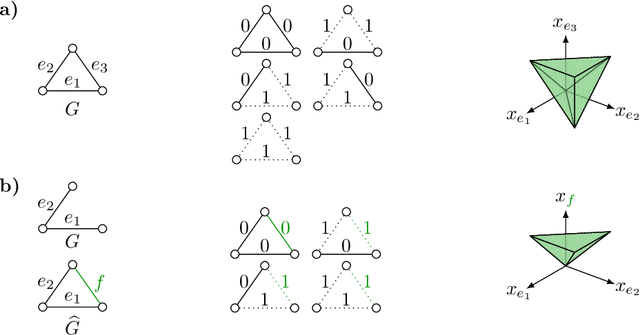
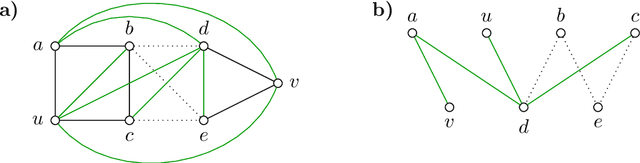
Fundamental to many applications in data analysis are the decompositions of a graph, i.e. partitions of the node set into component-inducing subsets. One way of encoding decompositions is by multicuts, the subsets of those edges that straddle distinct components. Recently, a lifting of multicuts from a graph $G = (V, E)$ to an augmented graph $\hat G = (V, E \cup F)$ has been proposed in the field of image analysis, with the goal of obtaining a more expressive characterization of graph decompositions in which it is made explicit also for pairs $F \subseteq \tbinom{V}{2} \setminus E$ of non-neighboring nodes whether these are in the same or distinct components. In this work, we study in detail the polytope in $\mathbb{R}^{E \cup F}$ whose vertices are precisely the characteristic vectors of multicuts of $\hat G$ lifted from $G$, connecting it, in particular, to the rich body of prior work on the clique partitioning and multilinear polytope.

Inapproximability of Minimizing a Pair of DNFs or Binary Decision Trees Defining a Partial Boolean Function

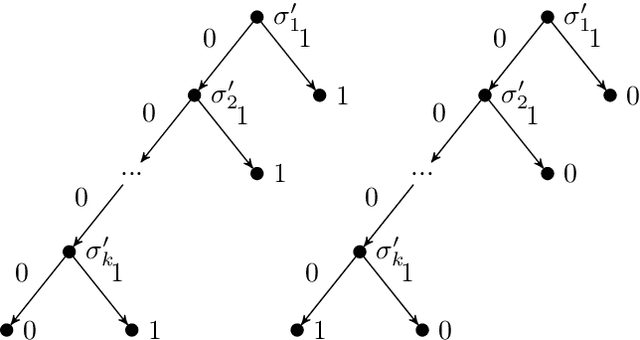
The desire to apply machine learning techniques in safety-critical environments has renewed interest in the learning of partial functions for distinguishing between positive, negative and unclear observations. We contribute to the understanding of the hardness of this problem. Specifically, we consider partial Boolean functions defined by a pair of Boolean functions $f, g \colon \{0,1\}^J \to \{0,1\}$ such that $f \cdot g = 0$ and such that $f$ and $g$ are defined by disjunctive normal forms or binary decision trees. We show: Minimizing the sum of the lengths or depths of these forms while separating disjoint sets $A \cup B = S \subseteq \{0,1\}^J$ such that $f(A) = \{1\}$ and $g(B) = \{1\}$ is inapproximable to within $(1 - \epsilon) \ln (|S|-1)$ for any $\epsilon > 0$, unless P=NP.

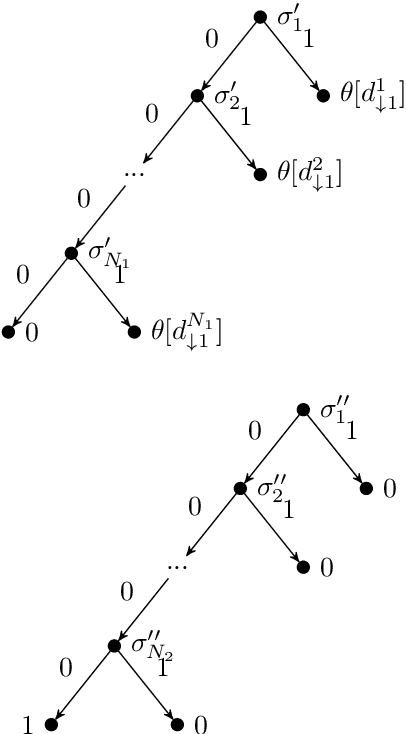
End-to-end Learning for Graph Decomposition

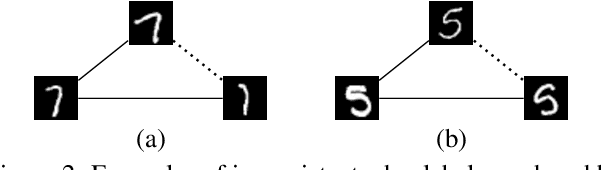
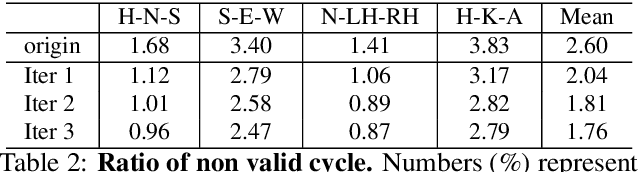
We propose a novel end-to-end trainable framework for the graph decomposition problem. The minimum cost multicut problem is first converted to an unconstrained binary cubic formulation where cycle consistency constraints are incorporated into the objective function. The new optimization problem can be viewed as a Conditional Random Field (CRF) in which the random variables are associated with the binary edge labels of the initial graph and the hard constraints are introduced in the CRF as high-order potentials. The parameters of a standard Neural Network and the fully differentiable CRF are optimized in an end-to-end manner. Furthermore, our method utilizes the cycle constraints as meta-supervisory signals during the learning of the deep feature representations by taking the dependencies between the output random variables into account. We present analyses of the end-to-end learned representations, showing the impact of the joint training, on the task of clustering images of MNIST. We also validate the effectiveness of our approach both for the feature learning and the final clustering on the challenging task of real-world multi-person pose estimation.