Jannik Irmai
Preordering: A hybrid of correlation clustering and partial ordering
Feb 20, 2025Abstract:We discuss the preordering problem, a joint relaxation of the correlation clustering problem and the partial ordering problem. We show that preordering remains NP-hard even for values in $\{-1,0,1\}$. We introduce a linear-time $4$-approximation algorithm and a local search technique. For an integer linear program formulation, we establish a class of non-canonical facets of the associated preorder polytope. By solving a non-canonical linear program relaxation, we obtain non-trivial upper bounds on the objective value. We provide implementations of the algorithms we define, apply these to published social networks and compare the output and efficiency qualitatively and quantitatively.
Cut Facets and Cube Facets of Lifted Multicut Polytopes
Feb 26, 2024Abstract:The lifted multicut problem has diverse applications in the field of computer vision. Exact algorithms based on linear programming require an understanding of lifted multicut polytopes. Despite recent progress, two fundamental questions about these polytopes have remained open: Which lower cube inequalities define facets, and which cut inequalities define facets? In this article, we answer the first question by establishing conditions that are necessary, sufficient and efficiently decidable. Toward the second question, we show that deciding facet-definingness of cut inequalities is NP-hard. This completes the analysis of canonical facets of lifted multicut polytopes.
A 4-approximation algorithm for min max correlation clustering
Oct 30, 2023Abstract:We introduce a lower bounding technique for the min max correlation clustering problem and, based on this technique, a combinatorial 4-approximation algorithm for complete graphs. This improves upon the previous best known approximation guarantees of 5, using a linear program formulation (Kalhan et al., 2019), and 40, for a combinatorial algorithm (Davies et al., 2023). We extend this algorithm by a greedy joining heuristic and show empirically that it improves the state of the art in solution quality and runtime on several benchmark datasets.
A Graph Multi-separator Problem for Image Segmentation
Jul 10, 2023Abstract:We propose a novel abstraction of the image segmentation task in the form of a combinatorial optimization problem that we call the multi-separator problem. Feasible solutions indicate for every pixel whether it belongs to a segment or a segment separator, and indicate for pairs of pixels whether or not the pixels belong to the same segment. This is in contrast to the closely related lifted multicut problem where every pixel is associated to a segment and no pixel explicitly represents a separating structure. While the multi-separator problem is NP-hard, we identify two special cases for which it can be solved efficiently. Moreover, we define two local search algorithms for the general case and demonstrate their effectiveness in segmenting simulated volume images of foam cells and filaments.
A Polyhedral Study of Lifted Multicuts
Feb 16, 2022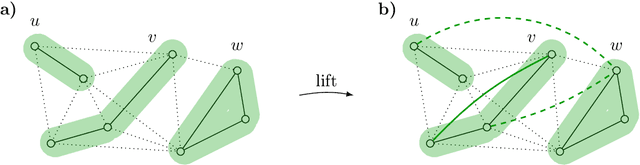
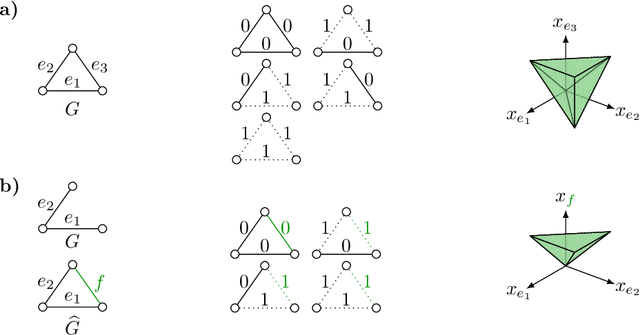
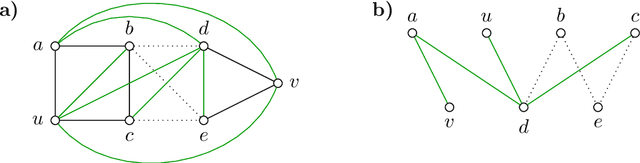
Abstract:Fundamental to many applications in data analysis are the decompositions of a graph, i.e. partitions of the node set into component-inducing subsets. One way of encoding decompositions is by multicuts, the subsets of those edges that straddle distinct components. Recently, a lifting of multicuts from a graph $G = (V, E)$ to an augmented graph $\hat G = (V, E \cup F)$ has been proposed in the field of image analysis, with the goal of obtaining a more expressive characterization of graph decompositions in which it is made explicit also for pairs $F \subseteq \tbinom{V}{2} \setminus E$ of non-neighboring nodes whether these are in the same or distinct components. In this work, we study in detail the polytope in $\mathbb{R}^{E \cup F}$ whose vertices are precisely the characteristic vectors of multicuts of $\hat G$ lifted from $G$, connecting it, in particular, to the rich body of prior work on the clique partitioning and multilinear polytope.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge